中学数学だけでフェルマーの小定理をプログラミングしてみよう:数学×Pythonプログラミング入門
ウォーミングアップとして、中学数学で学ぶ「素数」に関連する「フェルマーの小定理」を題材に、Pythonプログラミングの初歩を振り返る。演算子/変数/関数の使用方法をまとめる。数式をプログラムとして表すための練習問題も用意している。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は本連載の目的を紹介し、実際に数学×Pythonプログラミングを進めていくための準備について説明しました。
今回から、実際に数学を使ってPythonのプログラミングを始めます。最初は、はじめの一歩ということで、自然数や素数に関する定理を取り上げ、それを実際に確かめるためのプログラムを作っていきます。といっても今回はPythonプログラミングの初歩を振り返るウォーミングアップの回なので、多くの人にとっては簡単な内容かと思います。なお、最後に簡単な(ですが、興味深い)練習問題も用意してあるので、ぜひ取り組んでみてください。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。
目標: フェルマーの小定理をプログラミングしてみる
数学が苦手な人でも「素数」については聞き覚えがあると思います。素数とは1より大きく、1と自分自身しか約数を持たない数のことでしたね。つまり、2,3,5,7,11,13……が素数です。素数は中学の初歩的な数学から登場し、素因数分解やそれを利用した約分など、数式を取り扱う上での基本の基本となっています。
もちろん、それだけではありません。例えば、公開鍵方式と呼ばれる暗号化の方法(RSA暗号)などにも広く応用される実用的な「数」でもあります。一方で、無限にある素数の深淵(しんえん)を覗(のぞ)いた者はその人生を狂わせてしまうと言われるほど、数学者にとっては謎が多く、生涯をかけて取り組まれるテーマです。
ここでは深淵を覗くつもりはありませんが、素数に関する簡単な定理を確かめることを通して、Pythonプログラミングに一歩を踏み出していきたいと思います。
さて、ここで取り扱うのはフェルマーの小定理と呼ばれる定理で、RSA暗号にも応用されています。ただし、これは有名なフェルマーの最終定理とは別のもので、以下のような、中学の数学だけで十分理解できるものです(証明はそれほど難しくはありませんが、本筋の話から外れるので、ここでは省略します。興味のある方は「フェルマーの小定理の証明と例題 | 高校数学の美しい物語」などを参照してください)。
自然数aと素数pが互いに素であるとき、aのp−1乗をpで割った余りが1になる
「互いに素(そ)」というのは、1以外の公約数を持たないということです。フェルマーの小定理を数式で表すと以下のようになります。
≡やmodといった記号にはあまりなじみがないかもしれませんが、この式は高校の数学で学ぶ「合同式」と呼ばれるものです。この例であれば「pを法としてap−1は1と合同である」と読みます。ちょっと堅苦しい表現ですが、modは「モッド」または「モジュロ」と読み、「割り算の余り」といった意味になります。「法(ほう)」というのは何らかの整数のことで、ここではpがそれに当たります。
従って、上の式の意味は左辺のap−1をpで割った余りと右辺の1をpで割った余りが必ず等しいということになります。もう少しかみ砕いて言えば、ap−1をpで割った余りが1になるということです。
数学の便利さの一つは、このように説明が長ったらしくなるようなことがらを、(1)式のように簡潔に表現できる点にあります。最初は取っつきにくいかもしれませんが、そのうち数式を見ただけで意味が把握できるようになります。一緒に少しずつ慣れていきましょう。
*1 ちなみに、フェルマーの最終定理は「nが3以上のとき、xn+yn=znを満たす自然数x,y,zは存在しない」というもので、定理そのものは中学の数学でも理解できるものですが、証明は難しく、1995年にアンドリュー・ワイルズによって証明されました。
1. サンプルプログラム(演算子の利用)
では、フェルマーの小定理を具体例で計算してみます。ちょっと大きめの整数aと素数pを使ってみましょう。a=16348039、p=3571とします。これらの値を上で見た(1)式の左辺に当てはめ、計算結果が1になるかどうか確認すればいいですね。以下の式をGoogle Colaboratory(以下Colabと略します)などで入力し、実行してみると結果が確かめられます。動画も用意しておいたので、Google Colabの操作に慣れていない方は参照していただくといいでしょう。
16348039**(3571-1) % 3571
# 出力例:1
「**」はべき乗を求める演算子、「%」は剰余(余り)を求める演算子。
この例では、具体例を1つ試しただけなので、証明にはなっていませんが、確かに余りは1になりました。たった1行の式ですが、これも立派なプログラムです。
【まとめ】演算と演算子
この連載では、Pythonの文法についてサンプルプログラムを理解する上で必要最小限のまとめと数学との関連、留意点のみを整理して掲載することにします。Python文法のより詳細な内容については、連載『Python入門』を参照してください。
では、整理しておきます。演算とは、広い意味での計算のことで、演算子とは演算に使われる記号のことです。まず、四則演算に関する用語と演算子(計算の記号)を整理しておきましょう(表1)。
| 演算の方法 | 別の呼び方 | 数学の演算子 | Pythonの演算子 | 演算の結果 |
|---|---|---|---|---|
| 加法 | 足し算、加算 | + | + | 和 |
| 減法 | 引き算、減算 | - | - | 差 |
| 乗法 | 掛け算、乗算 | × | * | 積 |
| 除法 | 割り算、除算 | ÷ | / | 商 |
足し算と引き算の演算子は数学で使う「+」「-」と同じ。掛け算の演算子は「×」の代わりに「*」を使い、割り算の演算子は「÷」の代わりに「/」を使う。
Pythonでは、答えが整数になる場合でも、割り算を行うと小数点以下が表示されることに注意してください。例えば、4/2の答えは2ではなく2.0となります。
続いて、べき乗、整数商、剰余についてです。これも表にまとめて整理しておきます(表2)。なじみがないものもあるでしょうから、例を示すことにします。
べき乗は同じ数を何回か掛けるという計算ですね。整数商は割り算をしたときの整数部分の答えです。そして剰余はいわゆる「余り」です。まだ小数を習っていない小学校の低学年では、7÷5の答えは「1余り2」のように表しました。「7の中には5が1つある(=整数商)、そして割り切れなくて余った数は2だ(=剰余)」という理屈です。
整数商を求めたり、剰余を求めたりする計算は、周期的な値を分類するのに役立ちます。例えば、ある日が月の第何週にあるかを求めるには整数商を使いますし、何曜日にあるかを求めるには剰余を使います(ただし、1日が何曜日から始まるかを考慮する必要はありますが)*2。
*2 整数の範囲、つまり、負の値を含む範囲だと整数商と剰余が1つに決まりません。元の数をa、割る数をn、整数商をq、剰余をrとすると、a=n×q+rという関係が成り立てばいいので、例えば、-7を3で割る場合、整数商を-3、剰余を2とすることもできますし、整数商を-2、剰余を-1とすることもできます。前者は−7=(−3)×3+2となり、後者は−7=(−3)×2−1となり、どちらも成り立っているからです。
Pythonではどうなるでしょうか。実際にやってみると前者の方法で計算されることが分かります。ちなみに、mathモジュールのfmod関数を使って、以下のように入力すると後者の方法で余りが求められます。
import math
math.fmod(-7,3)
# 出力例:-1.0
これらの演算子の優先度は以下の通りです。優先度の高い演算子から先に計算され、優先度が同じであれば結合方向で示された順序で計算が行われます。これらは数学での計算方法と同じですね。計算の順序を変えたいときには先に計算する部分を()で囲むのも数学と同じです。
| 優先度 | 演算子 | 結合方向 |
|---|---|---|
| 高 | ** | 右から左 |
| | | * / // % | 左から右 |
| 低 | + - | 左から右 |
演算子の優先順位は数学の計算方法と同じ。
2. サンプルプログラム(変数の利用)
前章のリスト1で見たプログラムでは、決まった値の計算しかできません。要するにちょっと便利な電卓のレベルでしかありません。そもそも、この連載の目標は数式をプログラミングできるようになることでした。そのためには、フェルマーの小定理の数式をプログラムとして表す必要があります。そこで、さまざまな値を対象としてこの数式の値を計算できるようにするため、変数を利用してみましょう(動画)。リスト1のコードをリスト2のように書き換えます。
a = 16348039
p = 3571
a**(p-1) % p
# 出力例:1
変数を使うとさまざまな値を使った計算ができる。数式をプログラミングするためには変数は必須。
「=」は数学の「等しい」という意味とは異なり「代入」を表す記号です。従って、「a=16348039」を日本語で読み下すと「変数aに16348039を代入する」ということになります。プログラミング言語の入門書では「変数とは値を入れるための箱のようなもの」という例えで説明されることが多く、代入という言葉も、いままで入っていた値の代わりに新しい値を入れるというイメージですんなりと理解できると思います。
ただし、もう少し進んだプログラムを作ろうとすると、そのイメージだけでは立ち行かなくなることがあります。Pythonにおける変数aへの代入をもう少し正確に言うなら「ある値をaという名前で使えるようにした」といったところです。そのうち、より正確な意味を知る必要が生じてくるので、脳内のイメージを更新できるように「今はとりあえずそう考えておく」と括弧付きで理解しておいてください。
Pythonの変数が数学の変数と大きくことなるところは、Pythonの変数は数文字からなる単語でもいいというところです。数学では変数を1文字で表すので、abcと書けば、a×b×cという意味になります。しかし、Pythonではabcという単語が1つの変数名を表します*3。
*3 Pythonの書き方についてのガイド(PEP8)では、小文字のl(エル)1文字、大文字のI(アイ)1文字、大文字のO(オー)1文字を変数名として使うことは推奨されていません。言うまでもなく、1や0と混同しやすいからです。変数には分かりやすい名前を付けるようにしましょう。
3. サンプルプログラム(関数にする)
前章のリスト2のプログラムで、aの値やpの値を変えればさまざまな場合の例を試せるようになりましたが、まだ大きな問題があります。それは、別の計算をしようとすると、プログラムのコードそのものを書き換えなくてはならないということです。プログラムを書き換えずに、必要に応じて別の値を使って計算できるようにしたいものですね。そのためには関数を定義します。そこで、fermat_littleという名前の関数を定義してみましょう(動画)。
def fermat_little(a, p):
return a**(p-1) % p
fermat_little(16348039, 3571) # 関数を呼び出す
# 出力例:1
fermat_littleという名前の関数を定義する。引数(関数に与える値)はかっこの中にカンマで区切って書く。返り値(関数が答えとして返す値)はreturnの後に書く。
このように、何らかの計算を関数にしておけば、同じ方法で計算を行うときにはその関数を呼び出し、値を与えてやるだけで結果が求められます。以下に関数の書き方を整理しておきましょう。
動画1 演算子/変数/関数を利用するサンプルPythonプログラム
【まとめ】関数の書き方
「関数」は中学や高校の数学でも扱ったので、それなりになじみのある言葉だと思いますが、Pythonの関数も数学の関数と似ていて、何かの値を与えれば、それに対応する答えを返してくれます。
関数の書き方については、言葉で説明するよりは以下のような図で理解した方が分かりやすでしょう。
 図2 関数の書き方
図2 関数の書き方defはdefinition(定義)の略。関数名には分かりやすい名前を自分で付ける。()の中には関数に与えた値を受け取るための変数を書く。これを仮引数(かりひきすう)と呼ぶ。仮引数が複数ある場合はカンマで区切って書く。関数定義の先頭行の最後に「:」を必ず付ける。関数の中にある文はインデント(字下げ)して表す。インデントには2個または4個のスペースを使う。
Pythonでは、関数定義の内容などの範囲を表すためにインデント(字下げ)を使うというのが重要なポイントです。上のリスト3の例では、関数の内容は1行だけですが、もちろん複数行が関数定義の範囲内にある場合はそれらの行を全てインデントします。正しくインデントされていないとエラーになったり、期待した結果が得られなかったりするので注意が必要です。
なお、関数を呼び出すときに与える値のことを「実引数(じつひきすう)」と呼びます。前掲のリスト3であれば、実引数16348039が仮引数aに渡され、実引数3571が仮引数pに渡されます。
4. 最大公約数(G.C.D)を求める
前章で関数の定義方法を学びましたが、一般的によく使われる関数については、あらかじめ利用できるようになっているものが数多くあります。そのような関数を利用する方法を最後に紹介しておきましょう。
例えば、フェルマーの小定理では、aとpは互いに素でなければなりません。つまり、1以外の公約数を持たないので、aとpの最大公約数は1になるはずです。そこで、aとpの最大公約数を求めてみましょう。そのために、私たちは最大公約数を求める関数を自分で作る必要はありません。用意されているgcd関数を利用すればいいのです(リスト4)。なお、gcdはGreatest Common Divisorの略です。
import math
math.gcd(16348039, 3571)
# 出力例:1
gcd関数はmathモジュールに含まれる関数なので、最初にimport mathと書いておく必要がある。math.gcdという名前で呼び出せる。
よく使われる関数は目的や機能によって、(各種ライブラリに含まれる)モジュールと呼ばれるまとまりに分類されています。リスト4で紹介したPython標準ライブラリに含まれるmathモジュールは数学でよく使われる一般的な関数(三角関数や対数関数など)をまとめたものです。モジュールの関数を使うときにはimport文を使ってそのモジュール名を指定しておく必要があります。また、関数を呼び出すときには、モジュール名.関数名の形式でその関数を指定します(簡単な書き方もありますが、またあらためて紹介します)。
では、最後に練習問題です。数学×Pythonプログラミングを楽しんでください。練習問題のプログラム例は動画でも解説しているので、そちらもぜひ参照してください。
動画2 数式を関数で記述する練習問題のプログラム例
練習問題
(1)アンドリカの予想をプログラミングする
アンドリカの予想では、連続した素数をp,qとしたとき、√q−√p < 1が成り立ちます(ただし、まだ証明されてはいません)。pとqを与えて√q−√pを返す関数andricaを作成してみてください。
(ヒント) √を求めるにはmathモジュールに含まれているsqrt関数を使います。
import math
math.sqrt(2)
# 出力例:1.4142135623730951
andrica関数を作成し、例えば、9967と9973を与えて呼び出すと以下のような結果になります。
andrica(9967,9973)
# 出力例:0.03004510184382525
(2)超球の体積を求める
超球の体積を求める以下の公式を使って、半径1のn次元超球の体積を求める関数nsphere_volumeを作成してみてください。以下の式でπは円周率を、Γはガンマ関数と呼ばれる関数(階乗の考え方を実数の範囲にまで拡張した関数)を表し、Rは半径を表します。
超球とはn次元の球のことです。球とは中心から等距離にある点の集まりと考えられます。円は平面つまり二次元の超球と考えられ、球は三次元の超球と考えられます。4次元以上の超球をイメージすることは難しいですが、理論的には中心から等距離にある点の集まりとして考えることはできますね。
(ヒント) πの値やΓ関数はmathモジュールに含まれており、以下のように利用します。
import math
math.pi
# 出力例:3.141592653589793
import math
math.gamma(4)
# 出力例:6.0
以下のような結果になれば正解です。
nsphere_volume(4)
# 出力例:4.934802200544679
nsphere_volume(100)
# 出力例:2.3682021018828293e-40
なお、二次元の超球は円なので、nsphere_volume(2)の結果は、
となり、三次元の超球は球なので、nsphere_volume(3)の結果は、
となります。
練習問題の解答例
(1)アンドリカの予想をプログラミングする
import math
def andrica(p, q):
return math.sqrt(q)-math.sqrt(p)
(2)超球の体積を求める
import math
def nsphere_volume(n):
v = math.pi**(n/2) / math.gamma(n/2+1)
return v
R=1なので、Rn=1です。従って、このプログラムではRの値を指定していません。また、式が少し長くなるので、計算結果をいったんvという変数に代入してから、vの値をreturn文で返しています。
コラム ガンマ関数とは
ガンマ関数は中学・高校の数学では学びませんが、機械学習や統計学などさまざまな分野で広く使われる関数で、階乗の考え方を実数の範囲に広げたものです。グラフにすると図3のようになります。
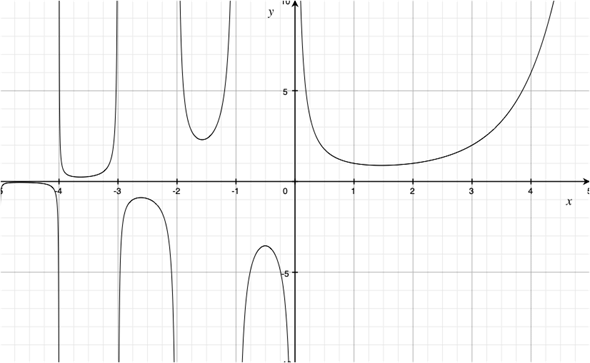 図3 ガンマ関数のグラフ
図3 ガンマ関数のグラフガンマ関数は階乗の考え方を実数の範囲に広げたもの。xが自然数のとき、(x−1)!と等しい。例えば、x=4のときは、(4−1)!=3×2×1=6となる。このグラフはmacOSに付属のGrapherというソフトウェアで描いたもの。
ちなみに、1次元の超球は、線上で中心から等しい距離にある点の集合なので、中心から半径rだけ離れた2点のことになります。半径が1ならこれらの2点間の距離は2になりますね(実際にやってみると、若干の誤差が出ますが、2に近い値になります)。さらに、不思議なことに超球の体積は次元が大きくなるほど0に近づきます。なかなか興味深いですね。
今回はフェルマーの小定理を題材にして、Pythonのプログラムで各種の演算子を使う例を確認し、続いて、変数の利用、関数の作成と利用に進みました。次回は等差数列や等比数列などの数列を例に、リストの表し方や取り扱い方を見ていきます。AI/機械学習などで使われるベクトルデータなどの取り扱いについても理解が深まります。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


 羽山博
羽山博
 表2 べき乗、整数商、剰余の表し方と演算子
表2 べき乗、整数商、剰余の表し方と演算子 図1 関数の働き
図1 関数の働き





