Matplotlibで折れ線グラフ(正規分布など)を描こう:数学×Pythonプログラミング入門(1/3 ページ)
「モデルとデータの可視化」というテーマで関数グラフの描画やヒストグラムや散布図などの各種グラフの取り扱い方を前後編で解説。前編である今回はシグモイド関数のグラフを描く問題を手始めに、さまざまなグラフの描画方法を見ていく。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は、オイラーのγ(ガンマ)と呼ばれる値の近似値を求める例や共分散を求める例、株価の移動平均を求める例などを通して、総和(Σ)や平均、データの個数を求めるための基本的なパターンを見ました。また、制御変数とインデックスの取り扱いについても考えました。
今回のテーマは「ビジュアライズ(可視化、視覚化)」です。内容は、関数のグラフを描画にすることによるモデルの可視化と、収集した数値データや分析結果の可視化という2つに大きく分かれます。そのため、内容量がかなり多くなるので、前編と後編に回を分けることにします。
前編(今回)は、シグモイド関数のグラフを描く例や正規分布の確率密度関数/ベータ分布の確率密度関数を描く例を取り上げます。加えて3Dグラフを作成する方法も紹介します。後編(次回)は、ヒストグラムや散布図、ヒートマップなどを作成し、データの分析に役立てる方法を見ていきます。
今回の練習問題としては、フーリエ級数を利用して矩形波(くけいは)のグラフを描く例、多変数関数による曲面のグラフを描く例を取り上げます。もちろん、全て中学/高校までの数学の知識があれば作成できるプログラムです。グラフ化するデータの準備についてはある程度Pythonの経験がないと難しい部分もありますが、分からない部分については「おまじない」だと思ってサンプルコードをそのまま入力してもらって構いません。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。
目標1: シグモイド関数のグラフを描く
前回までは、数式を使って何らかの計算をすることに重点を置いたプログラムを見てきました。今回と次回は少し気分を変えて、数式やデータを可視化する方法を見ていくこととしましょう。可視化により、数式や数値だけでは分からなかった性質や特徴などが浮かび上がってくることが期待されます。
まずは、ニューラルネットワークの活性化関数として使われるシグモイド関数のグラフを描いてみます。なお、これ以降のサンプルプログラムの実行例については、動画を用意してあるので、プログラムの作成から実行までの流れを確認したい方は、ぜひ視聴してみてください。
動画1 サンプルプログラムの実行例〜シグモイド関数のグラフ/正規分布やベータ分布のグラフ
シグモイド関数は以下の式で表されます。
グラフの描画には、Matplotlibライブラリに含まれるmatplotlib.pyplotモジュールのplot関数を使います。plot関数は折れ線グラフを描画するための関数で、x(横軸)の値のリストとy(縦軸)の値のリストを与えてやれば、簡単にグラフの描画ができます。腕に自信のある方はノーヒントでチャレンジして、2章まで進み、答え合わせをしてみてください。図1のようなグラフが描ければオーケーです(検算も必要ですが、後述します)。
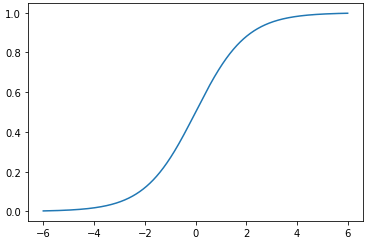 図1 シグモイド関数のグラフ
図1 シグモイド関数のグラフ−6 ≤ x < 6の範囲でグラフを描画した。(1)式の分母が指数で表されていることから、xの値が小さくなれば、exp(-x)が急激に大きくなることが分かる。従って、分母も大きくなり、yの値は0に近くなる。逆に、xの値が大きくなると、exp(-x)が0に近づくので、分母の値が1に近づき、yの値は1に近くなる。グラフの形もそのようになっている。
関数についての数学用語を軽くおさらいしてから次に進みましょう。
- 定義域: 独立変数(x)の取り得る値の範囲
- 値域: 従属変数(y)の取り得る値の範囲
シグモイド関数の定義域は-∞〜+∞で、値域は0〜1です。ただし、横軸を無限に表示することはできないので、上の例(図1)では、定義域を−6 ≤ x < 6としたグラフを描いています。グラフが作成できれば、数式(モデル)がどのような特徴や意味を持つのかが見えてくると思います。なお、独立変数は説明変数、従属変数は目的変数とも呼ばれます。
1. シグモイド関数の定義とグラフの簡単な描き方(基礎知識)
では一歩ずつ進めていきましょう。シグモイド関数のグラフを描くために必要な基礎知識を整理しておきます。何が必要なのかというと、文字通り、
- ステップ1: シグモイド関数を定義する
- ステップ2: グラフを描く
の2つです。というわけで、これらについて確認しておきます。
ステップ1: シグモイド関数を定義する
まず、シグモイド関数の定義です。これは(1)式をそのままPythonの関数として表すだけでいいので簡単ですね。リスト1のコードを穴埋めして作成してみましょう。
from math import exp
def sigmoid(x):
return 1print(sigmoid(-6))
# 出力例:0.0024726231566347743
print(sigmoid(0))
# 出力例:0.5
print(sigmoid(6))
# 出力例:0.9975273768433653
eのべき乗を求めるにはmathモジュールのexp関数を使うとよい。あとは数式の通りにコードを書いていくだけ。
ここで注意すべき点は、import文の書き方がfrom モジュール名 import 関数名となっていることぐらいです(Pythonでは常識レベルの話ですが、この連載では新出事項なので)。import mathと書けば、exp関数はmath.expと書く必要がありますがfrom math import expと書けば、それ以降はexpと書くだけでexp関数が呼び出せます。
答えは以下の通りです。オレンジ色の部分をクリックすると答えが表示されます。
(答え) 1+exp(-x)
関数が定義できたからといって、すぐにグラフを描く作業に移るのではなく、必ず動作確認(検算)しておきましょう。後になってから動作確認すると、誤りがあっても何が原因なのかを探すのが難しくなります。小さなステップで動作確認しておけば、誤りが見つけやすいですから。なお、動作確認を行うときにはコーナーケース(端っこの値や0などの特殊な値)について確認することも忘れずに*1。
*1 検算するといっても正解が分からないことには確認のしようがないですね。正解を知るには、手計算でやってみる、既存の関数があればそれで計算してみる、ExcelやRなど、他のソフトウェアで計算してみるといった方法がありますが、個人的なオススメはWolframAlphaやKeisanなどのウェブサイトの利用です。例えば、WolframAlphaでsigmoid(-6)と入力すると、0.0024726231566347743...という結果だけでなく、さまざまな式の形やグラフなども表示されます。
ステップ2: グラフを描く
続いて、グラフの描き方です。といっても、シグモイド関数のグラフを描くのは、ほんの少しですがハードルが高いので、簡単な例でplot関数の書き方を見ておきましょう。二次関数y=x2ならなじみがあるので、まず、具体的な値を使って考えてみます(数式やリスト内包表記を使った簡潔な書き方についても後のコラムで紹介します)。この関数の値は、x=0,1,2,3,4,5のとき、y=0,1,4,9,16,25となりますね。これらの値をプロットしてみましょう(リスト2)。
import matplotlib.pyplot as plt
x = [0, 1, 2, 3, 4, 5]
y = [0, 1, 4, 9, 16, 25]
plt.plot(x, y)
matplotlib.pyplotモジュールのplot関数にxの値のリストとそれに対するyの値のリストを指定するだけで折れ線グラフが描ける。x, yには、文字列のリストを指定しても構わない。
思った以上に簡単でしたね。もちろん、凝ったグラフを描くにはさまざまな指定が必要になりますが、これが出発点です。実行結果は図2のようになります*2。
*2 Google Colabではセルを実行すると、セル内の最後の式が返す値が自動的に表示されます。上の例だと[<matplotlib.lines.Line2D at 0x7f26911ec7d0>]などの文字列がグラフの上に表示されますが、これはplot関数が返した値(折れ線を表すオブジェクトに関する情報)です。この文字列を表示したくない場合は、plt.show()を最後に追加しておくといいでしょう(show関数は値を返さないので)。
また、実行環境によってはplt.show()を書いておかないとグラフが表示されないことがあります。Google Colabでは、セルのコードが実行されるとグラフは自動的に表示されますが、コードの途中にplt.show()を書くと、作成されたグラフがその時点で表示されます。後で見るリスト7でそういった例を紹介します。
表示されたグラフはちょっとカクカクしていますね。これは、xとyの値が飛び飛びだからです。もう少し値を細かく刻んでいけばスムーズなグラフになるはずです(後でやります)。また、x軸とy軸の目盛りの幅が異なることにも気が付くと思います。これでは二次関数らしく見えません。この例であれば、plot関数の前にplt.figure(figsize=[1.25,6.25])と入力して、x軸の幅とy軸の高さを指定するといいでしょう。x=5のときy=25なので、y軸の高さをx軸の幅の5倍にすれば目盛りの幅が等しくなります。そうすれば、xの値が大きくなるとyの値が急激に増えることが視覚的に表せます。なお、この1.25や6.25という数字の単位はインチです。
コラム リスト内包表記を使ってコードを簡潔に書くには
ステップ2では、二次関数y=x2のグラフを描くのに、具体的な数値を使いましたが、関数を表す数式と繰り返し処理を使うとコードが簡潔になり、汎用性も高まります。for文を使った繰り返し処理で書くなら、リスト3のようになりますが、後(リスト4)に示すリスト内包表記を使うとより簡潔に書けます。
import matplotlib.pyplot as plt
x, y = [], [] # 空のリストを用意しておく
for num in range(6): # numの値は0から5まで
x.append(num) # appendメソッドで要素を追加
y.append(num**2)
plt.plot(x, y)
range関数を使って、numの値を0から5まで(6未満まで)変えながら、x, yのリストに値を追加していく。
リスト内包表記を使うとリスト4のようになります。xについては、リストにしなくてもplot関数の引数に指定できるので、range関数の返り値(rangeオブジェクト)をそのまま代入してあります。
import matplotlib.pyplot as plt
x = range(6)
y = [num**2 for num in x] # リスト内包表現を使う
plt.plot(x, y)
yへの代入を行っている行に注目。xの値を順にnumに代入しながらnum**2の値を求め、それをリスト([]で表される)にしている。
「内包」とは、内側に包み込むといった意味ですね。[]がリストを表すので、その中に包むといったイメージです。[]の中に繰り返し処理を書き、その結果全体をリストにする([]で包む)と考えると分かりやすいでしょう。念のため、図解にもしておきましょう。
 図3 リスト内包表記の書き方と意味
図3 リスト内包表記の書き方と意味for文を使った繰り返し処理でリストを作成することもできるが、リスト内包表記を使うと長いコードもたったの1行で書ける。さらに、この例のnumという変数は他の場所では使わないので、y = [_**2 for _ in x]のように、いちいち名前を付けずに_と書いておくことも多い。
リスト内容表記については、今回はこれ以上登場しませんが、練習問題でまたひょっこりと顔を出します。簡潔なコードを書くのに後々役立つので、ぜひ覚えておいてください。
2. シグモイド関数のグラフを描く(プログラムの作成)
話を本筋に戻しましょう。関数の定義とグラフの描き方が分かったので、本題であるシグモイド関数のグラフに取り組みます。大まかな手順は以下の通りです。
- ステップ1: シグモイド関数sigmoidを定義する ← 既にやった
- ステップ2: xとyの値を用意する: xの値を0.01ずつ増やしながら、対応するyの値を求める
- ステップ3: plot関数にxとyを指定してグラフを描く ← 既にやった
ステップ1: シグモイド関数sigmoidを定義する(実装済みなので省略)
ステップ1のシグモイド関数の定義は1章のステップ1で既にやりました。が、ステップ2との関連で、mathモジュールのexp関数ではなく、numpyモジュールのexp関数を使うことにするので、少しだけ書き換えます。これについてはわずかな書き換えなので、ステップ2でまとめてお話しします。
ステップ3も1章のステップ2で既に見た通りですね。というわけで、新たにやるべきことはステップ2だけです。
ステップ2: xとyの値を用意する: xの値を0.01ずつ増やしながら、対応するyの値を求める
二次関数の例では、xとyのリストがあらかじめ作成されていました。また、xとyの値も整数だったので、特に悩むことはありませんでした。しかし、図4(図1を再掲したもの)を見ると、xの値をかなり細かく刻んでいかないといけないことが分かります。ステップ2で、xの値を0.01ずつ増やしていくとしたのはそのためです。
やるべきことが分かったので、コードを書いていきましょう。ステップ2に当たる処理を関数makedataとして定義することにします。引数にはxの定義域の最小値xminと最大値xmaxを指定すればよさそうですね。ここでは、定義域をxmin以上、xmax未満とします。
ところで、0.01刻みにするにはどうすればいいでしょうか。これまで使ってきたrange関数は連続した整数を返すので、増分値を小数にするのはちょっと面倒です。そこで、科学技術計算を効率よく行うために使われるNumPy(numpyモジュール)のarange関数を使うことにしましょう(リスト5)。arange関数では増分値(刻み幅)に小数を指定できます。なお、arange関数はよく「arrange」と間違えられることがあります。「range」の前に「a」が付いただけと覚えれば間違えないでしょう(「アレンジ」関数ではなく「エーレンジ」関数ですね)。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x)) # NumPyのexp関数を使った
def makedata(xmin, xmax):
x = np.arange(xmin, xmax, 0.01)
y = sigmoid(x) # xはNumPyのarray(配列)なので、対応するyが全て求められる
return x, y
arange関数の3番目の引数が増分値。arange関数はNumPyのarray(配列)という型のデータを返す。yへの代入を行っている文にも注目。numpyモジュールのexp関数を使うと繰り返し処理を使わなくても、xに対応するyの値が全て求められる。yもNumPyのarrayになっている。
NumPyの配列は、これまで使ってきたリストと似ていますが、NumPyの豊富な機能を利用して、はるかに効率のよい便利な操作ができます。
例えば、関数sigmoidの中でmathモジュールのexp関数の代わりに、numpyモジュールのexp関数を使いましたが、exp関数ではブロードキャストと呼ばれる機能により、配列を使った行列の計算が一度にできてしまいます。コードを見ても分かるように、for文を使った繰り返し処理を書く必要がなくなりました。この機能については、また回を改めて(線形代数を取り扱うときに)詳しく説明したいと思います(*3)。
数学では「関数」とは、(厳密に言うと)あるxに対してyの値が1つだけ決まるというものですが、Pythonの関数はカンマで区切って複数の値を返すことができます。ここでは、xとyの2つの値(いずれも配列)を返しています。
*3 以下のコードを使って、簡単な実験をしてみるとmathモジュールの関数とnumpyモジュールの関数の違いがよく分かります。ここでは、sqrt関数を使って試してみます。
import math
x = [1, 2, 3]
math.sqrt(x) # エラーになる
import numpy as np
x = np.array([1, 2, 3]) # NumPyの配列を作る
np.sqrt(x) # 全ての√を求める
# 出力例:array([1. , 1.41421356, 1.73205081])
mathモジュールのsqrt関数は、引数に1つの数値しか指定できないが、numpyモジュールのsqrt関数は、引数に配列(多次元配列)が指定でき、全ての要素を一度に計算できる。返り値として同じサイズの配列が返される。
このような、配列の要素を一度に計算するブロードキャスト機能に対応した関数をユニバーサル関数と呼びます。numpyのユニバーサル関数を利用すると、繰り返し処理を使って要素を一つ一つ処理していく必要がなくなるというわけです。
ちなみに、numpyモジュールのlinspace関数を使うと、増分値ではなく、作成する値の個数が指定できます。例えば、np.linspace(0, 10, 101)とすると、0以上10以下の値が101個に分けて作成されます(「以下」であることに注意が必要ですね。この場合は0.1刻みになります)。0以上10未満を100個に分けて0.1刻みにしたい場合は、末尾(endpoint)を含まないという設定を加えて、np.linspace(0, 10, 100, endpoint=False)とします。
ステップ3: plot関数にxとyを指定してグラフを描く
複数の返り値は、カンマで区切った複数の変数にそれぞれ代入できます。というわけで、リスト7のコードでグラフが描画できます。matplotlib.pyplotモジュールのplot関数には、リストだけでなく、NumPyのarrayもそのまま指定できます。
import matplotlib.pyplot as plt
x, y = makedata(-6, 6)
plt.plot(x, y)
関数makedataで作った配列xと配列yをplot関数に指定してグラフを描く。実行結果は既に見た図1と同じ。
numpyモジュールのarange関数を使えば、小数の増分値が指定できるので、わざわざrange関数を使って繰り返し処理を0.01刻みで行えるように工夫する必要はありませんが、あえてやるとすれば以下のような計算でできます。
- (1)定義域の幅を100倍して、それを制御変数の最大値とする
- (2)制御変数を100で割った値を増分値とする
- (3)定義域の最小値に増分値を足しながら繰り返しを実行する
一般に、10−n刻みであれば、定義域の幅を10n倍したものを制御変数の最大値とし、最小値に制御変数/10nを足しながら繰り返し処理を実行すればいいということが分かります。この方法で関数makedataを書くとリスト8のようになります。
def makedata_for(xmin, xmax): # 関数名は変えておいた
x, y = [], []
limit = (xmax - xmin) * 100 # 定義域を100倍する
for i in range(limit):
x.append(xmin+i/100) # 制御変数を100で割った値を増分値とする。append関数でリストに追加
y.append(sigmoid(x[-1])) # x[-1]はリストxの最後の要素。直前にxに追加した値を関数sigmoidに渡す
return x, y
ロジックを追いかける練習にはなるが、コードは冗長になってしまう。理屈が分かれば、以降は便利な道具(arange関数など)を使った方が楽。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


 羽山博
羽山博

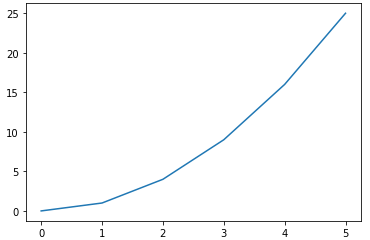 図2 二次関数のグラフ
図2 二次関数のグラフ




