図とコードで必ず分かるニューラルネットワークの逆伝播:ニューラルネットワーク入門
ニューラルネットワークの逆伝播を多数の図とPythonコードから理解しよう。NumPy(線形代数)なしのフルスクラッチで逆伝播の処理を実装してみる。掛け算と足し算の簡単な計算だけで実装できる。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本稿は、ニューラルネットワーク(以下、ニューラルネット)の仕組みや挙動を、数学理論からではなくPythonコードから学ぶことを目標とした連載(基礎編)の第2回です。「難しい高校以降の数学は苦手だけど、コードを読んでロジックを理解するのは得意!」という方にはピッタリの記事です。
前回の第1回では、本連載の目的や特徴を示した後で、「ニューラルネットの訓練(学習)処理を実現するために必要なこと」として、
- ステップ(1)順伝播: forward_prop()関数として実装(前回)
- ステップ(2)逆伝播: back_prop()関数として実装(今回)
- ステップ(3)パラメーター(重みとバイアス)の更新: update_params()関数として実装(次回)。これによりモデルが最適化される
という3大ステップを示しました。前回はこのうちの「ステップ(1)順伝播」まで実装が完了しています。今回はその続きとして、「ステップ(2)逆伝播」までを実装していきます。いよいよ山場ですね。
逆伝播は、数式で見ると複雑怪奇に見えるかもしれません。恐らく式内に文字が多すぎるせいと、式がたくさん出てくるせいだと思います。そんな各所に惑わされて全体像を把握できずに挫折する人が多いのではないかと筆者は考えています。
そこで本稿では、数学理論ではなく、全体図で逆伝播の流れを何度も徹底的に示した上で、その流れをPythonでコーディングしていきます。実際に実装してみると、ニューラルネットを逆に伝播する流れに沿って数式に対応したコードを書いていくだけになります。「意外にも逆伝播は単純で分かりやすい」と思ってもらえたら、本稿は大成功です。タイトルには過剰に「必ず分かる」と入れましたが、筆者自身の目標と意気込みを表しています。読者の皆さんは気軽に、自分でコーディングしている気分で読んでみてください。
※注意点として、本稿では逆伝播のロジックを線形代数なし、つまりNumPyなしで、具体的にはforループでコーディングしていきます。この記事から本連載(基礎編)を読み始めた場合は、その異端ぶりに「むむむ」と驚くかもしれません。このような書き方である理由は第1回で説明していますので、驚いた場合にはぜひご参照ください。
本稿は「線形代数の計算内容を考えるよりも、シンプルな算術計算をそのまま表現したコードを読む方が速い」人向けという想定です。常にforループで書くことを推奨しているわけでなく、ロジックをステップ・バイ・ステップで追いかけて理解するための一手段としてforループを採用しただけです。また、forループで書いたとしても、それは線形代数の中で行われる個々の計算を、コードとして目に見える形で表現したにすぎません。やっている計算は同じです。
さて、前置きはこのくらいにして、逆伝播の話を始めましょう。※なお本稿は、第1回とセットの内容なので、図や掲載コード(「リスト<数字>」と表記)などの番号は前回からの継続となっています。
ステップ2. 逆伝播の実装
それでは、何も見ずにゼロからスクラッチでコードを書くという想定で進めていきます。逆伝播には誤解して嵌(は)まりやすい落とし穴が幾つかある(と筆者は思う)ので、コーディングの前に、逆伝播に対する考え方と注意点を整理しておきます。
ここで質問です。そもそもなぜ、逆伝播をするのでしょうか? 例えば前回説明した訓練時の順伝播の目的は、データなどの数値をニューラルネットに順方向で流すこと(=順伝播)によって「予測すること」と「その途中の計算結果をキャッシュに記録しておくこと」と言えます。実際にforward_prop()関数の戻り値で、y_pred, cached_outs, cached_sumsという3つの計算結果を取得できるように実装しました。では、今回の逆伝播の目的とは何でしょうか。ヒントとして、今回の計算結果(=back_prop()関数の戻り値)を受けて、次回でモデルを最適化するので、最適化そのものではありません。
逆伝播の目的と全体像
逆伝播の目的は、誤差(厳密には予測値に関する損失関数の偏微分係数、後述)などの数値(本稿では誤差情報と呼ぶ)をニューラルネットに逆方向で流すこと(=逆伝播)によって「重みとバイアスの勾配を計算すること」です(図5)。なお勾配(gradient:傾きや傾斜)とは、前回の最後でも簡単に説明したように、各入力/重み/バイアスに関して損失関数を偏微分した計算結果である偏微分係数をまとめた配列(リスト、数学ではベクトル)のことです。
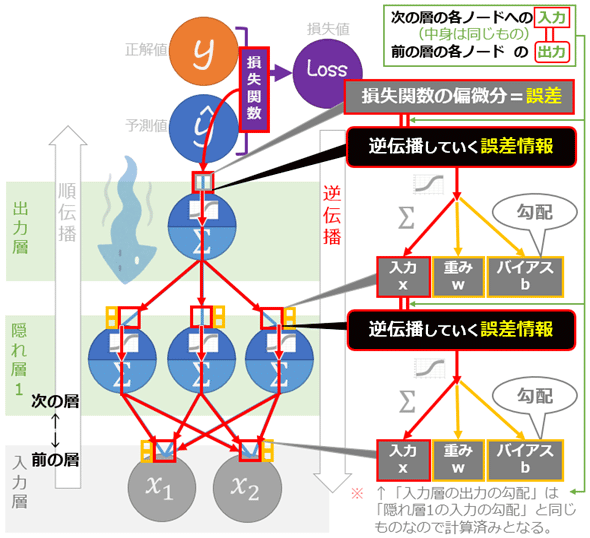 図5 「逆伝播の流れ」のイメージ(左:ネットワーク図、右:対応する処理/数学計算)
図5 「逆伝播の流れ」のイメージ(左:ネットワーク図、右:対応する処理/数学計算)ここでは、赤い矢印の流れで誤差情報が逆に伝播していくことを押さえてほしい。
※逆伝播で逆に進むため「前」と「次」という用語が紛らわしいので注意してほしい。本稿では常に、入力層側を「前の層」、出力層側を「次の層」と呼んでいる。
実際に今回、目的通りに、back_prop()関数から戻り値としてgrads_w, grads_bという2つの勾配(gradients)情報を取得できるようにします(前回のリスト1)。
# 訓練処理
y_pred, cached_outs, cached_sums = forward_prop(cache_mode=True) # (1)
grads_w, grads_b = back_prop(y_true, cached_outs, cached_sums) # (2)
weights, biases = update_params(grads_w, grads_b, LEARNING_RATE) # (3)
と、ここで1つ目の落とし穴があります。順伝播では1種類の計算をするだけでしたが、逆伝播では違うのです。
順伝播の目的である3つの計算結果は、順伝播の計算途中に出た計算結果だったので、実際に行う計算は順伝播の1種類だけでした。それに対して逆伝播の目的である2つの計算結果は、逆伝播自体の計算途中に出た結果ではなく、それに付随して別に出した2つの計算結果なのです。実際に行う計算としては、「各ノードへの入力の勾配(=逆伝播していく誤差情報)」と「各重みの勾配」「各バイアスの勾配」の3種類が必要となります(図6、併せて前掲の図5)。
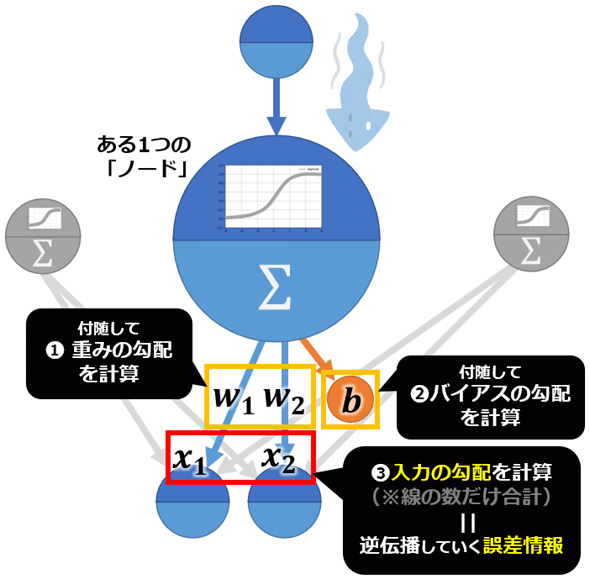 図6 逆伝播では各ノードへの入力/各重み/各バイアスの勾配を計算する
図6 逆伝播では各ノードへの入力/各重み/各バイアスの勾配を計算する※入力の勾配だけ、重みやバイアスの勾配とは計算方法が少し異なる。具体的には、入力(例えばx1)には、多数のエッジ(線)がつながっているので(例えば次の層に3つのノードがあれば3本の線)、その全てのエッジ(例:3本)における入力の偏微分係数を合計する必要がある(後掲の図9でも説明)。
入力の勾配は逆伝播の主役にもかかわらず目立たないので盲点です(※教材によっては隠れ層における重みの勾配を計算する中で暗黙的に算出されています)。なお、逆伝播自体の途中の計算結果である入力の勾配は、最適化の計算には不要なので戻り値として返していません。
以上のことから、逆伝播では非常に数多くの勾配を計算しなければならないということが分かります。具体的には順伝播では、ノードへの入力で(x1×w1+x2×w2+…+xn×wn+b)という重み付き線形和(以下、線形和)の計算が行われますが、逆伝播ではこの中にある変数x1/w1/x2/w2/……/xn/wn/bという大量の変数に関して、損失関数の偏微分係数(=勾配)を計算する必要があるのです。しかもこれを各層のノード数×層の数だけ行うわけですから、本当に大量の計算です。「そりゃ、ディープラーニングは計算に時間がかかって、並列処理に強いGPUが必要になるわ」と思います。
確かに計算すべき勾配はたくさんありますが、前掲の図5(や後掲の図7)を見ると逆伝播する途中の流れはノードごとに共通していますよね。よって、実装コードは「1つのノードにおける逆伝播の処理」という形でまとめることが可能です。そうであればあとは、順伝播の実装と同じようにforループで、層内のノードと各層を繰り返すだけになります。
ということで、逆伝播の全体像や実装の方向性がぼんやりとでも見えてきたでしょうか。他にも解説すべきことはありますが、残りは実装しながら説明します。取りあえず逆伝播の最初、損失関数の微分から実装していきましょう。
損失関数:二乗和誤差
今回は、損失関数として最も基礎的な二乗和誤差(SSE:Sum of Squared Error)を使うことにします。これを前回の活性化関数と同様にPython関数として実装してみます。
二乗和誤差の内容については用語辞典を参考にしてください。二乗和誤差を実装したPython関数はリスト13のように、その偏導関数はリスト14のようになります(※この部分はカンニングOKとさせてください)。
なお上記リンク先の用語辞典では、ミニバッチ学習やバッチ学習におけるデータ数(=バッチサイズ分、nの数)の総和(Σ)を計算する式になっていますが、この総和は次回の最適化処理の中で行います。ちなみに、総和ではなく、平均の方がより良いのですが、それに関する説明は次回行います。今回の損失関数の実装では、データは1件ずつ入ってくる仕様のため、ここでは総和(Σ)を計算する必要はありません。
def sseloss(y_pred, y_true):
return 0.5 * (y_pred - y_true) ** 2
def sseloss_der(y_pred, y_true):
return y_pred - y_true
リスト13やリスト14は、y_pred - y_trueと「予測値から正解値を引く式」になっていますが、逆に「正解値から予測値を引く式」であっても計算結果は同じになります。
※「正解値から予測値を引く式」であっても、二乗和誤差の関数(sseloss_der())を予測値(y_pred)で偏微分した場合、偏導関数はやはりy_pred - y_trueという式になります。なお、人によっては偏導関数を(y_true - y_pred)*(-1)と説明するので違うように見えますが、数式を展開するとやはり同じ式です。
偏導関数の式y_pred - y_trueは、予測値と正解値の「誤差(Error、ズレ)」となっていますね。要するに誤差逆伝播法(error backpropagation)とは、先ほども簡単に触れましたが、この「誤差」の数値(厳密には、予測値に関しての損失関数の偏微分係数)が誤差情報としてニューラルネットワークを「逆」向きに「伝播」していく過程で、本来の目的である各重みと各バイアスの勾配を求める方法というわけです。
ちなみに、分類問題を解くときの、ソフトマックス(Softmax)関数という活性化関数と一緒に使う交差エントロピー誤差(Cross-entropy Loss)という損失関数を偏微分した場合も、偏導関数の式はy_pred - y_trueとなるので、本稿で説明する内容がほぼそのまま通じます。
損失関数の前にあるのは出力層です。出力層や隠れ層における各ノードでの逆伝播の処理は、先ほども「ノードごとに共通」と書きましたが、ワンパターンなので(図7)、処理をまとめることが可能です。
よって次に、出力層と隠れ層における「1つのノードにおける逆伝播の処理」を実装することにしましょう。
1つのノードにおける逆伝播の処理
ところで「逆伝播の目的と全体像」の節で、「勾配とは、各入力/重み/バイアスに関して損失関数を偏微分した計算結果」と説明しました。しかし「損失関数」と「入力や、重み、バイアス」の間には、
- 活性化関数
- 線形和関数
という2つの関数が存在します。つまりこれらが邪魔なので単純には偏微分できません。損失関数と併せて、これらの3つの関数の関係をPythonコード的に表現すると、
Loss( # 損失関数
activation( # 活性化関数(出力層にある j 番目のノード)
summation( # 線形和関数
next_x, # ノードへの入力
w, # 重み
b # バイアス
)
)
)
のようなマトリョーシカ状態になります。こういった入れ子の関数を、数学では合成関数と呼びます。合成関数を微分するときの公式が、あの有名な連鎖律(chain rule:チェーンルール、鎖で連結していくルール)です。※合成関数や連鎖律の数学を知りたい人は、連載『AI・機械学習の数学入門 』の連鎖律の回などを参照してみてください。
連鎖律を使うと、入れ子の合成関数の微分がまるでマジックのように各関数の微分係数の掛け算だけの式に変化します。図8は、各重みに関して損失関数を偏微分する例です。
図8の上部を見ると、逆伝播の流れで後ろから順番に、
「損失関数の偏微分」×「活性化関数の偏微分」×「線形和関数の偏微分」(それぞれの関数への入力値で偏微分)
と掛け算しているだけです。このような非常に簡単な式に置き換えられることが数学で証明されています。本当に美しくてすごい数学公式ですね。
各バイアスや各入力に関して損失関数を偏微分する際も連鎖律の形はほぼ同じです(図9)。
ただし入力については、「今の層(=現在の層、例えば出力層)にある全てのノード」から「前の層(例えば隠れ層1)にあるそれぞれのノード」に逆伝播するので、前の層のノードごとに、今の層の各ノードとつながる全エッジからの各誤差情報(偏微分係数)を合計する必要があります(前掲の図6の説明欄でも言及しました)。ここが2つ目の落とし穴です。
また、「今の層への入力」は「前の層の出力」と同じものなので、逆伝播が層をまたぐときには、「今の層への入力の勾配」をそのまま「前の層の出力の勾配」として引き継げます。具体的には、「今の層における、各入力に関する損失関数の偏微分係数」と「前の層における、各出力に関する損失関数の偏微分係数」が同じものとなります。
最初の「予測値に関する損失関数の偏微分係数」や、各層における各ノードでの「各入力に関する損失関数の偏微分係数」を「逆伝播していく誤差情報」と見なせば、ニューラルネットの後ろから1層1層さかのぼって計算していくときの、各層における各ノードでの計算は、
「逆伝播していく誤差情報」×「活性化関数の偏微分」×「線形和関数の偏微分」
という掛け算に共通化できます(図10)。
これなら、出力層から隠れ層まで全てワンパターンで実装できますね。具体的にそのパターンは、以下の4工程になります(図11)。
- (1)逆伝播していく誤差情報
- (2)活性化関数を偏微分
- (3)線形和を重み/バイアス/入力で偏微分
- (4)各重み/バイアス/各入力の勾配を計算
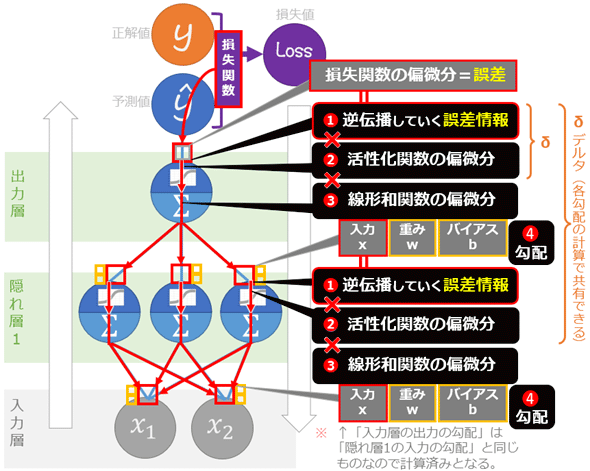 図11 「逆伝播の流れ」の実装内容
図11 「逆伝播の流れ」の実装内容最初に示した「図5 『逆伝播の流れ』のイメージ」に、これから実装するパターンである(1)〜(4)の4工程を書き加えたもの。
各入力/重み/バイアスに関して損失関数を偏微分する際、途中までの計算は同じなのでデルタ δ という値で共有できる(前掲の図9参照)。詳しくはこれからの実装で示す。
以上で実装に必要な事前知識はそろったので、いよいよそれぞれ実装していきましょう。実装中に使う仮のモデルのアーキテクチャーについては、前回で定義した「モデルの定義と、仮の訓練データ」と同様です(入力層のノードが2個、隠れ層のノードが3個、出力層のノードが1個で、活性化関数は隠れ層がシグモイド関数、出力層が恒等関数です)。
(1)逆伝播していく誤差情報
出力層と隠れ層で処理が異なります。出力層では「予測値に関する損失関数の偏微分係数」(前掲のリスト14で実装したsseloss_der()関数)を計算し、隠れ層では「次の層への各入力(=今の層の各出力)に関する損失関数の偏微分係数」(後述のリスト21でgrads_x変数に格納される予定)を取得し、それを「逆伝播していく誤差情報」(back_error変数)として保持します(リスト15)。
# 取りあえず仮で、変数を定義して、コードが実行できるようにしておく
layer_i = 2 # 2:出力層、1:隠れ層1、0:入力層
layer_max_i = 2 # 最後の層(=出力層)のインデックス
is_output_layer = (layer_i == layer_max_i) # 出力層か(True)、隠れ層か(False)
# 入力層/隠れ層1/出力層にある各ノードの(活性化関数の)出力値
cached_outs = [[0.05, 0.1], [0.5, 0.5, 0.5], [0.0]]
y_true = [1.0] # 正解値
grads_x = [] # 入力の勾配
# ---ここまでは仮の実装。ここからが必要な実装---
if is_output_layer:
# 出力層(損失関数の偏微分係数)
back_error = [] # 逆伝播していく誤差情報
y_pred = cached_outs[layer_i]
for output, target in zip(y_pred, y_true):
loss_der = sseloss_der(output, target) # 誤差情報
back_error.append(loss_der)
else:
# 隠れ層(次の層への入力の偏微分係数)
back_error = grads_x[-1] # 最後に追加された入力の勾配
y_trueなどをforループで回しているのは、出力層のノードが2個以上ある場合への対応です。仮のモデルは、出力層のノードが1個なので、実質的にはループして個々に処理する必要はありません。一方、本稿の最後に示す実行例では、出力層のノードが2個なのでループが必要です。
※(1)は層ごとにまとめての処理でした。以下からの(2)〜(4)はノードごとの処理になります。
(2)活性化関数を偏微分
活性化関数の偏微分は、前回定義した活性化関数の導関数を呼び出すだけです。出力層では「恒等関数の導関数」(前回のリスト9で実装したidentity_der()関数)を、隠れ層では「シグモイド関数の導関数」(前回のリスト7で実装したsigmoid_der()関数)を呼び出し、「活性化関数の偏微分係数」(active_der変数)を取得します(リスト16)。
# 取りあえず仮で、変数を定義して、コードが実行できるようにしておく
SKIP_INPUT_LAYER = 1 # 入力層を飛ばす
cached_sums = [[0.0, 0.0, 0.0], [0.0]] # 隠れ層1/出力層(※入力層はない)
node_sum = cached_sums[layer_max_i - SKIP_INPUT_LAYER] # 出力層
# ---ここまでは仮の実装。ここからが必要な実装---
if is_output_layer:
# 出力層(恒等関数の微分)
active_der = identity_der(node_sum)
else:
# 隠れ層(シグモイド関数の微分)
active_der = sigmoid_der(node_sum)
(3)線形和を重み/バイアス/入力で偏微分
線形和関数を重み/バイアス/入力で偏微分します。線形和の偏微分も、前回定義した重み付き線形和の偏導関数(前回のリスト5で実装したsum_der()関数)を呼び出すだけです。前掲の図6のところでも説明したように、各重み(引数with_respect_to='w')/各バイアス(引数with_respect_to='b')/各入力(引数with_respect_to='x')の3種類それぞれで呼び出す必要があります(リスト17)。ここが1つ目の落とし穴でした。その結果、3種類の「線形和関数の偏微分係数」(sum_der_w/sum_der_b/sum_der_x変数)が取得できます。
# 取りあえず仮で、変数を定義して、コードが実行できるようにしておく
PREV_LAYER = 1 # 前の層を指定するため
node_i = 0 # ノード番号
# 重みとバイアスの初期値
weights = [
[[0.0, 0.0], [0.0, 0.0], [0.0, 0.0]], # 入力層→隠れ層1
[[0.0, 0.0, 0.0]] # 隠れ層1→出力層
]
biases = [
[0.0, 0.0, 0.0], # 隠れ層1
[0.0] # 出力層
]
# 入力層/隠れ層1/出力層にある各ノードの(活性化関数の)出力値
cached_outs = [[0.05, 0.1], [0.5, 0.5, 0.5], [0.0]]
# ---ここまでは仮の実装。ここからが必要な実装---
w = weights[layer_i - SKIP_INPUT_LAYER][node_i]
b = biases[layer_i - SKIP_INPUT_LAYER][node_i]
x = cached_outs[layer_i - PREV_LAYER] # 前の層の出力(out)=今の層への入力(x)
sum_der_w = sum_der(x, w, b, with_respect_to='w')
sum_der_b = sum_der(x, w, b, with_respect_to='b')
sum_der_x = sum_der(x, w, b, with_respect_to='x')
以上で、(1)〜(3)までの実装が完了しました(図12)。逆伝播の順に3段階で偏微分しただけで簡単ですね。
あとは算出した各偏微分係数で勾配を計算します。
(4)各重み/バイアス/各入力の勾配を計算
まずは共通の計算部分であるデルタ(delta変数)を計算します。「逆伝播していく誤差情報」と「活性化関数の偏微分係数」を掛け算するだけです(リスト18)。
delta = back_error[node_i] * active_der
デルタについては、前掲の図11に記載されていましたが、図13にその部分を抜粋して再掲しておきます。
次にバイアスの勾配(grad_b変数)を計算します。「デルタ」と「線形和関数の偏微分係数」を掛け算するだけです(リスト19)。バイアスから計算するのは、バイアスが1つしかなく、エッジ(線)がない、つまり「前の層のノード」と関係がないため(再掲する図9にも記載)、計算が楽だからです。
# 取りあえず仮で、変数を定義して、コードが実行できるようにしておく
layer_grads_b = [] # 層ごとの、バイアス勾配のリスト
# ---ここまでは仮の実装。ここからが必要な実装---
# バイアスは1つだけ
grad_b = delta * sum_der_b
layer_grads_b.append(grad_b)
最後に各重みの勾配(grad_w変数)と各入力の勾配(grad_x変数)を計算します(リスト20)。
# 取りあえず仮で、変数を定義して、コードが実行できるようにしておく
layer_grads_w = [] # 層ごとの、重み勾配のリスト
layer_grads_x = [] # 層ごとの、入力勾配のリスト
# ---ここまでは仮の実装。ここからが必要な実装---
# 重みと入力は前の層のノードの数だけある
node_grads_w = []
for x_i, (each_dw, each_dx) in enumerate(zip(sum_der_w, sum_der_x)):
# 重みは個別に取得する
grad_w = delta * each_dw
node_grads_w.append(grad_w)
# 入力は各ノードから前のノードに接続する全ての入力を合計する
# (※重み視点と入力視点ではエッジの並び方が違うので注意)
grad_x = delta * each_dx
if node_i == 0:
# 最初に、入力の勾配を作成
layer_grads_x.append(grad_x)
else:
# その後は、その入力の勾配に合計していく
layer_grads_x[x_i] += grad_x
layer_grads_w.append(node_grads_w)
forループを使うことで、前の層にあるノードごと(=エッジごと)に処理しています。「デルタ」と「線形和関数の偏微分係数」を掛け算するだけの計算方法は、バイアスの場合と同じですね。
重みの勾配は単純に、前の層にあるノードごと(=エッジごと)に勾配を計算して、今の層にあるノードごとに保持し(node_grads_w変数)、最後にそれを層ごとのリストにまとめています(layer_grads_w変数)。
入力の勾配は、前の層にあるノードごと(=エッジごと)に勾配を計算して、「今の層からのエッジ」を全て合計していっています(layer_grads_x変数)。合計が必要な点が2つ目の落とし穴でしたね。
以上で、主要な実装は完了しました。(1)〜(4)の実装内容は前掲の図9に書いた通りなので、もし分からない部分があったなら、先ほど再掲した図9を再確認してみてください。
あとは、全体をまとめ上げるだけです。
逆伝播の処理全体の実装
順伝播の実装と同じような説明内容になりますが、ニューラルネットは、層があり、その中に複数のノードが存在するという構造ですので、
- 逆順に各層を1つずつ処理するforループと
- 層の中のノードを1つずつ処理するforループの2段階構造が必要で
- その中に「1つのノードにおける逆伝播の処理」を記述
- 層の中のノードを1つずつ処理するforループの2段階構造が必要で
すればよいわけです。
この考えに沿って、逆伝播の処理全体を行うback_prop()関数を実装してみたのがリスト21です。2つのforループと、既に説明済みの(1)〜(4)の実装(特に太字で示した8行)に注目してください。それら以外のコードは、勾配を多次元リストにまとめるためのこまごました処理なので、読み飛ばしても構いません。
def back_prop(layers, weights, biases, y_true, cached_outs, cached_sums):
"""
逆伝播を行う関数。
- 引数:
(layers, weights, biases): モデルを指定する。
y_true: 正解値(出力層のノードが複数ある場合もあるのでリスト値)。
cached_outs: 順伝播で記録した活性化関数の出力値。予測値を含む。
cached_sums: 順伝播で記録した線形和(Σ)値。
- 戻り値:
重みの勾配とバイアスの勾配を返す。
"""
# ネットワーク全体で勾配を保持するためのリスト
grads_w =[] # 重みの勾配
grads_b = [] # バイアスの勾配
grads_x = [] # 入力の勾配
layer_count = len(layers)
layer_max_i = layer_count-1
SKIP_INPUT_LAYER = 1
PREV_LAYER = 1
rng = range(SKIP_INPUT_LAYER, layer_count) # 入力層以外の層インデックス
for layer_i in reversed(rng): # 各層を逆順に処理
is_output_layer = (layer_i == layer_max_i)
# 層ごとで勾配を保持するためのリスト
layer_grads_w = []
layer_grads_b = []
layer_grads_x = []
# (1)逆伝播していく誤差情報
if is_output_layer:
# 出力層(損失関数の偏微分係数)
back_error = [] # 逆伝播していく誤差情報
y_pred = cached_outs[layer_i]
for output, target in zip(y_pred, y_true):
loss_der = sseloss_der(output, target) # 誤差情報
back_error.append(loss_der)
else:
# 隠れ層(次の層への入力の偏微分係数)
back_error = grads_x[-1] # 最後に追加された入力の勾配
node_sums = cached_sums[layer_i - SKIP_INPUT_LAYER]
for node_i, node_sum in enumerate(node_sums): # 各ノードを処理
# (2)活性化関数を偏微分
if is_output_layer:
# 出力層(恒等関数の微分)
active_der = identity_der(node_sum)
else:
# 隠れ層(シグモイド関数の微分)
active_der = sigmoid_der(node_sum)
# (3)線形和を重み/バイアス/入力で偏微分
w = weights[layer_i - SKIP_INPUT_LAYER][node_i]
b = biases[layer_i - SKIP_INPUT_LAYER][node_i]
x = cached_outs[layer_i - PREV_LAYER] # 前の層の出力=今の層への入力
sum_der_w = sum_der(x, w, b, with_respect_to='w')
sum_der_b = sum_der(x, w, b, with_respect_to='b')
sum_der_x = sum_der(x, w, b, with_respect_to='x')
# (4)各重み/バイアス/各入力の勾配を計算
delta = back_error[node_i] * active_der
# バイアスは1つだけ
grad_b = delta * sum_der_b
layer_grads_b.append(grad_b)
# 重みと入力は前の層のノードの数だけある
node_grads_w = []
for x_i, (each_dw, each_dx) in enumerate(zip(sum_der_w, sum_der_x)):
# 重みは個別に取得する
grad_w = delta * each_dw
node_grads_w.append(grad_w)
# 入力は各ノードから前のノードに接続する全ての入力を合計する
# (※重み視点と入力視点ではエッジの並び方が違うので注意)
grad_x = delta * each_dx
if node_i == 0:
# 最初に、入力の勾配を作成
layer_grads_x.append(grad_x)
else:
# その後は、その入力の勾配に合計していく
layer_grads_x[x_i] += grad_x
layer_grads_w.append(node_grads_w)
# 層ごとの勾配を、ネットワーク全体用のリストに格納
grads_w.append(layer_grads_w)
grads_b.append(layer_grads_b)
grads_x.append(layer_grads_x)
# 保持しておいた各勾配(※逆順で追加したので反転が必要)を戻り値で返す
grads_w.reverse()
grads_b.reverse()
return (grads_w, grads_b) # grads_xは最適化で不要なので返していない
コード中にもコメントを入れていますが、(1)〜(4)は説明済みなのでそれ以外で気を付けてほしいポイントを以下でも触れておきます。
まず、前掲の図13などでも分かるように、入力層は処理不要なのでforループで回さないようにしています。
次に、「今の層における入力の勾配」を計算した後(grads_x.append(layer_grads_x))、次の層のループでback_error = grads_x[-1]というコードにより「逆伝播していく誤差情報」として使っています。ここが層から層へ誤差情報が逆伝播していっているところに相当しますね。
最後に、重みの勾配(grads_w)やバイアスの勾配(grads_b)は逆順に追加されているので、戻り値として返す直前でreverse()メソッドにより順序を反転させて正順に変えています(reverse()メソッドは、リストの内容をインプレースで逆順に並べ替えるので、結果を自分に代入していない点に注意してください)。
以上でback_prop()関数が完成したので、試しに実行してみましょう。
逆伝播の実行例
リスト22のようなコードを書けば、順伝播から逆伝播までを続けて実行できます。
x = [0.05, 0.1]
layers = [2, 2, 2]
weights = [
[[0.15, 0.2], [0.25, 0.3]],
[[0.4, 0.45], [0.5,0.55]]
]
biases = [[0.35, 0.35], [0.6, 0.6]]
model = (layers, weights, biases)
y_true = [0.01, 0.99]
# (1)順伝播の実行例
y_pred, cached_outs, cached_sums = forward_prop(*model, x, cache_mode=True)
print(f'y_pred={y_pred}')
print(f'cached_outs={cached_outs}')
print(f'cached_sums={cached_sums}')
# 出力例:
# y_pred=[1.10590596705977, 1.2249214040964653]
# cached_outs=[[0.05, 0.1], [0.5932699921071872, 0.596884378259767], [1.10590596705977, 1.2249214040964653]]
# cached_sums=[[0.3775, 0.39249999999999996], [1.10590596705977, 1.2249214040964653]]
# (2)逆伝播の実行例
grads_w, grads_b = back_prop(*model, y_true, cached_outs, cached_sums)
print(f'grads_w={grads_w}')
print(f'grads_b={grads_b}')
# 出力例:
# grads_w=[[[0.006706025259285303, 0.013412050518570607], [0.007487461943833829, 0.014974923887667657]], [[0.6501681244277691, 0.6541291517796395], [0.13937181955411934, 0.1402209162240302]]]
# grads_b=[[0.13412050518570606, 0.14974923887667657], [1.09590596705977, 0.23492140409646534]]
リスト22のモデルの層構成や重みなどは、手計算で逆伝播などを計算している記事と同じ数値にしてみました。ただし上記のリンク先の記事では、全ての活性化関数がシグモイド関数になっています。よって、この記事の手計算と同じ結果にするには、前回のリスト10のidentity(node_sum)をsigmoid(node_sum)に、今回のリスト21のidentity_der(node_sum)をsigmoid_der(node_sum)にする必要があります。これを行った上で実行した結果、重み勾配の最初の値が0.00043856773447434685となりました。記事では0.000438568と計算されているので、確かに正しく計算できていることが確認できました。
今回は、本連載(基礎編)の山場である逆伝播を実装しました。逆伝播の数式を見ると複雑で難しく感じていたかもしれません。しかし、実際にコードを書いてみると、意外にも単純だと感じられたのではないでしょうか。連鎖律のおかげで、後ろから素直に掛け算していくだけですので。
また今回の記事で多用した図解は実はほぼ数学内容の解説でした。それを数学ではない雰囲気で説明しただけです。きちんと逆伝播の数学を学びたい場合は、まずはYouTube動画であれば、「ヨビノリ:絶対に理解させる誤差逆伝播法【深層学習】」がお勧めです。記事であれば、英語ですが先ほどの手計算の記事「A Step by Step Backpropagation Example」が分かりやすくてお勧めです。なお、この動画や記事の説明と本稿では、入力の勾配を計算するタイミングが少し違います(具体的には隠れ層における重みの勾配を計算するタイミングで算出しており、「入力の勾配」のような呼び方はしていません)。が、全体的な計算内容は同じです。
さて次回は、基礎編の最終回となる最適化について説明します。最適化の実装は簡単なので、ニューラルネット全体の実装も完了させる予定です。サンプル実行として回帰問題を取り上げる予定です。お楽しみに。
Copyright© Digital Advantage Corp. All Rights Reserved.



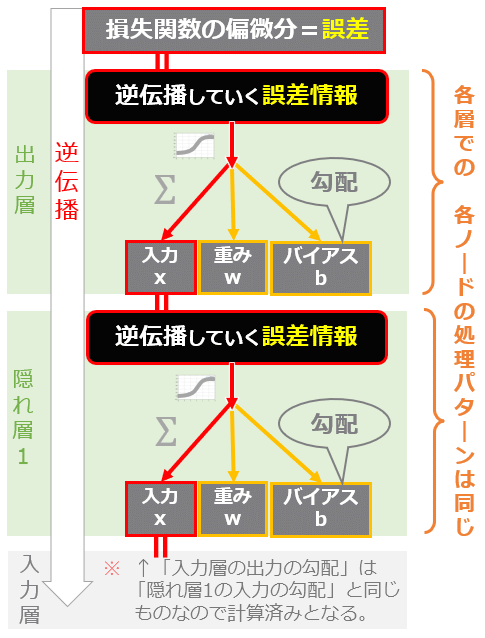 図7 各ノードでの逆伝播の処理はワンパターン
図7 各ノードでの逆伝播の処理はワンパターン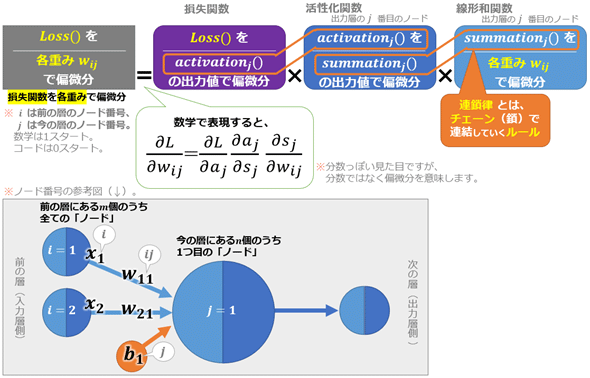
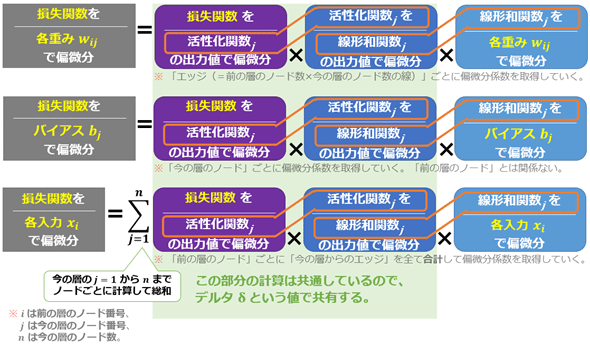
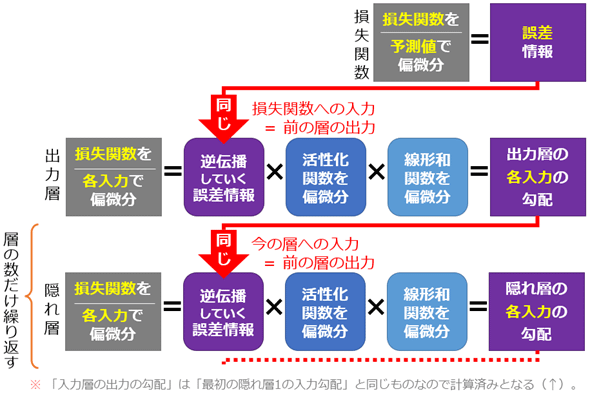
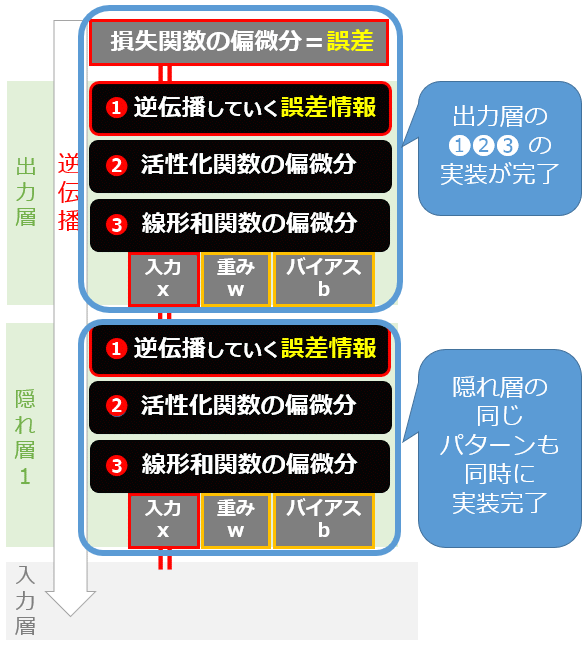 図12 「逆伝播していく誤差情報」「活性化関数を偏微分」「線形和を偏微分」まで実装完了
図12 「逆伝播していく誤差情報」「活性化関数を偏微分」「線形和を偏微分」まで実装完了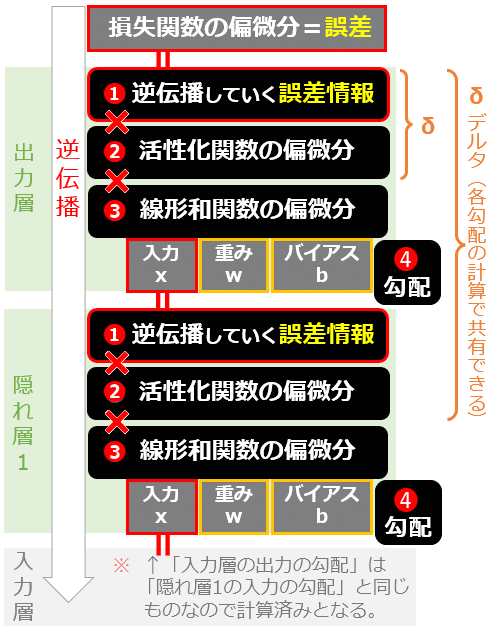 図13 デルタ(delta、
図13 デルタ(delta、



