Pythonでニューラルネットワークを書いてみよう:ニューラルネットワーク入門
ニューラルネットワークの仕組みや挙動を、数学理論からではなく、Pythonコードから理解しよう。まずはニューラルネットワーク(Deep Neural Network)の順伝播をフルスクラッチで実装する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本連載(基礎編)の目的
スクラッチ(=他者が書いたソースコードを見たりライブラリーを使ったりせずに、何もないゼロの状態からコードを記述すること)でディープラーニングやニューラルネットワーク(DNN:Deep Neural Network、以下では「ニューラルネット」と表記)を実装して学ぶ系の書籍や動画講座、記事はたくさんあると思います。それらで学んだ際に、「誤差逆伝播」(バックプロパゲーション)のところで挫折して、そこはスルーしている人は少なくないのではないでしょうか。個々の数式や計算自体を理解していても、何となく全体像がつかめずに、
- 「誤差逆伝播を完全に理解している」
- 「そらでコードが書ける」
- 「人に説明できる」
と自信を持って言えない人も多いのではないかと思います。
本連載(基礎編)はそういった人に向けた記事になります。この記事はニューラルネットの仕組みを、数学理論からではなくPythonコードから学ぶことを狙っています。「難しい高校以降の数学は苦手だけど、コードなら読めるぜ!」という方にはピッタリの記事です。ぜひ写経ではなく何も見ずにそらでコードが書けるようになりましょう。
本連載(基礎編)の特徴
本連載(基礎編)の特徴は、線形代数(linear algebra、行列演算)を使わないことです。つまりNumPyを使いません。基本的に掛け算や足し算などの中学までの数学のみで、ニューラルネットのロジックをコーディングしていきます(※高校レベルの数学に対応するコードも少し出てきますが計算はしないので、中学数学レベルの知識で大丈夫です)。
線形代数を使うと確かにコードが短くなり効率的ですし、シンプルなので何となく理解できた気になります。しかし仕組みとなるロジックを理解するためには、ニューラルネットの順伝播や逆伝播での「数値の流れ」を逐一追っていく必要があると思います。その際には、線形代数の中に隠された多数の「掛け算と足し算の数式」を頭の中や紙の上で展開させつつ追う必要があります。例えばu=Wx+bという線形代数の式には、u=(x1×w1+x2×w2+…+xn×wn+b)×ノード数分の数式が隠れているので、そのロジックを理解するには、これを展開する必要があるわけです。このことが、誤差逆伝播を理解する際の妨げの一因になっていると筆者は感じました。
そうであるなら、最初から線形代数に隠されている数式を展開した状態で実装してしまえばよい、というのが本連載(基礎編)の着想です。全ての数式がコードに書き出されているので、コードを読むだけでロジックを順々に追っていけるというわけです(図1)。頭の中や紙の上で数式を展開する必要はありません。
とはいえ、「線形代数の式を個々の式にバラすと大量のコードになってしまうよね?」という問題があります。確かにその通りですが、線形代数で処理する部分は「繰り返しの数式」になっているので、「Pythonの繰り返し処理であるforループ」に置き換えることが可能です。例えば線形代数の式にあったWxという部分は、図1の赤枠のように展開でき、これをforループで短くまとめられます。それでも冗長ですが、筆者の感想では、堪えられるコード量かなと思います(※手元でコメント行と空行を外して行数を計算すると、線形代数のコード例で全部で約100行でしたが、forループのコード例では全部で約180行でした。人によっては、数学で悩む100行のコードよりも、数学で悩まない180行のコードの方が堪えられますよね)。この点からも「線形代数の計算内容を考えるよりも、シンプルな算術計算をそのまま表現したコードを読む方が速い」という人向けの記事です。
※なお、ニューラルネットで使う数学には、線形代数の他、偏微分(partial differential)があります。具体的には活性化関数や損失関数の微分を行う必要があります。しかし本連載では、損失関数の微分を行うための導関数をそのままコードとして記載することで、微分の計算は取り上げません。例えば活性化関数のシグモイド関数の導関数のコードはこちらの用語辞典に記載されているものを使います(※この部分はカンニングOKとさせてください)。どうしてそういう式とコードになるかが気になる人は、連載『AI・機械学習の数学入門 』の偏微分の回などを参照してみてください。
※ニューラルネットを学ぶこと自体が初めてという方は、事前に『ニューラルネットワークの仕組みの理解×初めての実装(前編/中編/後編)』に目を通しておくと、基礎用語と概念、意味や特性が押さえられるので、より本連載が理解できると思います。
本連載は、まず「基礎編」として、
という3本の記事を公開予定です。その後に、線形代数を使う実装や、各機能のより細かい実装の続編を検討しています。
前置きと意気込みが長くなってしまいましたが、いよいよ本編に入ります。基礎編(今回〜次々回)の内容に対応するノートブックは下記のリンク先で実行/入手できます(※Google Colabのインデントはスペース2個の設定ですが、本連載はスペース4個で記述したので、本連載のコードをコピー&ペーストする場合はスペース数を4個に切り替えてください)。本稿では、コードを短くするため、ほとんどの関数のdocstring(ドキュメントコメント)を省略しましたが、ノートブック側には含めています。
ニューラルネットワークの図
まず基本的なニューラルネット(この例では、入力層:2、隠れ層:3、出力層:1)の図を確認しておきましょう(図2)。簡単にポイントを説明しておくと、ニューラルネットで予測するときの処理が順伝播(forward propagation)で、訓練(=学習)するときの処理(詳細後述)の中で要となるのが逆伝播(バックプロパゲーション:backpropagation)ですね。なお伝播(でんぱ)とは、入力などの数値が、ネットワーク内の結合線(コネクション、リンク、本連載ではエッジと呼ぶ)を通じて次の層もしくは前の層のニューロン(ユニット、本連載ではノードと呼ぶ)に伝わっていくことです。
通常は図2の左のように横に描きますが、本連載では上から順番に説明文を入れやすいよう、(基本的に)図2の右のように縦に描くことにしました。入力層を下にしているので、順伝播が下から上に進むことになります。本連載で一番重要なテーマが「逆伝播」なので、上から下に向かって読める図にしました。
訓練(学習)処理全体の実装
それではさっそく、何も見ずにゼロからコードを書いていくという想定で、コードを書き始めましょう。フルスクラッチ実装のコツは、最初から完璧なコードを書かないことです。メインとなる小さな動く部分を作って、それを徐々に膨らませていきます。深層「学習」のメインは、ニューラルネットの「訓練」処理ですよね。ここから書いていきます(リスト1)。
※なお基礎編(今回〜次々回)のニューラルネットの実装では、Pythonのクラスは使わずに、全てPythonの関数とforループで書いていきます。線形代数(NumPy)を使わないので、データは1件ずつ(=表形式データの1行ずつ)処理します。データをまとめて処理するミニバッチ学習などの各学習方法への対応は「モデルの最適化」に関係する部分なので、次々回(後編)であらためて説明します。
# 取りあえず仮で、空の関数を定義して、コードが実行できるようにしておく
def forward_prop(cache_mode=False):
" 順伝播を行う関数。"
return None, None, None
y_true = [1.0] # 正解値
def back_prop(y_true, cached_outs, cached_sums):
" 逆伝播を行う関数。"
return None, None
LEARNING_RATE = 0.1 # 学習率(lr)
def update_params(grads_w, grads_b, lr=0.1):
" パラメーター(重みとバイアス)を更新する関数。"
return None, None
# ---ここまでは仮の実装。ここからが必要な実装---
# 訓練処理
y_pred, cached_outs, cached_sums = forward_prop(cache_mode=True) # (1)
grads_w, grads_b = back_prop(y_true, cached_outs, cached_sums) # (2)
weights, biases = update_params(grads_w, grads_b, LEARNING_RATE) # (3)
print(f'予測値:{y_pred}') # 予測値: None
print(f'正解値:{y_true}') # 正解値: [1.0]
ニューラルネットの訓練に必要なことは、リスト1の通り、
の3つだけです(図3)。それぞれの関数の戻り値が、次の関数の引数に渡されて受け継がれていますね。各戻り値や引数の詳細は、それぞれの関数の実装時にそのdocstring(ドキュメントコメント)などであらためて説明します。
それでは、各関数を1つずつ実装していきます。が、関数が正常に動作するかを検証するために、仮のニューラルネットのアーキテクチャーを定義してモデルとして生成しておき、サンプルの訓練データも作っておきたいと思います。
モデルの定義と、仮の訓練データ
図2や図3で示したのと同じ、入力層のノードが2個、隠れ層のノードが3個、出力層のノードが1個のモデル(model変数)を定義しましょう。基礎編(今回〜次々回)はクラスを使わないので、タプルで表現しようと思います。層構造(layers変数)や重み(weights変数)やバイアス(biases変数)はPythonのリストで表現します。1件分の訓練データ(x変数)も1次元のリストで表現します(リスト2)。
# ニューラルネットワークは3層構成
layers = [
2, # 入力層の入力(特徴量)の数
3, # 隠れ層1のノード(ニューロン)の数
1] # 出力層のノードの数
# 重みとバイアスの初期値
weights = [
[[0.0, 0.0], [0.0, 0.0], [0.0, 0.0]], # 入力層→隠れ層1
[[0.0, 0.0, 0.0]] # 隠れ層1→出力層
]
biases = [
[0.0, 0.0, 0.0], # 隠れ層1
[0.0] # 出力層
]
# モデルを定義
model = (layers, weights, biases)
# 仮の訓練データ(1件分)を準備
x = [0.05, 0.1] # x_1とx_2の2つの特徴量
重みの初期値は意外に重要なのですが、ここでは単純に全て0としました。本来であれば、「前の層のノード数×今の層のノード数」でエッジ(リンク)を自動生成するなどして、必要な数と多次元配列構造の重みも自動生成すべきですが、コードを短くするためにハードコーディングしました(余裕のある方は、ここで自動生成の処理を自分で実装してみると、よりコーディングを楽しめるかもしれません)。
ステップ1. 順伝播の実装
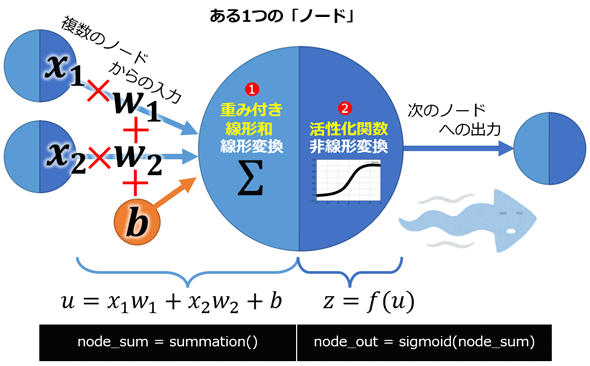
1つのノードにおける順伝播の処理
ニューラルネットの最小単位はノードです。まずは1つのノードにおける順伝播の処理をコーディングしましょう(リスト3)。入力層は何もしませんので、隠れ層と出力層におけるノードの共通処理を記述します。x変数は、リスト2で記述した訓練データです。
# 取りあえず仮で、空の関数を定義して、コードが実行できるようにしておく
def summation(x,weights, bias):
" 重み付き線形和の関数。"
return 0.0
def sigmoid(x):
" シグモイド関数。"
return 0.0
def identity(x):
" 恒等関数。"
return 0.0
w = [0.0, 0.0] # 重み(仮の値)
b = 0.0 # バイアス(仮の値)
next_x = x # 訓練データをノードへの入力に使う
# ---ここまでは仮の実装。ここからが必要な実装---
# 1つのノードの処理(1): 重み付き線形和
node_sum = summation(next_x, w, b)
# 1つのノードの処理(2): 活性化関数
is_hidden_layer = True
if is_hidden_layer:
# 隠れ層(シグモイド関数)
node_out = sigmoid(node_sum)
else:
# 出力層(恒等関数)
node_out = identity(node_sum)
1つのノードの順伝播処理に必要なことは、リスト3の通り、
- (1)重み付き線形和の関数: summation()関数として実装
- (2)活性化関数: ここではsigmoid()関数やidentity()関数として実装
という2つの数学関数だけです(図4)。
それぞれの関数の中身の実装を示します。
重み付き線形和
重み付き線形和(weighted linear summation、以下では「線形和」と表記)とは、あるノードへの複数の入力(x1、x2など)に、それぞれの重み(w1、w2など)を掛けて足し合わせて、最後にバイアス(b)を足した値です(前掲の図4の左。PyTorchのLinearクラスや、TensorFlow/KerasのDenseクラス、他にはAffine層などに相当します)。これをforループで記述したのがリスト4です。
def summation(x, weights, bias):
# ※1データ分、つまりxとweightsは「一次元リスト」という前提。
linear_sum = 0.0
for x_i, w_i in zip(x, weights):
linear_sum += x_i * w_i # iは「番号」(数学は基本的に1スタート)
linear_sum += bias
return linear_sum
# 線形代数を使う場合のコード例:
# linear_sum = np.dot(x, weights) + bias
ついでに、次回の逆伝播(の中で使う偏微分)で必要となる線形和の偏導関数(partial derivative function、本連載のコードでは全て「der」と記述する)をリスト5に実装しておきます。
def sum_der(x, weights, bias, with_respect_to='w'):
# ※1データ分、つまりxとweightsは「一次元リスト」という前提。
if with_respect_to == 'w':
return x # 線形和uを各重みw_iで偏微分するとx_iになる(iはノード番号)
elif with_respect_to == 'b':
return 1.0 # 線形和uをバイアスbで偏微分すると1になる
elif with_respect_to == 'x':
return weights # 線形和uを各入力x_iで偏微分するとw_iになる
引数with_respect_toについては、例えば「変数xに関しての関数f(x,w,b)の偏導関数」(=関数f(x,w,b)を変数xで偏微分すること)を、英語で「partial derivative of f(x,w,b) with respect to x」と表現するため、このように命名した。
線形和の式を各重み/バイアス/入力で偏微分すると、このような計算結果になります。繰り返しになりますが、数学計算の説明は割愛します。
※注意点として、引数として渡される入力xや重みweightsには、一次元リストの形で、前の層内に存在するノード数分の値が入っています(例えば図4の中央に示した「1つのノード」であれば、前の層のノード数が2個なので、2個の値が入ったリストになっています)。リスト5の偏微分では、例えばx1とx2という2つの変数に関してそれぞれで線形和の偏微分を行うことになるので、出力も2個の値が入ったリストになります。バイアスbは1つしかないので、float値になっています。
活性化関数:シグモイド関数
隠れ層では、最も基礎的なシグモイド関数(Sigmoid function)を固定的に使うことにします。シグモイド関数の説明と、それを実装したPython関数、その導関数は用語辞典を参考にしてください。リスト6にシグモイド関数、リスト7にその導関数の実装コードを掲載します。入力される値と出力される値はfloat値です。
import math
def sigmoid(x):
return 1.0 / (1.0 + math.exp(-x))
# 線形代数の場合はmathをnpに変える(事前にimport numpy as np)
def sigmoid_der(x):
output = sigmoid(x)
return output * (1.0 - output)
活性化関数:恒等関数
出力層では、回帰問題をイメージして、そのままの値を出力する活性化関数である恒等関数(Identity function)を使用します。こちらの用語辞典をご参考に。リスト8に恒等関数、リスト9にその導関数の実装コードを掲載します。
def identity(x):
return x
def identity_der(x):
return 1.0
以上で、リスト3で空で定義していた3つの関数の実装は終わりました。「1つのノードにおける処理」の実装もこれで完了です。
順伝播の処理全体の実装
ニューラルネットには、層があり、その中に複数のノードが存在するという構造です。従って、
- 各層を1つずつ処理するforループと
- 層の中のノードを1つずつ処理するforループの2段階構造が必要で
- その中に「1つのノードにおける処理」を記述
- 層の中のノードを1つずつ処理するforループの2段階構造が必要で
すればよいわけです。
その考えに沿って、順伝播の処理全体を行うforward_prop()関数を実装してみたのがリスト10です。補足説明のためのコメントも多めに含めているので少し長く見えると思いますが、ポイントとなる順伝播の本質部分は短いです。2つのforループと、「ノードごとの重みとバイアスを取得」している部分、【リスト3のコード】と記載された部分(特に太字で示した9行)に注目してください。それら以外のコードは、計算結果をキャッシュに保存(=記録)するためのこまごました処理なので、読み飛ばしても構いません。
※注意点として、リスト2で作成したmodel(=(layers, weights, biases)のタプル)とxを実引数として受け取れるよう、仮引数にlayers, weights, biasesとxを先頭に追加して、リスト1で作成したforward_prop()関数のシグネチャー(=関数の引数と、その組み合わせ)を改変しました。最後の方に「予測の実行例」として書いたforward_prop()関数の呼び出しでは、タプルであるmodelはイテラブル(=繰り返し可能なオブジェクト)なので、*イテラブルアンパック演算子を使って*modelと書くことで、先頭にある3つの仮引数に対してタプルごとまとめてセットしています(参考:「Python 3.5の新機能」)。
def forward_prop(layers, weights, biases, x, cache_mode=False):
"""
順伝播を行う関数。
- 引数:
(layers, weights, biases): モデルを指定する。
x: 入力データを指定する。
cache_mode: 予測時はFalse、訓練時はTrueにする。これにより戻り値が変わる。
- 戻り値:
cache_modeがFalse時は予測値のみを返す。True時は、予測値だけでなく、
キャッシュに記録済みの線形和(Σ)値と、活性化関数の出力値も返す。
"""
cached_sums = [] # 記録した全ノードの線形和(Σ)の値
cached_outs = [] # 記録した全ノードの活性化関数の出力値
# まずは、入力層を順伝播する
cached_outs.append(x) # 何も処理せずに出力値を記録
next_x = x # 現在の層の出力(x)=次の層への入力(next_x)
# 次に、隠れ層や出力層を順伝播する
SKIP_INPUT_LAYER = 1
for layer_i, layer in enumerate(layers): # 各層を処理
if layer_i == 0:
continue # 入力層は上で処理済み
# 各層のノードごとに処理を行う
sums = []
outs = []
for node_i in range(layer): # 層の中の各ノードを処理
# ノードごとの重みとバイアスを取得
w = weights[layer_i - SKIP_INPUT_LAYER][node_i]
b = biases[layer_i - SKIP_INPUT_LAYER][node_i]
# 【リスト3のコード】ここから↓
# 1つのノードの処理(1): 重み付き線形和
node_sum = summation(next_x, w, b)
# 1つのノードの処理(2): 活性化関数
if layer_i < len(layers)-1: # -1は出力層以外の意味
# 隠れ層(シグモイド関数)
node_out = sigmoid(node_sum)
else:
# 出力層(恒等関数)
node_out = identity(node_sum)
# 【リスト3のコード】ここまで↑
# 各ノードの線形和と(活性化関数の)出力をリストにまとめていく
sums.append(node_sum)
outs.append(node_out)
# 各層内の全ノードの線形和と出力を記録
cached_sums.append(sums)
cached_outs.append(outs)
next_x = outs # 現在の層の出力(outs)=次の層への入力(next_x)
if cache_mode:
return (cached_outs[-1], cached_outs, cached_sums)
return cached_outs[-1]
# 訓練時の(1)順伝播の実行例
y_pred, cached_outs, cached_sums = forward_prop(*model, x, cache_mode=True)
# ※先ほど作成したモデルと訓練データを引数で受け取るよう改変した
print(f'cached_outs={cached_outs}')
print(f'cached_sums={cached_sums}')
# 出力例:
# cached_outs=[[0.05, 0.1], [0.5, 0.5, 0.5], [0.0]] # 入力層/隠れ層1/出力層
# cached_sums=[[0.0, 0.0, 0.0], [0.0]] # 隠れ層1/出力層(※入力層はない)
コード中にもコメントを入れていますが、気を付けてほしいポイントを以下でも触れておきます。
まず、入力層は出力のみで、線形和や活性化関数がありません。よって、出力のキャッシュ(cached_outs)にだけ値を追加しています。その結果、線形和のキャッシュ(cached_sums)は入力層の1行分が少ないリスト内容になっていますので、利用する際に注意してください。
次に、各ノードの出力(xやouts)は、次の層にあるノードへの入力(next_x)に変化することを意識するのが大切です(コードのロジックを追う上で筆者自身が混乱しやすいと感じた部分です)。リスト10ではnext_x = ・・・・・・というコードで、その変化を明示的にしました。ここが層から層へデータが伝播していっているところに相当しますね。
ちなみにノートブックの方では、コード中にprint()関数を仕込むことで(※全てコメントアウトしています)、途中の計算内容が順番にテキスト出力されるようにしてみました。リスト10では、以下のように出力されます。
■第1層(入力層)-全て(2個)の特徴量:
●入力データ: 何もしない=out([0.05, 0.1])
■第2層-第1ノード:
●重み付き線形和: x_i(0.05)×w_i(0.0)+x_i(0.1)×w_i(0.0)+b(0.0)=sum(0.0)
●活性化関数(隠れ層はシグモイド関数): sigmoid(0.0)=out(0.5)
■第2層-第2ノード:
●重み付き線形和: x_i(0.05)×w_i(0.0)+x_i(0.1)×w_i(0.0)+b(0.0)=sum(0.0)
●活性化関数(隠れ層はシグモイド関数): sigmoid(0.0)=out(0.5)
■第2層-第3ノード:
●重み付き線形和: x_i(0.05)×w_i(0.0)+x_i(0.1)×w_i(0.0)+b(0.0)=sum(0.0)
●活性化関数(隠れ層はシグモイド関数): sigmoid(0.0)=out(0.5)
■第3層-第1ノード:
●重み付き線形和: x_i(0.5)×w_i(0.0)+x_i(0.5)×w_i(0.0)+
x_i(0.5)×w_i(0.0)+b(0.0)=sum(0.0)
●活性化関数(出力層は恒等関数): identity(0.0)=out(0.0)
cached_outs=[[0.05, 0.1], [0.5, 0.5, 0.5], [0.0]]
cached_sums=[[0.0, 0.0, 0.0], [0.0]]
数値が0.0ばかりなので参考になりませんね・・・・・・。後述のリスト11を参考に重みやバイアスなどを変えてみて、本当に計算通りになるかのチェックなどをしてみてもよいでしょう(※ノートブックの方には別の計算パターンのコードも入れておきました)。
順伝播による予測の実行例
ちなみに、予測時は途中の計算結果は不要なので、引数cache_modeを指定する必要がありません(リスト11)。
# 異なるDNNアーキテクチャーを定義してみる
layers2 = [
2, # 入力層の入力(特徴量)の数
3, # 隠れ層1のノード(ニューロン)の数
2, # 隠れ層2のノード(ニューロン)の数
1] # 出力層のノードの数
# 重みとバイアスの初期値
weights2 = [
[[-0.2, 0.4], [-0.4, -0.5], [-0.4, -0.5]], # 入力層→隠れ層1
[[-0.2, 0.4, 0.9], [-0.4, -0.5, -0.2]], # 隠れ層1→隠れ層2
[[-0.5, 1.0]] # 隠れ層2→出力層
]
biases2 = [
[0.1, -0.1, 0.1], # 隠れ層1
[0.2, -0.2], # 隠れ層2
[0.3] # 出力層
]
# モデルを定義
model2 = (layers2, weights2, biases2)
# 仮の訓練データ(1件分)を準備
x2 = [2.3, 1.5] # x_1とx_2の2つの特徴量
# 予測時の(1)順伝播の実行例
y_pred = forward_prop(*model2, x2)
print(y_pred) # 予測値
# 出力例:
# [0.3828840428423274]
非常にシンプルで原始的な実装ですが、このように任意の層数とノード数の全結合のDNN(Deep Neural Network)のアーキテクチャーを定義して、DNNモデルによる予測が行えます。
難点としては、前述の通り、重みを扱うエッジ(リンク)を自動生成していないため、手動で記述する必要があり、これがとても面倒なことです。エッジを層ごと、ノードごとに数え上げる必要がありますが、筆者の場合は「ニューラルネットワーク Playground - Deep Insider」で線を数えてから上のように定義しました(ご参考まで)。
今後のステップの準備:関数への仮引数の追加
以上で今回の内容は終わりなのですが、次回の内容を軽くするため、もう一つだけコードを書いておきます。
先ほどのリスト10でforward_prop()関数にlayers, weights, biasesという仮引数を追加して、実引数として*modelオブジェクトをセットできるようにしました。
同様に、リスト1で作成したback_prop()関数とupdate_params()関数にも同じ仮引数を追加して、関数のシグネチャーを改変しておきます(リスト12)。
def back_prop(layers, weights, biases, y_true, cached_outs, cached_sums):
" 逆伝播を行う関数。"
return None, None
def update_params(layers, weights, biases, grads_w, grads_b, lr=0.1):
" パラメーター(重みとバイアス)を更新する関数。"
return None, None
今回は逆伝播に入るための準備編、ウォームアップ回と呼べるものでした。「ここまでなら分かってたよ」という人も少なくないと思います。
また今回は「偏微分」という用語が出てきて、sum_der()/sigmoid_der()/identity_der()という3つの偏導関数を定義しました。これらは、次回の逆伝播の実装の中で呼び出します。
微分や偏微分について簡単に説明しておくと、微分とは「関数f(x)が描く曲線における、変数x地点での傾き」を求めることです。偏微分とは、関数がf(x,w,b)と多変数であるときの、変数x/変数w/変数bに関する微分です。偏微分の計算結果である偏微分係数が、ニューラルネットワークの重みやバイアスの「勾配(gradient)」となります。この勾配を使って重みやバイアスを更新することで、モデルを最適化していきます。
微分と導関数は高校数学、偏微分と偏導関数は大学数学の領域ですが、いずれも数学計算自体はそれほど難しくありません。「もっと知りたい」「自分で計算して、sum_der()/sigmoid_der()/identity_der()関数を何も見ずに実装したい」という人は、まずは微分なら「連載『AI・機械学習の数学入門 』の微分の回」から、偏微分なら「同連載の偏微分の回」から学び始めることをお勧めします。
さて次回は、いよいよ本題の逆伝播を説明します。お楽しみに。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

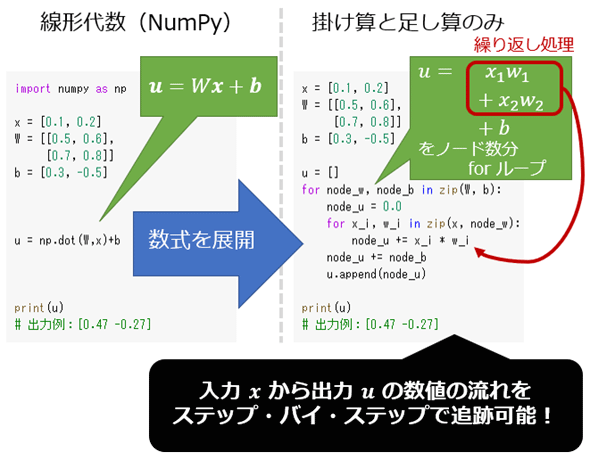


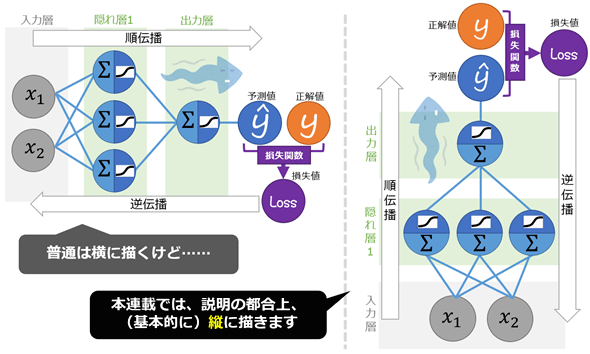
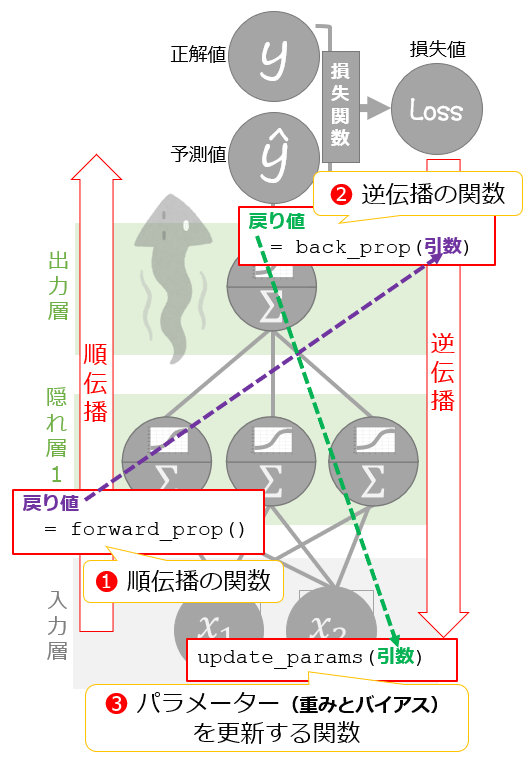 図3 訓練(学習)処理を示したニューラルネットワーク図
図3 訓練(学習)処理を示したニューラルネットワーク図