Pythonで実装するニューラルネットワークを完成させよう:ニューラルネットワーク入門
ニューラルネットワークをNumPy(線形代数)なしのPythonでフルスクラッチ実装する連載(基礎編)の前/中/後編の後編。いよいよ完成。最適化の処理をPythonコードから理解しよう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本稿は、ニューラルネットワーク(以下、ニューラルネット)の仕組みや挙動を、数学理論からではなくPythonコードから学ぶことを目標とした連載(基礎編)の最後となる第3回です。
前々回の第1回では、「ニューラルネットの訓練(学習)処理を実現するために必要なこと」として、
- ステップ(1)順伝播: forward_prop()関数として実装(前々回)
- ステップ(2)逆伝播: back_prop()関数として実装(前回)
- ステップ(3)パラメーター(重みとバイアス)の更新: update_params()関数として実装(今回)。これによりモデルが最適化される
という3大ステップを示しました。前回の第2回で、このうちの「ステップ(2)逆伝播」までの実装が完了しています。
今回はその続きとして、「ステップ(3)パラメーターの更新と、モデルの最適化」までを実装して、ニューラルネットの実装を完了させます。最後に、それを使って簡単な回帰問題を解いてみます。
ここからの内容は簡単です。その分、作業的なコーディング部分が多くなってしまいますが、最後の完成に至るまでを楽しんでコーディングしていきましょう。
※なお本稿は、第1回〜第2回とセットの内容なので、図や掲載コード(「リスト<数字>」と表記)などの番号は前回からの継続となっています。
ステップ3. パラメーター(重みとバイアス)更新の実装
それでは、今回も何も見ずにゼロからスクラッチでコードを書くという想定で進めていきます。
実装を始める前に、まずはもう一度、訓練(学習、最適化)処理全体の実装から振り返っておきましょう(前々回のリスト1)。
# 訓練処理
y_pred, cached_outs, cached_sums = forward_prop(cache_mode=True) # (1)
grads_w, grads_b = back_prop(y_true, cached_outs, cached_sums) # (2)
weights, biases = update_params(grads_w, grads_b, LEARNING_RATE) # (3)
前回は、back_prop()関数から戻り値としてgrads_w, grads_bという2つの勾配(gradients)情報を取得できるようにしました。今回はその勾配情報を使って、パラメーター(重みとバイアス)を更新していきます。
パラメーターを更新する目的は、もちろん分かっていると思いますが、ニューラルネットのモデルを最適化することです。以下に、最適化の考え方を簡単にまとめておきます。
※なお、本稿で説明するのは最も基礎的な勾配降下法(Gradient Descent)です。後述するSGD(確率的勾配降下法)もその一種で、他にはRMSpropやAdamなどより応用的な手法があります。SGD以外の場合は、重みパラメーターの更新方法も少し変わってきます。
図14は、教材などでよく見る「最適化の参考イメージ」で、1つの重みパラメーターしかない場合の損失関数のグラフです。このようなイメージで、重みパラメーターの数値を調整(=更新)しながら、坂の一番下まで進めていきます(※ちなみに、この図は2次元のグラフですが、2つの重みパラメーターがある場合の、3次元のグラフも教材などでよく見ます。3次元の場合は、谷の底に着くまで進めるイメージになります)。
更新時に、どちらの方向に、どれくらい進むかを表す数値が、前回で計算済みの「勾配」となります。坂の下に進むには、現在の「各重み」から「その勾配」を引き算した新しい「各重み」に更新します(※例えば、勾配が−の数値の場合は、坂道は右下りになります。坂の下に進むには今の数値に+しなければなりません。今の数値から−の勾配値を引く(−する)と+になるので、坂道を右下に進めます。勾配が+の数値の場合は、坂道を左下に進めます)。
ただし1回の更新(イテレーション)で一気に進むと、曲線の中を左右に行ったり来たりしてなかなか収束しない可能性があります。そこで1回(=オンライン学習なら1件のデータ、ミニバッチ学習ならバッチサイズ分のデータ)で進む距離が適度になるように、「学習率」(learning rate、η:イータ)を「勾配」に掛け算することで、進む大きさをスケーリングして調整します。
1つのパラメーターの更新
1つの重みパラメーターの更新をPythonコードで書くと、リスト23のようになります。簡単ですね。バイアスの場合も、wをbに変えるだけの同じ式です。
# 取りあえず仮で、変数を定義して、コードが実行できるようにしておく
w_ij = 0.0 # 各重み
b_j = 0.0 # バイアス
grad_w_ij = 0.2 # 各重みの勾配
grad_b_j = 0.2 # バイアスの勾配
LEARNING_RATE = 0.1 # 学習率(lr)
lr = LEARNING_RATE
# ---ここまでは仮の実装。ここからが必要な実装---
w_ij = w_ij - lr * grad_w_ij # 重みパラメーターの更新
b_j = b_j - lr * grad_b_j # バイアスパラメーターの更新
このコードは図15の計算式を表現したものです。
以上が分かれば、パラメーター(重みとバイアス)を更新するPython関数は実装できます。
パラメーター更新の処理全体の実装
またまた順伝播の実装と同じ説明内容になりますが、ニューラルネットは、層があり、その中に複数のノードが存在するという構造ですので、
- 各層を1つずつ処理するforループと
- 層の中のノードを1つずつ処理するforループの2段階構造が必要で
- その中に「1つのパラメーターの更新」を記述
- 層の中のノードを1つずつ処理するforループの2段階構造が必要で
すればよいわけです。
この考えに沿って、パラメーター更新の処理全体を行うupdate_params()関数を実装してみたのがリスト24です。2つのforループと、既に説明済みの「パラメーター更新」の実装(特に太字で示した4行)に注目してください。それら以外のコードは、更新した新しい「重み」と「バイアス」を多次元リストにまとめるためのこまごました処理なので、読み飛ばしても構いません。
def update_params(layers, weights, biases, grads_w, grads_b, lr=0.1):
"""
パラメーター(重みとバイアス)を更新する関数。
- 引数:
(layers, weights, biases): モデルを指定する。
grads_w: 重みの勾配。
grads_b: バイアスの勾配。
lr: 学習率(learning rate)。最適化を進める量を調整する。
- 戻り値:
新しい重みとバイアスを返す。
"""
# ネットワーク全体で勾配を保持するためのリスト
new_weights = [] # 重み
new_biases = [] # バイアス
SKIP_INPUT_LAYER = 1
for layer_i, layer in enumerate(layers): # 各層を処理
if layer_i == 0:
continue # 入力層はスキップ
# 層ごとで勾配を保持するためのリスト
layer_w = []
layer_b = []
for node_i in range(layer): # 層の中の各ノードを処理
b = biases[layer_i - SKIP_INPUT_LAYER][node_i]
grad_b = grads_b[layer_i - SKIP_INPUT_LAYER][node_i]
b = b - lr * grad_b # バイアスパラメーターの更新
layer_b.append(b)
node_weights = weights[layer_i - SKIP_INPUT_LAYER][node_i]
node_w = []
for each_w_i, w in enumerate(node_weights):
grad_w = grads_w[layer_i - SKIP_INPUT_LAYER][node_i][each_w_i]
w = w - lr * grad_w # 重みパラメーターの更新
node_w.append(w)
layer_w.append(node_w)
new_weights.append(layer_w)
new_biases.append(layer_b)
return (new_weights, new_biases)
注意点は特にありません。コード中のコメントを参考にしてください。
以上でupdate_params()関数が完成したので、試しに実行してみましょう。
パラメーター更新の実行例
リスト25のようなコードを書けば、順伝播から逆伝播、パラメーター更新までを続けて実行できます。
layers = [2, 2, 2]
weights = [
[[0.15, 0.2], [0.25, 0.3]],
[[0.4, 0.45], [0.5,0.55]]
]
biases = [[0.35, 0.35], [0.6, 0.6]]
model = (layers, weights, biases)
# 元の重み
print(f'old-weights={weights}')
print(f'old-biases={biases}' )
# old-weights=[[[0.15, 0.2], [0.25, 0.3]], [[0.4, 0.45], [0.5, 0.55]]]
# old-biases=[[0.35, 0.35], [0.6, 0.6]]
# (1)順伝播の実行例
x = [0.05, 0.1]
y_pred, cached_outs, cached_sums = forward_prop(*model, x, cache_mode=True)
# (2)逆伝播の実行例
y_true = [0.01, 0.99]
grads_w, grads_b = back_prop(*model, y_true, cached_outs, cached_sums)
print(f'grads_w={grads_w}')
print(f'grads_b={grads_b}')
# grads_w=[[[0.006706025259285303, 0.013412050518570607], [0.007487461943833829, 0.014974923887667657]], [[0.6501681244277691, 0.6541291517796395], [0.13937181955411934, 0.1402209162240302]]]
# grads_b=[[0.13412050518570606, 0.14974923887667657], [1.09590596705977, 0.23492140409646534]]
# (3)パラメーター更新の実行例
LEARNING_RATE = 0.1 # 学習率(lr)
weights, biases = update_params(*model, grads_w, grads_b, lr=LEARNING_RATE)
# 更新後の新しい重み
print(f'new-weights={weights}')
print(f'new-biases={biases}')
# new-weights=[[[0.14932939747407145, 0.19865879494814295], [0.2492512538056166, 0.2985025076112332]], [[0.3349831875572231, 0.3845870848220361], [0.48606281804458806, 0.5359779083775971]]]
# new-biases=[[0.3365879494814294, 0.33502507611233234], [0.490409403294023, 0.5765078595903534]]
# モデルの最適化
model = (layers, weights, biases)
以上で、「ステップ(1)順伝播」「ステップ(2)逆伝播」「ステップ(3)パラメーター(重みとバイアス)の更新」を担う3つの関数の実装が完了しました。あとは、これら3つの関数を呼び出す最適化処理を実装して完成です。
3つのステップを呼び出す最適化処理の実装
最適化処理:学習方法と勾配降下法
最適化処理を行う代表的な学習方法には幾つかの種類があります(参考:「ディープラーニング最速入門」)。実装を始める前に、代表的な学習方法を簡単にまとめておきます。
- オンライン学習(Online training): データ1件ずつ訓練していくこと
- ミニバッチ学習(Mini-batch training): 小さなまとまりのデータごとに訓練していくこと
- バッチ学習(Batch training): データ全件で訓練していくこと
このうち、オンライン学習やミニバッチ学習では、データをランダムにシャッフルすること(=統計学の確率論におけるランダムサンプリング、無作為抽出をすること)で、(標本/サンプルである)訓練ごとのデータの分布が、(母集団である)データ全体の縮図になるようにします(※なお、バッチ学習のデータをシャッフルしても、データ全件を使うので無意味です。訓練時ではなく評価時は、再現性を保つためにもシャッフルしないのが一般的です)。このため、オンライン学習やミニバッチ学習の勾配降下法は、「確率的」勾配降下法(SGD)と呼ばれます。
学習方法ごとに、勾配降下法をまとめると以下のようになります。
- SGD(Stochastic Gradient Descent): オンライン学習
- ミニバッチSGD(Mini-batch SGD): ミニバッチ学習。単にミニバッチ勾配降下法(Mini-batch Gradient Descent)とも呼ぶ
- 最急降下法(Steepest Descent): バッチ学習。バッチ勾配降下法(Batch Gradient Descent)とも呼ぶ
最適化の実装は、バッチサイズでデータを処理しない分、オンライン学習のSGDが一番簡単で、説明する上でも分かりやすい内容になると思います。しかし今回は、コード内容も簡単なので少し難易度を上げて、あえて全ての学習方法に対応できる実装コードにしてみます。
最適化の処理全体の実装
訓練処理では、エポック(=全データ分で1回の訓練)があり、その中にイテレーション(=バッチサイズごとでのパラメーターの更新)が存在するという構造ですので、
- エポックを1回ずつ処理するforループと
- その中にデータを1件ずつ処理するforループの2段階構造を用意し
- その中に「ステップ(1)順伝播」「ステップ(2)逆伝播」と
- イテレーションごとに「ステップ(3)パラメーターの更新」を記述
- その中にデータを1件ずつ処理するforループの2段階構造を用意し
するようにします(※あくまで筆者による実装方針の例です)。
この考えに沿って訓練(最適化)処理を実装しますが、階層が深くなる上にコードの行数が少し長いので、説明の都合上、上の箇条書きの前半2行をリスト26(train()親関数)、後半2行をリスト27(optimize()子関数)、という親子関係の2つの関数に分けて記述します。※1つの関数として実装した方がシンプルになって見通しもよくなるので、本来であればそうした方がよいと思います。
まずリスト26の訓練処理では、2つのforループと、「訓練データのインデックスをランダムにシャッフル」している部分、リスト27で実装するoptimize()関数を呼び出して戻り値として返された損失値(loss)を蓄積(accumulate)している部分(acm_loss変数)(特に太字で示した7行)に注目してください。※シャッフルはデータ内容自体ではなく、データのインデックスだけをシャッフルしています。
import random
# 取りあえず仮で、空の関数を定義して、コードが実行できるようにしておく
def optimize(model, x, y, data_i, last_i, batch_i, batch_size, acm_g, lr=0.1):
" モデルを最適化する関数(子関数)。"
loss = 0.1
return model, loss, batch_i, acm_g
# ---ここまでは仮の実装。ここからが必要な実装---
def train(model, x, y, batch_size=32, epochs=10, lr=0.1, verbose=10):
"""
モデルの訓練を行う関数(親関数)。
- 引数:
model: モデルをタプル「(layers, weights, biases)」で指定する。
x: 訓練データ(各データが行、各特徴量が列の、2次元リスト値)。
y: 訓練ラベル(各データが行、各正解値が列の、2次元リスト値)。
batch_size: バッチサイズ。何件のデータをまとめて処理するか。
epochs: エポック数。全データ分で何回、訓練するか。
lr: 学習率(learning rate)。最適化を進める量を調整する。
verbose: 訓練状況を何エポックおきに出力するか。
- 戻り値:
損失値の履歴を返す。これを使って損失値の推移グラフが描ける。
"""
loss_history = [] # 損失値の履歴
data_size = len(y) # 訓練データ数
data_indexes = range(data_size) # 訓練データのインデックス
# 各エポックを処理
for epoch_i in range(1, epochs + 1): # 経過表示用に1スタート
acm_loss = 0 # 損失値を蓄積(accumulate)していく
# 訓練データのインデックスをシャッフル(ランダムサンプリング)
random_indexes = random.sample(data_indexes, data_size)
last_i = random_indexes[-1] # 最後の訓練データのインデックス
# 親関数で管理すべき変数
acm_g = (None, None) # 重み/バイアスの勾配を蓄積していくため
batch_i = 0 # バッチ番号をインクリメントしていくため
# 訓練データを1件1件処理していく
for data_i in random_indexes:
# 親子に分割したうちの子関数を呼び出す
model, loss, batch_i, acm_g = optimize(
model, x, y, data_i, last_i, batch_i, batch_size, acm_g, lr)
acm_loss += loss # 損失値を蓄積
# エポックごとに損失値を計算。今回の実装では「平均」する
layers = model[0] # レイヤー構造
out_count = layers[-1] # 出力層のノード数
# 「訓練データ数(イテレーション数×バッチサイズ)×出力ノード数」で平均
epoch_loss = acm_loss / (data_size * out_count)
# 訓練状況を出力
if verbose != 0 and \
(epoch_i % verbose == 0 or epoch_i == 1 or epoch_i == EPOCHS):
print(f'[Epoch {epoch_i}/{EPOCHS}] train_loss: {epoch_loss}')
loss_history.append(epoch_loss) # 損失値の履歴として保存
return model, loss_history
# サンプル実行用の仮のモデルとデータ
layers = [2, 2, 2]
weights = [
[[0.15, 0.2], [0.25, 0.3]],
[[0.4, 0.45], [0.5,0.55]]
]
biases = [[0.35, 0.35], [0.6, 0.6]]
model = (layers, weights, biases)
x = [[0.05, 0.1]]
y = [[0.01, 0.99]]
# モデルを訓練する
BATCH_SIZE = 2 # バッチサイズ
EPOCHS = 1 # エポック数
LEARNING_RATE = 0.02 # 学習率(lr)
model, loss_history = train(model, x, y, BATCH_SIZE, EPOCHS, LEARNING_RATE)
# 出力例:
# [Epoch 1/1] train_loss: 0.05
コード中にもコメントを入れていますが、気を付けてほしいポイントを以下でも触れておきます。
リスト26では、各データごとに蓄積した損失値(=各エポック内の損失値の合計)をデータ数(data_size、出力ノード数のout_countは後述)で割って平均しています(厳密には、イテレーション、つまりバッチサイズごとの平均損失値を計算した後で、エポックごとに平均損失値を計算する方がよいです)。
前回の実装では、損失関数に二乗和誤差(SSE:Sum of Squared Error)を採用しました。よって、合計の1/2(1/2 × Σ)という損失値を計算すべきです(1/2の部分は、損失関数やその偏導関数の実装の中で計算済みです)。しかし、リスト26でデータ数(上記の通り、厳密にはバッチサイズ)で平均している段階で、実質的には「1/2した平均二乗誤差(MSE:Mean Squared Error)」を使っていることに相当します(平均の1/2で1/2n × Σになっているので、完全なMSEでもないです)。
このように損失関数を和(合計)から平均に変更したので、各勾配もバッチサイズごとに蓄積(後掲のリスト27のacm_gw変数やacm_gb変数)した後で、それをバッチサイズ(現在のバッチ数を意味するbatch_i)で割って平均する必要があります。
なお、この「平均」の部分は、単に合計(Σ)や、合計の1/2(1/2 × Σ)、平均(1/n × Σ)、平均の1/2(1/2n × Σ)、その他の正規化など、のいずれのスケール調整(スケーリング)を行っても、最終的には学習率によってスケール調整されることになるので、結果は基本的に変わりません。しかし合計だけの場合、バッチサイズを変更するたびに学習率でスケールを調整しなければならなくなります。平均ならスケールは変わらないので調整しなくてよいです。そのため本稿では「平均」することにしました。
実際にどうするかは、基本的に実装の目的や損失関数の計算式に依存します。分類問題では、交差エントロピー誤差などの損失関数に従い、基本的に平均します。また回帰問題では、平均二乗誤差などの損失関数に従い、基本的に平均します。
※ここからは細かい話になりますが、損失関数やその偏微分係数(勾配)を合計するか平均するかについて、もう一点だけ考慮しておくべきことがあります。それが回帰問題の場合に、モデルからの出力(=出力層のノード数)が2個以上あるケースです。
ちなみに分類問題の場合は、モデルからの出力数は、基本的に分類のクラス数に対応しており、全クラスを足して1つの問題に対する1つの解答となります。交差エントロピー誤差もそういう定義となっていますので、ここで考慮すべき点はないと思います。
回帰問題を解くモデルにおいて、1つのモデルから2個以上の出力があること(Multi-output regression)は一般的にあまりないケースではないかと思います。筆者が考えたケースとしては、例えば賃貸住宅価格と賃貸駐車場価格の両方を同時に出力する1つのモデルです(他には例えばX/Y/Z座標の3つを出力するモデルなど)。これは、2つの問題に対する2つの解答を同時に出力する1つのモデルとなっています。
この場合、2つの出力値は問題/目的が違う独立した値ですので、それぞれに対して損失値を計算することになりますが、1つのモデルを損失値で評価するためには1つの損失値にまとめる必要があります。まとめる際に、2つの独立した損失値を合計するか平均するかは、SSEではデータ数を「合計」するので出力ノード数分も「合計」するのが基本で、MSEではデータ数で「平均」するので出力ノード数分でも「平均」するのが基本になると筆者は考えています。
ライブラリーでの実装を一つの参考とするなら、PyTorchのMSELossの計算を筆者が試して確認したところ、「バッチサイズが5個」で「出力ノード数が10個」の回帰モデルで、MSELossをreduction='mean'(平均)にした場合は、5×10の50個(=バッチサイズ×出力ノード数)で割られた損失値が得られました。reduction='sum'(合計)にした場合は、単に合計された損失値が得られました。勾配でも同様です(参考:「Loss reduction sum vs mean: when to use each? - PyTorch Forums」)。
ちなみに、前述の通り通常は「平均」を使った方がよいわけですが、あえて「合計」を使う目的としては、平均や正規化などの処理を実装者が自由にカスタマイズしたいときだと思います。
今回の最適化の実装では、PyTorchの「平均」の実装に合わせて、損失関数やその偏微分係数(勾配)は「データ数(バッチサイズ)」と「出力層のノード数(out_count)」の両方で平均することとします。
さて、少し脱線しましたが、話を元に戻します。リスト26には特に難しいところはないと思います。
次のリスト27では、「ステップ(1)順伝播」「ステップ(2)逆伝播」「ステップ(3)パラメーター(重みとバイアス)の更新」を担う3つの関数を呼び出しています。また、重み勾配などの多次元リストの要素同士の足し算をaccumulate()関数として、要素ごとの平均をmean_element()関数として実装しました(※最適化の本質とは関係がないロジックなので、ここはカンニングOKです。Colabノートブックには、それぞれの関数でNumPyを利用するバージョンをコメントアウトした状態で含めておきました)。今回の実装例の難点として、訓練(最適化)処理の関数を2つに分けたため、蓄積する値や更新したモデルなどを戻り値で返すなどの手間が増えてしまっています。
def accumulate(list1, list2):
"2つのリストの値を足し算する関数。"
new_list = []
for item1, item2 in zip(list1, list2):
if isinstance(item1, list):
child_list = accumulate(item1, item2)
new_list.append(child_list)
else:
new_list.append(item1 + item2)
return new_list
def mean_element(list1, data_count):
"1つのリストの値をデータ数で平均する関数。"
new_list = []
for item1 in list1:
if isinstance(item1, list):
child_list = mean_element(item1, data_count)
new_list.append(child_list)
else:
new_list.append(item1 / data_count)
return new_list
def optimize(model, x, y, data_i, last_i, batch_i, batch_size, acm_g, lr=0.1):
"train()親関数から呼ばれる、最適化のための子関数。"
layers = model[0] # レイヤー構造
each_x = x[data_i] # 1件分の訓練データ
y_true = y[data_i] # 1件分の正解値
# ステップ(1)順伝播
y_pred, outs, sums = forward_prop(*model, each_x, cache_mode=True)
# ステップ(2)逆伝播
gw, gb = back_prop(*model, y_true, outs, sums)
# 各勾配を蓄積(accumulate)していく
if batch_i == 0:
acm_gw = gw
acm_gb = gb
else:
acm_gw = accumulate(acm_g[0], gw)
acm_gb = accumulate(acm_g[1], gb)
batch_i += 1 # バッチ番号をカウントアップ=現在のバッチ数
# 訓練状況を評価するために、損失値を取得
loss = 0.0
for output, target in zip(y_pred, y_true):
loss += sseloss(output, target)
# バッチサイズごとで後続の処理に進む
if batch_i % BATCH_SIZE != 0 and data_i != last_i:
return model, loss, batch_i, (acm_gw, acm_gb) # バッチ内のデータごと
layers = model[0] # レイヤー構造
out_count = layers[-1] # 出力層のノード数
# 平均二乗誤差なら平均する(損失関数によって異なる)
grads_w = mean_element(acm_gw, batch_i * out_count) # 「バッチサイズ ×
grads_b = mean_element(acm_gb, batch_i * out_count) # 出力ノード数」で平均
batch_i = 0 # バッチ番号を初期化して次のイテレーションに備える
# ステップ(3)パラメーター(重みとバイアス)の更新
weights, biases = update_params(*model, grads_w, grads_b, lr)
# モデルをアップデート(=最適化)
model = (layers, weights, biases)
return model, loss, batch_i, (acm_gw, acm_gb) # イテレーションごと
# サンプル実行
model, loss_history = train(model, x, y, BATCH_SIZE, EPOCHS, LEARNING_RATE)
# 出力例:
# [Epoch 1/1] train_loss: 0.31404948868496607
コード中にもコメントを入れていますが、気を付けてほしいポイントを以下でも触れておきます。
リスト27では、「リスト25 パラメーター更新の実行例」と同じように3つのステップを表現する関数を呼び出していますが、「ステップ(1)順伝播」や「ステップ(2)逆伝播」の関数は1件1件のデータごとに呼び出して、重みの勾配とバイアスの勾配を蓄積していっています(acm_gw変数とacm_gb変数)。蓄積数がバッチサイズに達した時、もしくはデータの最後に達した時に、「ステップ(3)パラメーター(重みとバイアス)の更新」の関数を呼び出しています。呼び出す前に、前述の通り、蓄積してきた各勾配を「バッチサイズ×出力層のノード数」で平均していますね。
以上で全て完成です。次に、何か回帰問題を解いてみましょう。
回帰問題を解くデモ
ニューラルネットをフルスクラッチ実装する内容の解説は終わっています。ここでは、デモを示すだけなので、コード内容の説明は割愛します。どういう回帰問題を、今回作成したニューラルネットの仕組みでどのように解けるかを確認してください。Colabノートブックで実行することが可能です。
今回使う回帰問題の訓練データは、「回帰問題をディープラーニング(基本のDNN)で解こう」でも使っているライブラリー「playground-data」の平面(Plain)データセットです。
特徴量(入力データ)はx1(X軸)とx2(Y軸)の座標です。その座標点における色、具体的にはオレンジ色(-1)〜灰色(0)〜青色(1)を予測する回帰問題となります。図16は訓練「前」のモデルによる予測状態を図示したものになります(※データセットはランダムに自動生成されるので実行のたびに変わります)。
それぞれの丸い点の座標は、訓練データ1件1件の特徴量を表します。その点の色が正解ラベルです。例えば左下の座標点でれば、色はオレンジ色、つまり-1.0に近い値が正解となります。右上が青色、つまり1.0に近い値が正解です。
モデルによる予測値は、背景色として描画されています。図16では全面が灰色です。これは、どの座標を入力しても、0.0が予測されることを意味します。これをニューラルネットで学習することで、オレンジ色の座標点の背景色はオレンジ色に、青色の座標点の背景色は青色に描画されるようにします。
ニューラルネットとその訓練処理の実装自体は簡単です。リスト28のように、まず訓練データを用意して、次にモデルを定義したら、最後に訓練処理のtrain()関数を呼び出すだけです。
# !pip install playground-data
import matplotlib.pyplot as plt
# 訓練データを取得
import plygdata as pg
PROBLEM_DATA_TYPE = pg.DatasetType.RegressPlane
TRAINING_DATA_RATIO = 0.5
DATA_NOISE = 0.0
data_list = pg.generate_data(PROBLEM_DATA_TYPE, DATA_NOISE)
X_train, y_train, _, _ = pg.split_data(data_list, training_size=TRAINING_DATA_RATIO)
# モデルを定義
layers = [2, 3, 1]
weights = [
[[0.0, 0.0], [0.0, 0.0], [0.0, 0.0]],
[[0.0, 0.0, 0.0]]
]
biases = [
[0.0, 0.0, 0.0], # hidden1
[0.0] # output
]
model = (layers, weights, biases)
# 訓練用のハイパーパラメーター設定
BATCH_SIZE = 4 # バッチサイズ
EPOCHS = 100 # エポック数
LERNING_RATE = 0.02 # 学習係数
# 訓練処理の実行
model, loss_history = train(model, X_train, y_train, BATCH_SIZE, EPOCHS, LEARNING_RATE)
# 学習結果(損失)のグラフを描画
epochs = len(loss_history)
plt.plot(range(1, epochs + 1), loss_history, marker='.', label='loss (Training data)')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
訓練結果として、エポック10件(train()関数の引数verboseで変更可能)ごとに損失値が出力されます。また、最後に損失値の履歴をグラフで表示しています(図17)。
グラフは理想的な形で収束していますね。訓練「後」のモデルによる予測状態を図示すると、図18のようになりました。
座標点の色と背景色が溶け合っており、ほぼ同じ色です。非常に高い精度のモデルですね。線形代数(NumPy)なしで作ってきた自作のニューラルネットで、確かに回帰問題を解けることが確認できました。お疲れさまでした。
いかがだったでしょうか。「線形代数を使ったコードでは理解できなかったけど、本連載(基礎編)なら理解できた」という人がいれば、筆者として本望です。そうでなくとも、本連載が何らかの理解の一助になっているのであれば、筆者としてうれしいです。
本連載(基礎編)を執筆するに当たって、さまざまな実装を試しました。そこでは、クラス定義でライブラリーっぽく使えるようにしたり、その中では線形代数を使ったり、さまざまな活性化関数や重みの初期化関数なども実装したりしました。本連載(基礎編)の続編として、そういったより詳細で発展的な内容を月に1本ぐらいのペースで公開していこうと考えています。
Copyright© Digital Advantage Corp. All Rights Reserved.



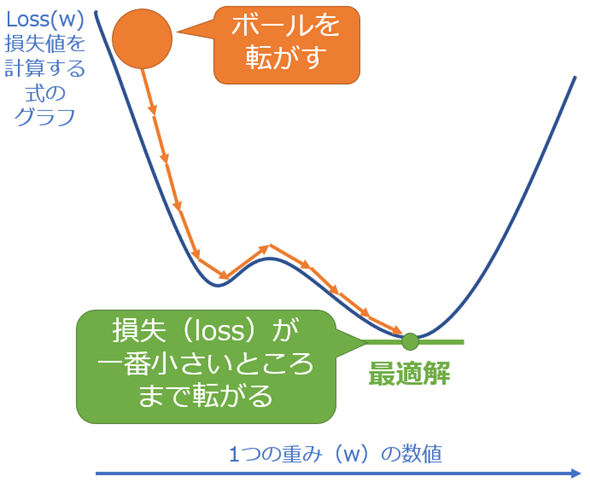
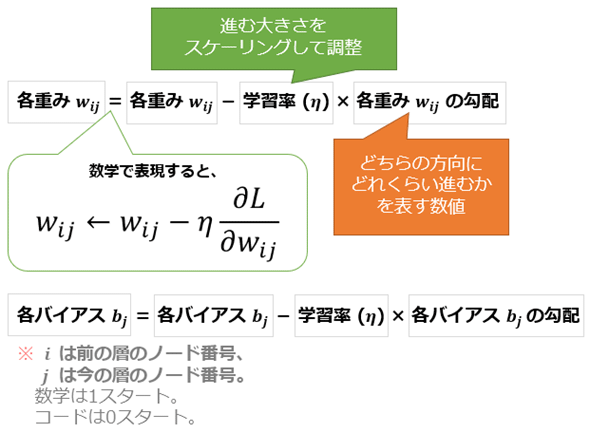
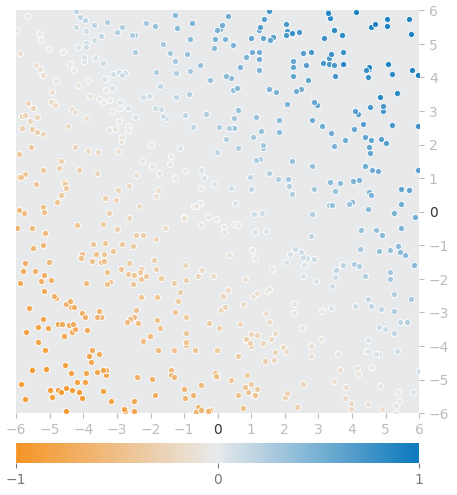 図16 訓練「前」のモデルによる予測状態
図16 訓練「前」のモデルによる予測状態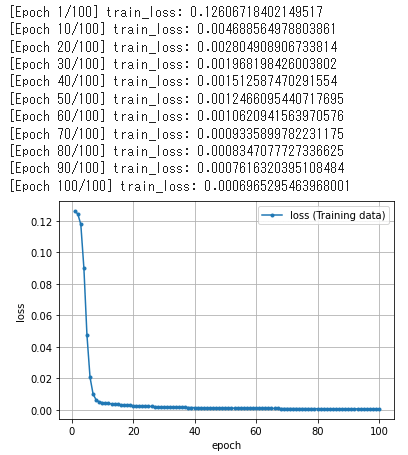 図17 回帰問題を解くデモの出力例
図17 回帰問題を解くデモの出力例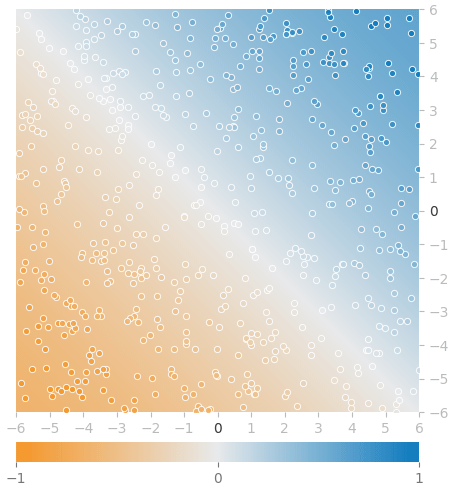 図18 訓練「後」のモデルによる予測状態
図18 訓練「後」のモデルによる予測状態



