残差平方和(RSS:Residual Sum of Squares)/[損失関数]二乗和誤差(SSE:Sum of Squared Error)とは?:AI・機械学習の用語辞典
用語「残差平方和」「二乗和誤差」について説明。残差平方和は、線形回帰の最小二乗法で用いられる関数の一つで、各データに対して「観測値と予測値の差(=残差)」の平方値を計算し、それを総和した値を表す。二乗和誤差は、損失関数の一つで、各データに対して「予測値と正解値の差(=誤差)」の二乗値を計算し、それを総和した値、もしくはさらにそれを2で割った値を表す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
統計学/機械学習における残差平方和(RSS:Residual Sum of Squares、二乗和残差)とは、各データに対して「観測値と予測値の差(=残差:residual)」の平方(=二乗)値を計算し、それを総和した値を出力する関数である。なお残差を、「観測値−予測値」ではなく「予測値−観測値」と計算しても結果は同じである。
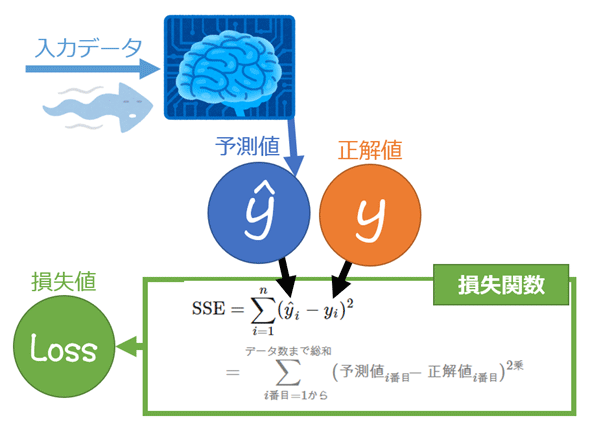
同様に、機械学習における二乗和誤差(SSE:Sum of Squared Error)とは、各データに対して「予測値と正解値の差(=誤差:error)」の二乗値を計算し、それを総和した値を出力する関数である(図1)。ただし、微分後の計算がよりシンプルになるように、先ほどの計算にさらに1/2を掛けることが一般的だ(※変数の二乗値を微分すると、変数の係数として2が出る。例えばx2を微分すると2xとなる。そこで、それに1/2を掛けてあげれば、xとシンプルになる)。なお誤差は、「予測値−正解値」ではなく「正解値−予測値」でもよい。
用途
残差平方和は、主に線形回帰において、最小二乗法でモデルのパラメーターを求める際に用いられる。また、決定係数R2という線形回帰用の評価関数の中でも、残差変動(=残差平方和)の式として用いられる。
一方、二乗和誤差は、残差平方和と数式がほぼ同じではあるが、主にニューラルネットワークの損失関数として用いられる。その式自体は、より一般的な損失関数である平均二乗誤差と酷似しているが、平均二乗誤差(MSE)が平均する、つまりデータ数で割る(=1/nを掛ける)のに対し、二乗和誤差(SSE)は平均しない、もしくは2で割る(=1/2を掛ける)という違いがある。ニューラルネットワークの初学者向けの教科書では、手計算が楽になるように、MSEではなく今回のSSEが用いられることがよくある。
なお、本稿では書き分けたが、残差平方和と二乗和誤差は同じものとして扱われることも多いので注意してほしい。また、二乗和誤差と平均二乗誤差が同じものとして扱われることもある。つまり、これらは用語名ではなく実際の計算式を見て「何をやっているか」を理解する方が無難である。
「残差平方和」の定義と数式
残差平方和(RSS)の数式は、次のようになる。統計学に寄せて「観測値(observed value)」と表記したが、「実測値」「実際の測定値」の他、さまざまな方法で収集したデータがこの対象となる。
「二乗和誤差」の定義と数式
二乗和誤差(SSE)の数式は、次のようになる。
前述の通り、1/2を掛ける(=2で割る)場合は、次のような式になる。
ちなみに、上記の残差平方和と二乗和誤差の数式では、「観測値(正解値)−予測値」と「予測値−正解値(観測値)」という計算の違いがあることに気付いたかもしれない。この計算は前述した通りにどちらにしてもよいが、このように書き分けたのは、筆者が以下のように考えているからである(人によって考え方が違うかもしれないので、一つの意見として参考程度に見ておいていただけるとうれしい)。
「残差」とは、全ての説明変数を考慮した後で残ったものを意味するため、それを素直に数式に表現すると「観測値−予測値」となる。例えば観測値(正解値)が2で予測値が1なら、2−1で、そのモデルによる予測では+1が残ってしまう(=そのモデルによって説明されていない部分)ということだ。そういう観点では、結果が同じになるとはいえ「予測値−観測値」という計算式にするのは先ほどの意味を表現できていないと思うので、あまりふさわしくないかもしれない。
一方の「(予測)誤差」とは、予測値が正解値からどれぐらいズレているかを意味するため、それを素直に数式に表現すると「予測値−正解値」となる。例えば予測値が1で正解値が2なら、1−2で、そのモデルによる予測値が正解値から−1分ズレているということになる。もちろん、同じ事象を「正解値(2)が予測値(1)から+1分ズレている」と表現することもできると思うので、そう考えるなら「正解値−予測値」という計算式でもよいだろう。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ