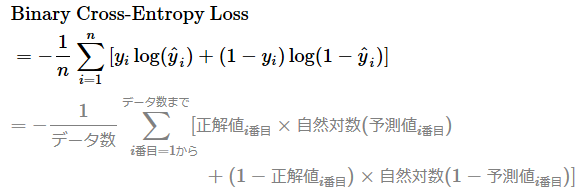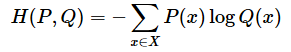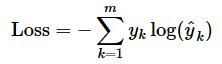［損失関数］交差エントロピー（Cross-Entropy）とは？：AI・機械学習の用語辞典

用語「交差エントロピー」について説明。分類タスクを解くための機械学習モデルの訓練に広く用いられる損失関数の一つで、「“正解ラベルの確率分布”から“モデル出力の確率分布”がどれくらいズレている（＝不一致）か」を数値で表す。特に、ロジスティック回帰やニューラルネットワークの分類タスクでよく使用される。

[一色政彦，デジタルアドバンテージ]

印刷

通知 連載「AI・機械学習の用語辞典」の新着をメールで通知

見るPost

Shareシェア

はてなブックマーク

SharePocket Button

連載目次

用語解説

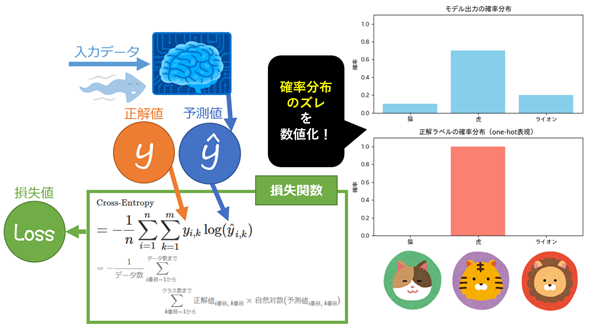
　情報理論／統計学／機械学習における交差エントロピー（Cross-entropy）とは、分類タスクにおいて、各データに対して「正解ラベルの確率分布」と「モデル出力によって得られる確率分布」のズレ（＝不一致）を自然対数を用いて数値化する関数である（図1）。

　得られた数値は損失（loss）や誤差（error）の値であるため、Cross-entropy loss（交差エントロピー損失）や交差エントロピー誤差（Cross-entropy error）とも呼ばれる。その損失値が小さいほどモデルの予測が正解に近く、大きいほど予測が外れていることを示す。

図1　「交差エントロピー」のイメージ

　そもそも分類タスクとは、例えば「犬か／どうか（例：猫か）」を判定するような2クラスの問題（＝二値分類）や、「猫／虎／ライオン」の中から1つを判定するような3クラス以上の問題（＝多クラス分類）を指す。このような問題を解くためのモデルの出力は、通常「確率分布」（厳密には、図1の右側に示すような棒グラフ状の分布で、二値分類なら「ベルヌーイ分布」、多クラス分類なら「カテゴリカル分布」）として解釈される。また、正解を示すラベル（例えば「猫」「虎」「ライオン」のどれが正解か）も、同様に「確率分布」として扱われる。

　そして、「“正解の確率分布（＝真の確率分布）”から“予測の確率分布”がどれだけズレているか」を数値化するのが交差エントロピーである。では、その「確率分布」とは具体的にどのようなものか、予測（モデル出力）と正解ラベルに分けて簡単に説明しておこう。

確率分布としてのモデル出力

　ロジスティック回帰やニューラルネットワークで二値分類タスクを解く場合、モデルは1つのクラスに属する確率（例えば「犬」の確率が何％か）を出力する。この確率は基本的にシグモイド関数（＝ロジスティック関数）によって計算され、確率値は0.0～1.0の範囲になる。具体例を挙げるなら、「犬である確率が0.8」のような出力となり（自動的に「残りのそれ以外（例：猫）である確率は0.2」となり）、1つのクラスに属する可能性を確率として示す。このため二値分類の場合、モデル出力は2つの棒からなる確率分布のグラフとして表現できる。

　一方、ソフトマックス回帰（＝多項ロジスティック回帰）やニューラルネットワークで多クラス分類タスクを解く場合、モデルは複数のクラス全てに対して、各クラスに属する確率を出力する。この確率は、基本的にソフトマックス関数によって計算され、各クラスの確率値の合計は1.0になる。具体例を挙げるなら、「猫：0.1、虎：0.7、ライオン：0.2」のような出力となり、どのクラスに属する可能性が高いかを確率として示す。このため多クラス分類の場合、モデル出力は複数の棒によって構成される確率分布のグラフとして表現できる（図1の右上）。

　このように「モデルの出力」は確率分布で表せるので、当然、正解ラベルも同じように確率分布として扱うことができる。

確率分布としての正解ラベル

　二値分類タスクでは、正解ラベル（＝真の値）は通常、0または1の値を取る。例えば、「犬なら1（＝100％）、それ以外（例：猫）なら0（＝0％）」というように、1つのクラス（ここでは犬）に属するかどうかを確率として示す。このため二値分類の場合、正解ラベルは2つの棒（＝この例では「犬の棒」＋「それ以外の棒」）からなる確率分布のグラフとして表現できる。

　一方、多クラス分類タスクでは、正解である1つのクラスだけに1を、その他の全てのクラスに0を割り当てたベクトル（例えば[0, 1, 0]）を使う。このようなベクトル表現を、one-hot表現（one-hot expression：ワン・ホット表現）と呼ぶ。

　元のラベルが「犬：1、虎：2、ライオン：3」といったカテゴリカル変数であっても、それを各クラスごとに0か1で表して「犬：[1, 0, 0]、虎：[0, 1, 0]、ライオン：[0, 0, 1]」のようなone-hot表現形式に変換できる。このような変換処理のことをone-hotエンコーディング（one-hot encoding）と呼ぶ。

　例えば、3クラス（猫／虎／ライオン）の分類で「虎」が正解であれば、正解ラベルは[0, 1, 0]となる。これは「虎クラスの確率が100％、他のクラス（猫／ライオン）の確率は全て0％」を意味し、正解ラベルは3つの棒（猫／虎／ライオン）によって構成される確率分布のグラフとして表現できる（図1の右下）。

　※なお、先ほどの二値分類の正解ラベル（0または1）も、「クラス0が正解なら[1, 0]、クラス1が正解なら[0, 1]」と見なせるため、one-hot表現の一種と解釈できる。

定義と数式

　冒頭では文章によって交差エントロピーの概要を説明したが、ここではより厳密に、数式でその定義を示す。二値分類と多クラス分類で数式の形が異なるため、それぞれに分けて説明する。

二値分類（Binary Classification）のクロスエントロピー損失

　ここでは、nはデータ数（iはその何番目か）、logは自然対数（＝ln、つまりネイピア数eを底とする対数）、Σは総和を表す。

　この関数の出力値は「損失」もしくは「誤差」を表し、冒頭でも説明した通り、その損失値が小さいほど予測精度が高いことを表す。

多クラス分類（Multi-class Classification）のクロスエントロピー損失

　ここでは、mはクラス数（kはその何番目か）を表す。それ以外の数学記号は先ほどと同じ意味である。正解ラベルのyはone-hot表現形式であることに注意してほしい。

LogLoss（対数損失）との関係

　以上で示した2種類の交差エントロピー損失の計算方法は、評価指標であるLogLoss（Logarithmic Loss）と基本的に同じだ。

KLダイバージェンスとの関係

　交差エントロピー損失と同様に、KLダイバージェンス（カルバック・ライブラー情報量）も「正解ラベルの確率分布P（KLダイバージェンスでは真の分布）」と「予測結果の確率分布Q（KLダイバージェンスでは近似分布）」の間のズレ（＝不一致）を測定するためのものだ。以下は、KLダイバージェンスの定義式である。

• D_KL …… 「KLダイバージェンス」（＝カルバック・ライブラー情報量）を指す。
• ‖ …… 「比較対象の区切り」を表す。例えば(P ‖ Q)は「Pを基準にQとの違いを測ること」を意味する。

　二値分類でも多クラス分類でも、特に正解ラベルをone-hot表現にした場合、交差エントロピー損失とKLダイバージェンスは形式的に一致する。具体的には、one-hot表現の場合、この数式における分布PのエントロピーであるH(P)が0となるので、「KLダイバージェンス」＝「真の分布Pと近似分布Qで表現した交差エントロピー」が成り立つ。

　交差エントロピーの式は、真の分布Pと近似分布Qで表現すると以下のように定義できる（※数学記号の説明は、「KLダイバージェンス」の用語解説で説明済みなので、ここでは割愛する）。この式にあるxは、分類対象となる各クラス（例：「猫」「虎」「ライオン」など）を表す。

　この式は、交差エントロピー損失における「1データ分の損失」に該当する。なお、前述の「多クラス分類のクロスエントロピー損失」の定義と数式では、データごとに損失を出して、それら全ての総和をデータ数で割ることで「平均を取って」いる。その平均計算を外して、1データ分で書けば以下のように表せる。

　既に述べた通り、下記の2点が成り立つため、上の2つの式が同じ意味の式であることが分かる。

　なお、二値分類の式も本質的には同じである。多クラス分類では総和記号Σで全クラスを足しているが、二値分類では2つのクラス（0を基点とするクラスと、1を基点とするクラス）の確率を明示的に加算記号＋で足し合わせたものと考えれば、同様の構造になる。

用途

　交差エントロピー損失は、分類タスクを解くための機械学習モデルの訓練において、最も広く使われている損失関数の一つである。特に、「モデル出力」と「正解ラベル」のズレを自然対数で強調して評価できるため、分類問題において非常に相性が良い（正解クラスの予測確率が低いほど大きな損失となる）。既に説明したものばかりだが、主に以下のような用途で使われている。

• ロジスティック回帰（二値分類）
• ソフトマックス回帰（多クラス分類）
• ニューラルネットワークの損失関数（分類タスク）

API

　主要ライブラリで交差エントロピー損失は、次のクラス／関数で定義されている。

• scikit-learn： 損失関数として呼び出せる関数やクラスは提供されていないが、交差エントロピー損失と同じ数式を用いた評価指標としてlog_loss()関数が用意されている。なお、一部の分類モデル（例：MLPClassifierクラスなど）の内部では、log_loss()関数（＝交差エントロピーと同じ計算）が最適化目的で使用されている
• TensorFlow（2.x）／Keras： BinaryCrossentropyクラス／CategoricalCrossentropyクラス／SparseCategoricalCrossentropyクラスなど、もしくはbinary_crossentropy()関数／categorical_crossentropy()関数／sparse_categorical_crossentropy()関数など
• PyTorch： BCELossクラス／BCEWithLogitsLossクラス／CrossEntropyLossクラスなど、もしくはbinary_cross_entropy()関数／binary_cross_entropy_with_logits()関数／cross_entropy()関数など
• JAX／Optax（JAX用の最適化ライブラリ）： sigmoid_binary_cross_entropy()関数／softmax_cross_entropy()関数／softmax_cross_entropy_with_integer_labels()関数など

「AI・機械学習の用語辞典」

この連載を「連載記事アラート」に登録する New

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう