［活性化関数］シグモイド関数（Sigmoid function）とは？：AI・機械学習の用語辞典

用語「シグモイド関数（Sigmoid function）」について説明。座標点（0, 0.5）を基点（変曲点）として点対称となるS字型の滑らかな曲線で、「0」〜「1」の間の値を返す、ニューラルネットワークの活性化関数を指す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　AI／機械学習のニューラルネットワークにおけるシグモイド関数（Sigmoid function、厳密には標準シグモイド関数：Standard sigmoid function）とは、あらゆる入力値を0.0〜1.0の範囲の数値に変換して出力する関数である。

　図1に示すように、座標点(0, 0.5)を基点（変曲点）として点対称で、S（＝ς：シグマ）字型曲線のグラフになるため、「シグモイド関数」と呼ばれる。

図1　「シグモイド関数」のグラフ

　ニューラルネットワークの基礎となっている情報処理モデル「パーセプトロン」（後日解説）では「ステップ関数」という活性化関数が用いられていた。しかし、「バックプロパゲーション」（後日解説）が登場してからは（本稿で解説している）「シグモイド関数」が活性化関数として使われるようになった。さらに、最近のディープニューラルネットワークでは「ReLU」がよく使われるようになっている。

　バックプロパゲーションの処理過程では、「損失」を微分することになる。その際の、損失の計算項目の一つである「予測値」は、活性化関数を通して計算される。そのため、微分できないステップ関数の代わりに、微分可能（differentiable）な「シグモイド関数」が活性化関数として採用されたというわけである。

　シグモイド関数は現在では、主に分類問題（二値）における出力層の活性化関数として用いられる。その場合、損失関数には（基本的に）交差エントロピー（Cross entropy、後日解説）が用いられる。

　主要ライブラリでは、次の関数／クラスで定義されている。

• TensorFlow（2.x）／Keras： sigmoid()関数など
• PyTorch： Sigmoid クラスなど

定義と数式

　冒頭では文章により説明したが、厳密に数式で表現すると次のようになる。

　eは「オイラー数」*1（Euler's number＝ネイピア数：Napier's constant、自然対数の底）と呼ばれる数学定数の一つで、約2.718281…という無理数（＝小数点以下が無限に続く数）である。オイラー数は、微分計算がしやすいというメリットがある。具体的に上記の数式の導関数（Derivative function：微分係数の関数）を求めると、次のように非常にシンプルな式になる。

*1　似て非なる用語に、オイラー・マスケローニ定数（Euler-Mascheroni constant、オイラーの定数）「γ」があるので、混同しないように注意してほしい。本稿ではEuler's numberとeが結び付くように「オイラー数」と表記したが、日本では「ネイピア数」と呼ぶ方が一般的である。

一般的なシグモイド関数について

　ちなみに冒頭でも説明したように、上記の数式、つまりニューラルネットワークにおけるシグモイド関数とは、厳密には「標準シグモイド関数」という特殊なシグモイド関数のことを指す（また、「標準ロジスティック関数：Standard logistic function」と呼ばれることもある）。参考までに、一般的なシグモイド関数の式を示すと、下記のように表されることに注意してほしい。

　オイラー数eの指数に係数aが追加されているという違いがある。aは「ゲイン（gain）」と呼ばれ、0より大きい数値を指定できる。ゲインの値によって、S字のカーブがきつくなったり緩くなったりする。標準シグモイド関数とは、このゲインがa＝1という「特殊な状態のシグモイド関数」を指すのである。

Pythonコード

　上記の標準シグモイド関数の数式をPythonコードの関数にするとリスト1のようになる。

import numpy as np

def sigmoid(x):
  return 1.0 / (1.0 + np.exp(-x))

リスト1　シグモイド関数のPythonコード例

　オイラー数で簡単に計算するため、ライブラリ「NumPy」をインポートしている。np.exp(-x)というコードがe^−xという数式を表現している。expは、e（オイラー数）を底（base）とする指数関数（exponential function）を意味する。ちなみにオイラー数（＝ネイピア数）自体はnp.eで取得可能である。

　シグモイド関数の導関数（derivative function）のPythonコードも示しておくと、リスト2のようになる。

# ※リスト1のコードを先に記述する必要がある

def der_sigmoid(x):
  return sigmoid(x) * (1.0 - sigmoid(x))

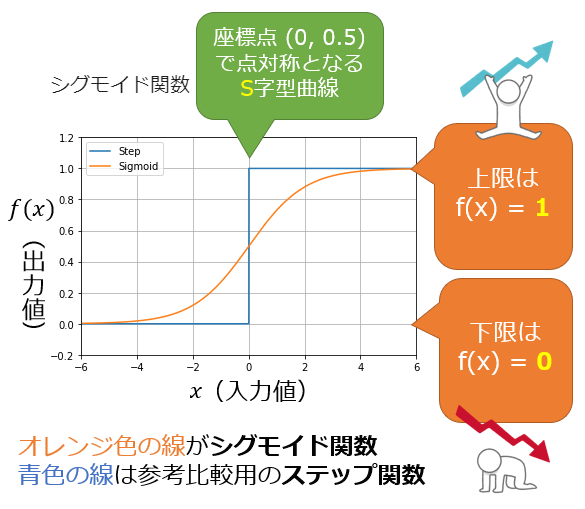リスト2　シグモイド関数の「導関数」のPythonコード例

「AI・機械学習の用語辞典」