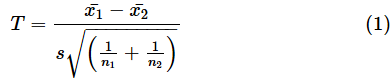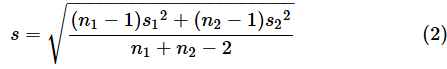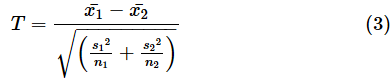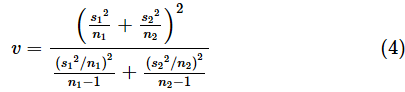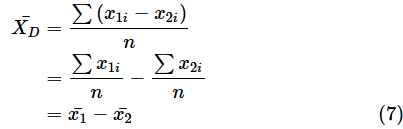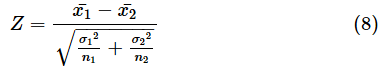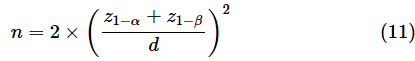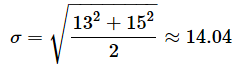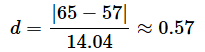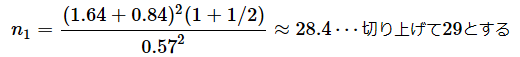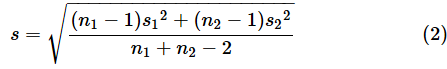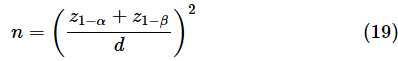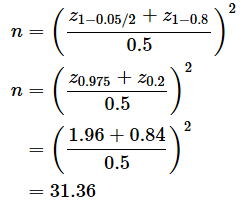【Excelで学ぶデータ分析】学校によって平均点に差があるかを調べたい（t検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第3回。今回は、正規分布する母集団の平均に差があるかどうかを検定する方法について解説します。

» 2025年09月24日 05時00分公開

連載：

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第3回です。前回は、母平均がある値と等しいかどうか（異なるか）を検定する方法を解説しました。今回は正規分布する2つの母集団の平均（母平均）に差があるかどうかを検定する方法を見ていきます。

平均値の差の検定についての基本的な考え方

　前回の「母平均がある値と異なっているかどうかを知りたい」という話（平均値の検定）と、今回の「母平均に差があるかどうかを知りたい」という話（平均値の差の検定）はちょっと似ているので、念のため、その違いを確認することから出発します。それにより、今回の関心事もおのずと明らかになります。

　平均値の検定は、母集団が1つです。ある母集団の平均が何らかの値と等しいか（異なるか）という検定でした。

　今回の平均値の差の検定は、母集団が2つです。それらの母平均に差がないか（差があるか）という検定です。例えば、区間推定編第5回の「私立と公立の中学生で学力テストの差はどれぐらい？」のような事例についての検定となります（図1）。

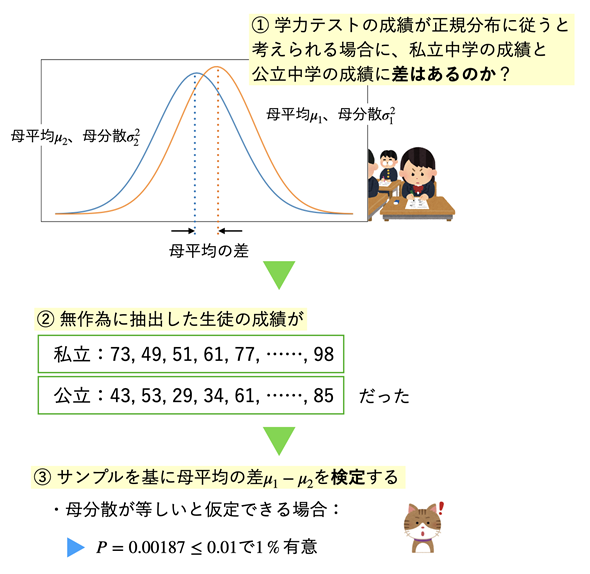図1　私立と公立の中学生に学力テストの差があるかどうか
同じテストを受けた私立の中学生と公立の中学生に成績の差があるかどうかを調べたい。私立の中学生の方が、入学試験を経て一定以上の学力があると認められたと考えられる分、成績が良いものと考えられるので、帰無仮説は「成績に差はない」、対立仮説は「私立の成績の方が良い」となる。それが検証できるのだろうか。

　図1の例では、サンプルとして取り出された中学生は同じテストを受験したものとします。あらかじめお断りしておきますが、この例は検定の計算方法を知るために単純化したものです。国立教育政策研究所の「令和6年度全国学力・学習状況調査報告書【中学校／国語】」のデータを参考にしてはいますが、あくまで架空のデータです。

　サンプルの中学生は、同じテストを受験したものとしますが、それ以外の条件は統制されていません。例えば、生徒の基本的な学力、教員の資質、教科書などの教材の違い、授業の進め方や進度など、さまざまな違いがあるはずです。それらを抜きに「どちらの成績がいい」というのはあまりにも雑な議論であることに注意してください。さらには、検定結果だけを基に「どちらの学校がいい」と評価するのも乱暴です。学力だけでなく、それ以外の活動も含めて、それぞれの良さや課題を評価するのが建設的な考え方だといえます。

　前提として、いずれの母集団も成績は正規分布するものとします。これについても、サンプルサイズがある程度大きければ（一般に30以上といわれます）、母集団が正規分布していなくても、平均値の差の検定ができます。

　平均値の差の検定は、一般にt検定と呼ばれ、ExcelのT.TEST関数を使えば、計算方法を知らなくても簡単にできてしまいます。ただし、以下のような場合をきちんと区別する必要があります。後で具体的な例を見ますが、T.TEST関数の第4引数で指定します。

対応のあるデータの場合：第4引数に1を指定する
対応のないデータ（独立した2群）の場合：
- 母分散が等しいと仮定できる場合：第4引数に2を指定する
- 母分散が等しいと仮定できない場合：第4引数に3を指定する

　それぞれの場合について、帰無仮説を立て、T.TEST関数を使ってP値を求めてみましょう。対応のあるデータの場合は、後で見ることとして、まず、独立した2群について、順に見ていきます。なお、実際にt検定でどのような計算が行われるかについては、T.TEST関数を使って検定を行った後で説明します。

平均値の差の検定での帰無仮説と対立仮説

　図1の例では、以下のような帰無仮説と対立仮説が立てられます。私立の母平均をμ₁、公立の母平均をμ₂とします。

帰無仮説（H₀）：母平均は等しい（μ₁＝μ₂）
対立仮説（H₁）：私立の母平均の方が大きい（μ₁ > μ₂）

　今回の例では、入学試験のある私立中学の方が、受験勉強を経験してきた分、成績がいいと思われるので、対立仮説を「私立の母平均の方が大きい」としました。従って、片側検定を行うことになります。もし、どちらが大きいという仮説が立てられないのであれば、対立仮説は「母平均は異なる」となり、両側検定を行います。

　なお、調査や実験に先立って、サンプルサイズを見積もっておく必要がありますが、それについては最後にまとめておきます。

平均値の差の検定をやってみよう（母分散が等しいと仮定できる場合）

　それでは、平均値の差の検定に取り組みましょう。今回の例では、母分散についてはこれまでの事例や先行研究などがないので、母分散が等しいという仮定はできません。が、検定の手順を見るために、あえて母分散が等しいものとしてやってみます。

　こちらからダウンロードしたExcelファイルを開いて試してみてください。［平均値の差の検定 (等分散)］ワークシートを表示して、セルD4に「=T.TEST(A4:A48,B4:B48,1,2)」と入力するだけです（図2）。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

図2　平均値の差の検定（母分散が等しいと仮定できる場合）
T.TEST関数には、一方のデータの範囲（ここではA4:B48）と、もう一方のデータの範囲（ここではB4:B48）、片側検定を表す1、母分散が等しい場合を表す2を指定する。それぞれのサンプルサイズは異なっていてもよい。

　図2の結果を見ると、P＝0.00187 ≤ 0.01なので、1％有意となり、帰無仮説が棄却されます。

　サンプルファイルの［平均値の差の検定 (等分散・作成例)］ワークシートには、図2の結果と併せて、信頼区間と事後の効果量の計算も含めてあります。信頼区間の求め方はこちらをご参照ください。ちなみに、μ₁－μ₂の95％信頼区間は、2.95 ≥ μ₁－μ₂ ≥ 14.78で、事後の効果量（Cohen's d）は0.628（サンプルの不偏標準偏差を使って計算）となっています。前回もお話しした通り、同様の調査や研究と比較して、信頼区間が狭く、効果量が大きければ対立仮説が強く支持できると考えられます。

　なお、対立仮説がμ₁ < μ₂の場合（公立の平均の方が大きいという仮説の場合）でも、図2で見たT.TEST関数でP値が求められます。両側検定を行う場合は、第3引数に両側検定を表す2を指定します。つまり、「=T.TEST(A4:A48,B4:B48,2,2)」となります。

平均値の差の検定をやってみよう（母分散が等しいと仮定できない場合）

　次に、母分散が等しいと仮定できない場合です。実際には、このような場合が多いと思われます。上で見たT.TEST関数の第4引数に3を指定するだけです。図2で入力した式を変えて「=T.TEST(A4:A48,B4:B48,1,3)」とすればいいですね。サンプルファイルの［平均値の差の検定 (非等分散)］ワークシートを表示し、図3のようにT.TEST関数を入力してみましょう。

図3　平均値の差の検定（母分散が等しいと仮定できない場合）
T.TEST関数には、一方のデータの範囲（ここではA4:B48）と、もう一方のデータの範囲（ここではB4:B48）、片側検定を表す1、母分散が等しいと仮定できない場合を表す3を指定する。それぞれのサンプルサイズは異なっていてもよい。

　P＝0.00188 ≤ 0.01なので、1％有意となり、帰無仮説が棄却されます。なお、サンプルファイルの［平均値の差の検定 (非等分散・作成例)］ワークシートには、信頼区間と事後の効果量の計算も含めてあります。信頼区間の求め方はこちらをご参照ください。

　なお、この場合の検定のことをウェルチの検定と呼びます。

　対立仮説がμ₁ < μ₂の場合（公立の平均の方が大きいという仮説の場合）でも、やはり図3で見たT.TEST関数でP値が求められます。両側検定の場合は、第3引数に両側検定を表す2を指定します。つまり、「=T.TEST(A4:A48,B4:B48,2,3)」となります。

平均値の差の検定をやってみよう（対応のあるデータの場合）

　対応のあるデータとは、同じサンプルから2回取ったデータです。例えば、同じ人が2回テストを受けた場合がそれに当たります。

　この場合、2回の差について、平均値の検定を行います（前回やった平均値の検定です）。帰無仮説は「差の平均は0である」です。これまで見てきた例（独立した2群の場合）は、「平均の差」についての検定でしたが、対応のあるデータの場合は「差の平均」についての検定です。

　つまり、2群の平均を求めてその差が0であるかを検定するというのではなく、個々人の成績の差を求め、それらの平均が0であるかどうかを検定するということです。差の母平均をμ_Dと表すと、以下のように表せます。

帰無仮説（H₀）：差の母平均は0である（μ_D ＝ 0）
対立仮説（H₁）：差の母平均は0でない（μ_D ≠ 0）

　ここでは、1回目のテストと2回目のテストで、成績が良くなると考えられる明確な根拠がないものとします。その場合、対立仮説は、どちらが大きいという仮説ではなく、差がある（＝差の母平均は0でない）という仮説になり、両側検定を行います。つまり、μ_D < 0の場合とμ_D > 0の場合の両方を考える必要があるということです。

　繰り返しになりますが、対応のあるデータの場合、個々人の成績の差が母集団となります。つまり、母集団は1つで、その平均がある値（0）と等しいかどうかを検定する、ということなので、1回目と2回目の成績の差をサンプルとして、前回やった母平均の検定を行うというわけです。

　対応のあるデータのt検定では、T.TEST関数の第4引数には1を指定します。サンプルファイルの［平均値の差の検定 (対応あり)］ワークシートを表示し、図4のようにT.TEST関数を入力してみましょう。それぞれの値は、これまでの例と違って、同じ人が受験した1回目の成績と2回目の成績であるということに注意してください（私立と公立の例は、異なる人が同じテストを受験した値でした）。

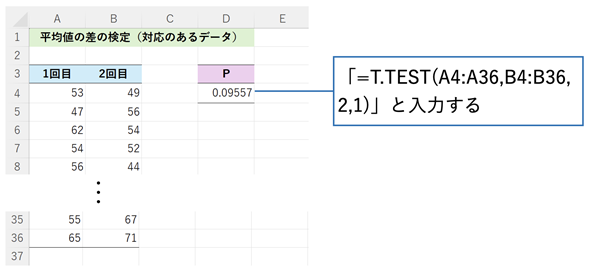図4　平均値の差の検定（対応のあるデータの場合）
T.TEST関数には、1回目のデータの範囲（ここではA4:B36）と、2回目のデータの範囲（ここではB4:B36）、ここでは、両側検定を行うので、第3引数には2を指定し、第4引数には、対応のあるデータを表す1を指定する。対応のあるデータなので、サンプルサイズは同じでないといけない。対応するセルに値が入力されていない場合は、その行は無視される。

　結果は、P＝0.09557 > 0.05なので、有意差は認められませんでした。帰無仮説が棄却されないので、対立仮説を採用するわけにはいきません。従って「1回目と2回目で差があるとはいえない」ということになります。ただし、帰無仮説が棄却されないからといって、帰無仮説が採用される（差はない）とはいえません。なお、サンプルファイルの［平均値の差の検定 (対応あり・作成例)］ワークシートには、信頼区間と事後の効果量の計算も含めてあります。

　学力テストの場合、1回目と2回目で同じテストを使うわけにはいかないので、テストの難易度を等しくするのは難しいです。問題を幾つかのレベルに分けてバランスを取る、などの方法はありますが、完全に統制できているとは言い切れません。従って、差があるという結果が得られたとしても、それだけでは、テストの難易度が変わったのか、生徒の学力が伸びたのかは分かりません。一方、体力テストのような実技テストの場合、1回目と2回目で同じテストができるので、難易度に関しては統制ができます。

コラム　有意差が出なかった！　次のステップは？

　上で見た、平均値の差の検定（対応のあるデータ）では、有意差が出ませんでした。期待した結果が得られず、ちょっと残念ですね。では、次にどのようなことをすればいいでしょうか。まず、やってはいけないことを以下に記します。

後から有意水準を変える： α＝0.01で設計した実験や調査で、実際にサンプルを収集して検定を行った結果がP ≤ 0.01とはならなかったが、P ≤ 0.05になったので5％有意で帰無仮説を棄却する……というのはダメ。ただし、α＝0.05で設計した実験や調査で、結果がP ≤ 0.01となった場合に、「1％有意であった」と言うのは問題ない（基準を緩くするのはダメだが、厳しく見るのは問題ない）
後から両側検定を片側検定に変える：上の例は片側検定だと5％有意になるが、両側検定を行うか片側検定を行うかは、何らかの根拠を基にして、実験や調査などの前に決めておくべき。
後からサンプルを増やす：サンプルを増やすと有意差が出ることがあるが、その場合、検定を2回行うことになり、第一種の過誤の確率を増やしてしまう。

　第一種の過誤を犯す確率を0.05とすると、1回目の検定で第一種の過誤を犯さずに正しく判断できる確率は0.95です。2回目の検定でも第一種の過誤を犯さず正しく判断できる確率も0.95です。とすると、2回の検定でいずれも正しく判断できる確率は0.95×0.95＝0.9025となります。ということは、少なくとも1回、第一種の過誤を犯す確率は1－0.9025＝0.0975となってしまい、誤った判断を行う確率がぐんと跳ね上がるというわけです。

　上で示したような方法で、何とかして有意にしようとすることはP-Hackingと呼ばれ、信頼性を損なう行為として厳に慎むべきとされています（P-Hackingの例は他にもあります。『心理学評論』などで、何回か特集が組まれているので、興味のある方は参照してみてください）。

　では、有意差が出なかった場合、次にやるべきことはどのようなことでしょうか。変に小細工せず「その結果をきちんと受け止める」というのが基本的なスタンスです。同じ仮説の下で、サンプルサイズを増やしてもう一度同じ実験や調査を行っても意味がありません。次にやるべきことは「次の一歩を踏み出す」ことです。

　具体的には、別の仮説を立てるということです。より詳細な、あるいは違った視点からアプローチし、効果の高い介入（例えば、より効果的な授業の進め方）を行うことにより、平均に差があるかどうかを調べる、という流れです。平均の差が大きくなることが確実に期待できるようであれば、（仮説が異なるので）次の検定は片側検定としても構いません。また、最初の方法がうまくいかなかった場合でも、それを捨てて、うまくいった結果だけを報告するのではなく、そこに至る経緯も報告する必要があります（うまくいかなかった方法を知ることも重要ですし、その中にも何らかの注目すべき点があるかもしれません）。

平均値の差の検定ではどのような計算が行われるのか

　では、T.TEST関数でどのような計算が行われているのかを確認しておきます。数式が苦手な方はあまり気にせず、この記事で取り上げたT.TEST関数の形式まで読み飛ばしていただていても構いません。

平均値の差の検定（母分散が等しいと仮定できる場合）での計算

　母平均μ₁、母分散σ₁²の正規母集団と、母平均μ₂、母分散σ₂²の正規母集団があるとき、それぞれの母集団から取り出したサンプルのサイズをn₁,n₂、平均を

とし、不偏分散をs₁²,s₂²とします。母分散が等しいと仮定される、つまり、σ₁²＝σ₂²であると考えられる場合、以下の式で検定統計量Tが求められます。

　ただし、

とします。このとき、検定統計量Tは、自由度n₁＋n₂－2のt分布に従います。この計算は区間推定でも使ったものです。P値は以下のようにして求められます。

対立仮説がμ₁ > μ₂の場合、上記のt分布でTに対する右側確率
対立仮説がμ₁ < μ₂の場合、上記のt分布でTに対する左側確率
対立仮説がμ₁ ≠ μ₂の場合、上記のt分布でTの絶対値に対する両側確率（右側確率×2でも求められる）

　t分布の累積分布関数の値（左側確率）を求めるための式は、かなり複雑なので、ここでは割愛します（確率分布編第8回のコラムで紹介しています）。Excelでは、右側確率はT.DIST.RT関数で、左側確率はT.DIST関数で、両側確率はT.DIST.2T関数で簡単に求められます。

　対立仮説がμ₁ > μ₂の場合について、右側確率を可視化しておきます。（1）式と（2）式で求めた検定統計量Tが2.98、自由度が88だった場合の例です（図5）。

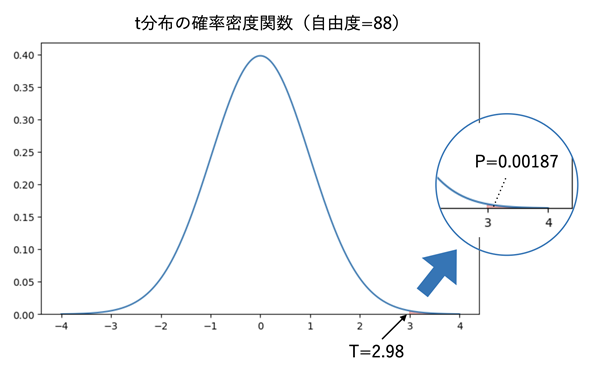図5　検定統計量T=2.98に対するt分布の右側確率
自由度88のt分布の確率密度関数で、T＝2.98点よりも右側（上側）の累積確率（オレンジ色の部分の面積）はP＝0.00187となる。帰無仮説が正しいとすれば、かなり珍しいことが起こった、ということが分かる。

　サンプルファイルの［平均値の差の検定 (等分散・作成例)］ワークシートに、上の手順で計算した例を含めてあります。また、Pythonを使って同様の手順で検定を行い、図5のグラフを描くプログラムもこちらに作成してあります。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行してみてください。コードの詳細については解説しませんが、コード中のコメントを見れば何をやっているのかはだいたい分かると思います。

平均値の差の検定（母分散が等しいと仮定できない場合）での計算

　母分散が等しいと仮定できない場合は、検定統計量Tを以下の式で求めます。

　このとき、検定統計量Tは、以下の式で求められる自由度vのt分布に従います。

　これらの式も、やはり区間推定で使ったものです。

　P値の求め方は、上の「平均値の差の検定（母分散が等しいと仮定できる場合）での計算」の場合と同じです。右側確率はT.DIST.RT関数で、左側確率はT.DIST関数で、両側確率はT.DIST.2T関数で求めるのが簡単です。サンプルファイルの［平均値の差の検定 (非等分散・作成例)］ワークシートに、上の手順で計算した例を含めてあります。

平均値の差の検定（対応のあるデータ）での計算

　最後に、対応のあるデータの場合です。対応のあるデータ同士での差を求めれば、後は、前回の平均値の検定と同じ方法です。

　T.TEST関数では母分散が未知の場合の計算が行われます。平均値の検定（母分散が未知の場合）では、検定統計量Tは以下の式で求められます（前回はtと小文字で表記していましたが、t分布と紛らわしいので大文字で表記します）。

　この式で、

を

とし、μ₀＝0としたものが、対応のあるデータの場合の検定統計量Tとなります。つまり、

です。なお、

は差の平均ですが、実際には平均の差を取っても同じ値になります。

　このとき、検定統計量Tは、自由度n－1のt分布に従います。P値は以下のようにして求められます。

　サンプルファイルの［平均値の差の検定 (対応あり・作成例)］ワークシートに、上の手順で計算した例を含めてあります。

コラム　母分散が既知の場合は?

　T.TEST関数では「母分散が等しいと仮定できる場合」「母分散が等しいと仮定できない場合」、そして、上で説明した「対応のあるデータの場合」の検定ができますが、いずれも母分散が未知の場合の検定です。

　しかし、母分散が既知の場合、つまり「対応のないデータで母分散が既知の場合」「対応のあるデータで母分散が既知の場合」というのも理屈では考えられます。T.TEST関数では、これらの検定はできません。現実には、母分散が既知である場合は考えにくいので、必要となる場面はかなり限られると思われます……が、気になりますよね。検定統計量の求め方と、どのような分布に従うか（標準正規分布であることは想像できると思いますが）だけ紹介しておきます。

◆ 対応のないデータで母分散が既知の場合

　t分布ではなく正規分布を使います。母分散をσ₁, σ₂とすると、検定統計量Zは、

となり、これが標準正規分布に従います。計算例はサンプルファイルの［平均値の差の検定（対応なし・母分散既知）］ワークシートに含めておきます。

◆ 対応のあるデータで母分散が既知の場合

　前回の平均値の検定で、母分散が既知の場合と同じ考え方です。差の平均を

とすると、検定統計量Zは、

となり、これが標準正規分布に従います。計算例はサンプルファイルの［平均値の差の検定（対応あり・母分散既知）］ワークシートに含めておきます。

平均値の差の検定での効果量とサンプルサイズ

　効果量とサンプルサイズの見積もりについて整理しておきます。これについても、検定の種類によって計算方法が異なります。順に見ていきましょう。対応のないデータ（独立した2群）の場合から見ていきます。

2群のサンプルサイズや母分散が等しいと考えられる場合

　まず、Cohen's dと呼ばれる指標を以下の式で求めます。

　μ₁,μ₂は想定される母平均の値、σは既知の母標準偏差または想定される母標準偏差です。過去の調査や経験から、私立の平均が65点、公立の平均が57点、母標準偏差が15点であると見積ることができるのであれば、

となります。各群のサンプルサイズnは以下の式で求めます。2群あるので、2倍します（2群のバラツキがあるので）。

　有意水準をα＝0.05、検出力を1－β＝0.8とすれば、

という結果が得られます。z_0.95≈1.64とz_0.2≈ 0.84という値はExcelのNORM.S.INV関数に0.95や0.2という値を指定するだけで求められます。結果はn＝43.8ですが、小数点以下を切り上げてn＝44とします。両側検定の場合は、z_1－αの代わりに、z_1－α/2を使います。

2群のサンプルサイズや母分散が異なると考えられる場合

　サンプルサイズや母分散が異なる値であると予想される場合には、n₂＝rn₁のように、n₂をn₁のr倍と表して計算します。まず、σとCohen's dを以下の式で計算します。

　続いて、以下のようにして一方のサンプルサイズn₁を求め、n₂をそのr倍とします。

　例えば、私立の平均が65点、公立の平均が57点、母標準偏差がそれぞれ13点、15点と見積もられ、サンプルサイズがn₁, 2n₁と想定されるものとしましょう。つまり、r=2とした場合です。私立の中学よりも公立の中学の方が多いので、サンプルの採りやすさに違いがあることを想定したわけです。上の式で計算すると、

となります。n₁＝n₂である（サンプルサイズが等しい）場合、つまりr＝1の場合で、かつ、σ₁＝σ₂である（母分散が等しい）場合には、（10）式と（11）式での計算と同じになります。

　なお、事後の効果量（実際に実験や調査を行って得られたデータを基に計算する効果量）は、等分散が仮定できる場合は、（13）式のσの代わりに（2）式のs（重み付けした不偏標準偏差）を使い、μ₁－μ₂の代わりに

（サンプルから求めた平均の差）を使ってdの値を求めます。つまり、

　ただし、

とします。等分散が仮定できない場合は、

とします。

対応のあるデータの場合

　既に何度か触れたように、対応のあるデータでのt検定の考え方は、平均値の検定と同じです。従って、以下の式でCohen's dを求め、サンプルサイズnを見積もります。μ_Dは差の母平均、σ_Dは差の母標準偏差（いずれも、何らかの根拠に基づいて想定できる値）です。

となります。両側検定の場合はz_1－αの代わりにz_1－α/2を使います。例えば、μ_D＝5, σ_D＝10の場合、

なので、有意水準をα＝0.05、検出力を1－β＝0.8として、両側検定を行うものとすれば、

となるので、小数点以下を切り上げてn＝32とします。なお、事後の効果量は、

で求めます。x̄_Dはサンプルから求めた差の平均、s_Dは差の不偏標準偏差です。

　母分散が未知の場合は、過去に得られた標準偏差や予備調査で得られた不偏標準偏差をσ₁,σ₂あるいはσ_Dの代わりに使います。正確には、非心t分布と呼ばれる分布を使って計算するのですが、実用的には標準正規分布による近似で十分です。ただし、サンプルサイズが小さい場合（おおむね30未満の場合）は、＋2程度しておくといいでしょう。

　Excelで非心t分布を扱うのは難しいので、Pythonを使ってサンプルサイズを求める例も、検定の可視化と同じファイルに含めてあります。2つ目のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行してみてください。サンプルサイズや母分散が異なると考えられる場合（片側検定）のサンプルサイズとして、n1=28, n2=56という結果が表示されます。また、同様にして3つ目のコードセルを実行すると、対応のあるデータの場合（両側検定）のサンプルサイズとして、n=34という結果が表示されます。

　今回は、母平均の差の検定方法を解説しました。独立した2群では、母分散が等しいと考えられる場合と、母分散が等しいと考えることのできない場合で計算方法が異なり、さらに、対応のあるデータの場合でも計算方法が異なります。T.TEST関数は、その全ての検定に対応しているので、計算方法の違いを意識することなく、引数の指定を変えるだけで、結果が得られます。

　しかし、異なる種類の検定を適用してしまうと、誤った結果となってしまいます。実験や調査の前に、どのようなデータを収集し、どのように分析を行うのかをきちんと計画しておく必要があるというわけです。

　さて、次回は母分散がある値と等しいかどうかを知るための検定（母分散の検定）に取り組みます。どうぞお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。

平均値の差の検定（t検定）を行うために使った関数

T.TEST関数：平均値の差の検定を行う

形式

T.TEST(配列1, 配列2, 尾部, 検定の種類)

引数

配列1： 平均値の差の検定を行うための一方のデータ（サンプル）。
配列2： 平均値の差の検定を行うための他方のデータ（サンプル）。
尾部： 片側検定なら1を、両側検定なら2を指定する。
検定の種類： 以下の値を指定する。
- 対応のあるデータ： 1
- 対応のない（独立した2群の）データ：
  - 母分散が等しいと仮定できる場合： 2
  - 母分散が等しいと仮定できない場合： 3