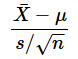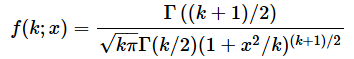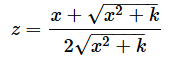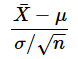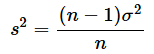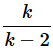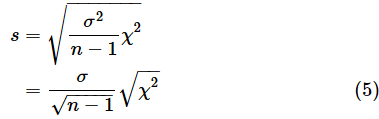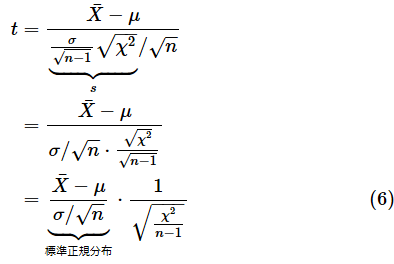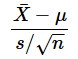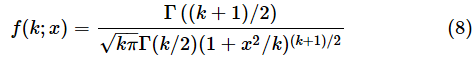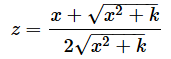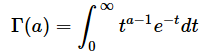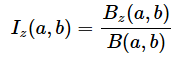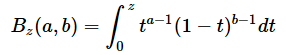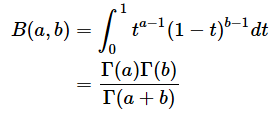［データ分析］t分布 〜 自動車の平均燃費は改善されたか？：やさしい確率分布

データ分析の初歩から学んでいく連載（確率分布編）の第8回。t分布は母分散が分からない場合の平均値に関連する分布です。中心極限定理を出発点とし、正規分布と比較しながらt分布の姿を明らかにしていきます。続けて、確率密度関数や累積分布関数の求め方や可視化の方法を解説し、利用例などを紹介します。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第8回です。前回は、分散に関連する分布として、カイ二乗分布を取り上げました。今回は平均値に関連するt分布について、その特徴や意味を基本から解き明かし、確率密度関数／累積分布関数の求め方、利用例などを見ていきます。

クルマの燃費は改善されたか 〜 t分布の利用

　ある自動車の燃費（燃料1リットルで走行可能な距離）が、平均20kmであったとします。エンジンなどの改良の結果、燃費が改善されたかどうかを知りたい、というのが今回の問題意識です（図1）。類似の事例としては、売り上げが増えたかどうかを知りたい、機器の操作ミスが減少したかどうかを知りたい、固定資産の使用期間が長くなったかどうかを知りたい……などなど、枚挙にいとまがありません。

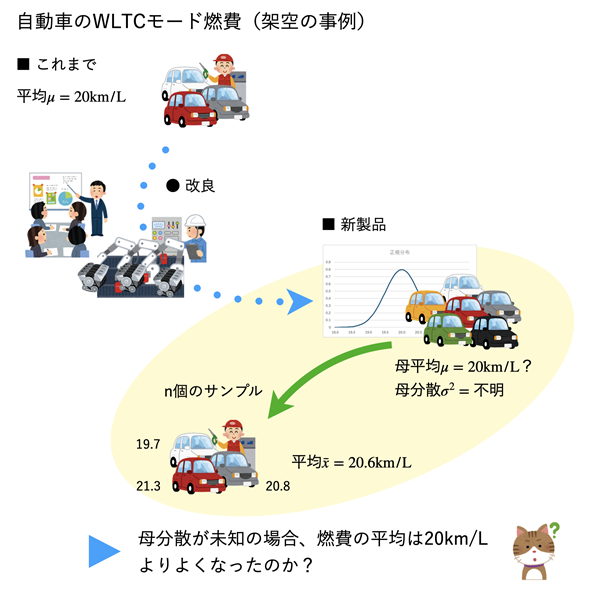図1　母分散が分かっていない場合、母平均がある値よりも大きくなったか？
新製品からn個のサンプルを取り出して燃費を測定した結果から、新製品の母平均がある値よりも大きくなったかどうかを調べたい。母分散が分かっているときには正規分布を使うが、母分散が分からないときはt分布を使う。WLTCモードの燃費とは市街地や郊外、高速道路の走行を想定した（実際の走行に近い）燃費のこと。ちなみに、実際の車種ごとの燃費は国土交通省のサイトでまとめて見られる。

　図1の中で、薄い黄色の背景色を付けたところが今回取り扱う内容です。要するに、幾つかのサンプルを取り出したときに、母平均がある値と異なるかどうか、あるいは、ある値より大きくなったか（小さくなったか）を知りたいということです。結論から先に言うと、母集団の分散が分かっている場合は正規分布を使うのですが、母集団の分散が分かっていない場合はt分布を使います。

　図1に示した問いに答えるには、t分布の確率変数はどのようなものか、t分布の確率密度関数と累積分布関数はどのようなものかを知っておく必要があります。というわけで、ここから少しずつ見ていきます。母分散が分かっている場合と対比しながらお話しするので、正規分布についてのおさらいと補足も含みます。

母分散が分からない場合の平均値に関する分布 〜 t分布の確率変数

　母平均μと母分散σ²が分かっている場合、母集団からn個のサンプルを取り出して

を求めることを繰り返すと、

は平均μ、分散σ²/nの正規分布に近づきます。……という定理の名前は何だったでしょうか。そう、何度も登場した中心極限定理でしたね。

　一応、式で表しておきましょう。確率変数を

とし、正規分布をNと表して、平均と分散をかっこの中に書くと、

となります。∼は「（ある分布に）従う」という意味の記号でしたね。

　では、母集団が正規分布に従っているという前提の下で、母分散σ²が分かっていない場合、サンプルの平均値に関する分布はどのようなものになるでしょうか（図2）。

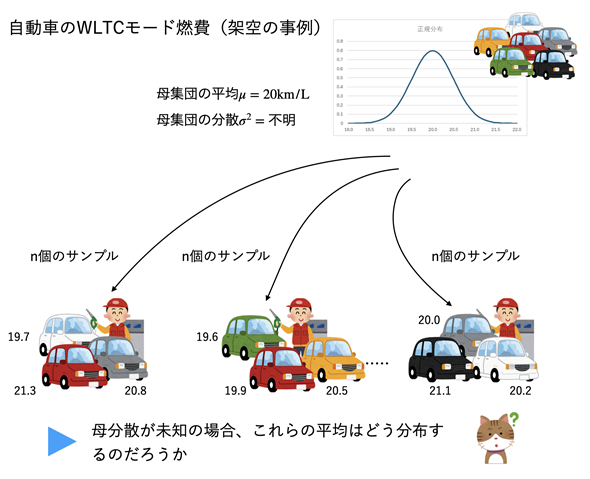図2　母分散が分かっていない場合に、平均値に関する分布は？
母集団が正規分布しているという前提の下で、燃費の平均が20km/Lであるとする。母分散が分かっていない場合には、サンプルから求められた平均値（から求められた確率変数）はどう分布するのだろうか。

　すでに答えはt分布であるとお話ししましたが、t分布は平均値そのものの分布ではなく、平均値を基に求められた確率変数の分布であるということに注意してください。

　端的に言うことにします。母平均μの正規母集団（＝正規分布の母集団）から独立に取り出したn個のサンプルの平均値を

とすると、母分散が分かっていない場合、

という式で表される確率変数は、自由度n−1のt分布に従います。sは不偏標準偏差で、nはサンプルサイズです。自由度とは独立した変数の個数といった意味でしたが、それがなぜn−1になるかは前回詳しく説明したので、そちらをご参照下さい。

　t分布の確率変数がなぜこのような式になるのかは、後の「t分布と標準正規分布の関係」で説明します。ここでは、

がt分布の確率変数になるということだけ確認してください。

　ここまでのお話を∼という記号を使って表すと、以下のようになります。t_(k)は自由度kのt分布です。

　（1）式の左辺が確率変数ですね。この値はt値とも呼ばれます。繰り返しになりますが、t分布は平均値そのものの分布ではないことに注意してください（大雑把に言うなら、母平均と不偏標準偏差を基にサンプルの平均値を標準化した値です）。（1）式の左辺に書かれた確率変数が自由度n−1のt分布に従う、ということですね。

　では、t分布の確率密度関数f(k;x)と累積分布関数F(k;x)はどのようなものでしょうか。一応、数式を掲載しておくと以下のようになります（以下の式では、自由度をk、確率変数つまりt値をxと表記し、;で区切って表しています）。しかし、これらの式を覚える必要は全くありません。ExcelのT.DIST関数を使えば簡単に答えが求められるので、軽くスルーしてください。

　ただし、I_zは正則化された不完全ベータ関数で、

です。……などと言われてもやはり何が何だかですよね。後のコラムでこの定義通りに計算した例も紹介しますが、まずは、ExcelのT.DIST関数を使ってt分布の確率密度関数と累積分布関数を可視化してみましょう。

t分布ってどんな感じの分布（1）〜 確率密度関数を可視化してみよう

　T.DIST関数を使って、t＝−4.0〜4.0に対する確率密度関数の値を求め、グラフを描いてみます。t分布の母数は自由度のみです。つまり、自由度が決まれば、t分布の形も決まります。

　先に、T.DIST関数の形式を見ておきましょう（図3）。

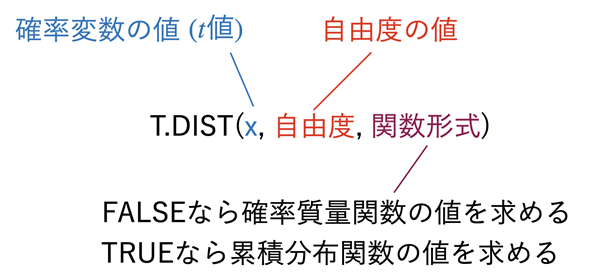図3　T.DIST関数に指定する引数
T.DIST関数には、確率変数の値（t値）と自由度を指定する。関数形式についてはこれまで見てきた関数と同様、FALSEを指定すれば確率密度関数の値が、TRUEを指定すれば累積分布関数の値が求められる。

　図4が、幾つかの自由度に対するt分布の確率密度関数の値を求めてグラフを描いた例です（累積分布関数については次の項で取り扱います）。作成の手順は図の後に記しておきます。

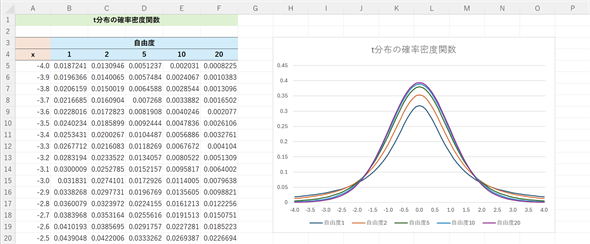図4　t分布の確率密度関数の例
自由度1, 2, 5, 10, 20について、x＝−4.0〜4.0までの確率密度関数の値を求め、グラフを描いてみた。xと表記されているA列の値が確率変数（t値）であることに注意。B〜F列はそれぞれの自由度に対する確率密度関数の値。T.DIST関数を使って確率密度関数の値を求める手順は後の箇条書きを参照。

　t分布の台（確率変数が取り得る値の範囲）は−∞〜∞です。そのうちの−4.0〜4.0の範囲をグラフ化しています。グラフを見ると、x＝0の（つまりt値が0である）位置で山が最も高くなり、左右に裾野が広がる形の分布であることが読み取れます。実は、t分布は、自由度を大きくしていくと、標準正規分布に近づきます。

　確率密度関数の値を求めるための手順は以下の通りです。可視化については単に折れ線グラフを描くだけなので、関数の入力にのみ焦点を当てることにします。グラフ作成の手順についてはサンプルファイル内に掲載しておきます。

　サンプルファイルをこちらからダウンロードし、［t分布］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

◆ Excelでの操作方法

• セルB5に=T.DIST(A5:A85,B4:F4,FALSE)と入力する
  • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB5〜F85）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• セルB5に=ARRAYFORMULA(T.DIST(A5:A85,B4:F4,FALSE))と入力する

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

t分布ってどんな感じの分布（2）〜累積分布関数を可視化してみよう

　続いて、累積分布関数です。こちらは、自由度10の例だけを見ておきます（図5）。確率密度関数でグラフとx軸で囲まれた範囲の面積が累積分布関数の値になることを示すために、確率密度関数も併せて作成し、説明をグラフ上に書き加えてあります。［t分布累積］ワークシートを開き、図の後の手順で試してみてください。グラフ作成の手順についてはサンプルファイル内に掲載しておくこととします。

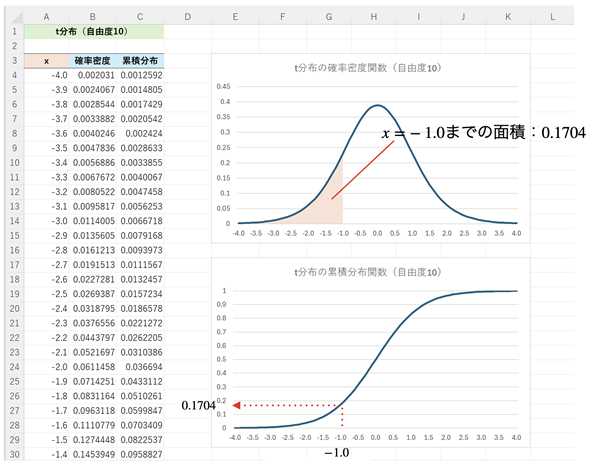図5　t分布の累積分布関数の例
上のグラフが確率密度関数のグラフ。グラフとx軸で囲まれた範囲の面積が累積分布関数の値になる。下のグラフは、その面積、つまり累積分布関数の値をプロットしたもの。例えば、x＝−1.0に対する累積分布関数の値は0.1704となる。

　確率密度関数の値を求める方法はすでに見た通りですが、x＝−4.0〜4.0の範囲を塗りつぶして表示するために使うので、併せて記しておきます。

◆ Excelでの操作方法

• 確率密度関数の値を求める
  • セルB4に=T.DIST(A4:A84,10,FALSE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB4〜B84）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

• 累積分布関数の値を求める
  • セルC4に=T.DIST(A4:A84,10,TRUE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルC4〜C84）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• 確率密度関数の値を求める
  • セルB4に=ARRAYFORMULA(T.DIST(A4:A84,10,FALSE))と入力する

• 累積分布関数の値を求める
  • セルC4に=ARRAYFORMULA(T.DIST(A4:A84,10,TRUE))と入力する

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

本当に燃費は改善されたのか？ 〜 母分散が未知の場合の累積確率を求める

　では、冒頭のお話の続きです。燃費を向上させるためにエンジンの設計などを見直したとします。これまでは燃費が20km/Lでした。改良後、10台のサンプルを取り出して燃費を測定したところ、以下のような値になったとします。

19.7, 21.3, 20.8, 21.4, 20.1, 19.8, 22.1, 21.1, 20.8, 19.9

　これらの値の平均は20.7なので、燃費は改善されたように思われます。……が、そう判断していいのでしょうか。そこで、この場合のt値とt分布の累積分布関数の値を求めてみます。［応用例1（母分散未知）］ワークシートを開いて確認してみましょう（図6）。母平均を20と仮定して、サンプルの平均値からt値を求めてみます。母分散は分からないので（1）式の左辺でt値を求めればいいですね。（1）式を再掲しておきます。手順は図6の後に箇条書きで記しておきます。

　さらに、t値に対する自由度n−1のt分布の累積分布関数の値を求めれば、累積確率が得られます。ただし、ここでは平均値が大きくなったかどうかを知りたいので、T.DIST.RT関数を使って右側確率（上側確率）を求めます。

図6　新しいエンジンの燃費は母平均と等しいか（母分散が未知の場合）
セルD6に=(A16-B3)/(STDEV.S(A6:A15)/SQRT(10))と入力してt値を求める。結果はt＝2.757となる。さらにセルD7に=T.DIST(D6,9,TRUE)と入力してt＝2.757に対するt分布の累積分布関数の値を求めると0.989（＝98.9％）となる。ここでは、平均値が大きくなったかどうかを知りたいので、セルD8に=T.DIST.RT(D6,9)と入力して右側確率を求める。結果は0.0111（＝1.11％）であることが分かる。T.DIST.RT関数では右側確率（右側の累積確率）を求めることが分かっているので、関数形式の引数はない。

　セルD6で求めたt値は（1）式の通りに計算したものです。つまり、サンプルの平均（セルA16）と母平均（セルB3）の差を求め、それを、

で割っています。これが冒頭で見た確率変数の求め方に従って計算したt値です。結果はt＝2.757です。セルD8でこの値に対する右側確率を求めると0.0111（＝1.11％）となります。この結果から、母平均が20であるとすると、取り出したサンプルの平均が20.7であるというのはかなり「まれ」なことであること分かります。つまり、これらのサンプルは平均が20である母集団から取り出されたものではなく、平均がもっと大きい母集団から取り出されたものだ、と言えそうです。というわけで、新しいエンジンの燃費は平均20km/Lよりも大きくなったものと考えられます。

　この例では、セルD7の累積分布関数の値（左側確率）を求める必要はありませんが、参考のために掲載しておきました。なお、両側確率（t値に対する左側確率と右側確率の小さい方の2倍）を求めるT.DIST.2T関数もあります。

　上で求めた右側確率を可視化した図（図7）も［応用例1（母分散未知完成例）］ワークシートに含めてあります。こちらについてはワークシート内に作成方法を記載しておきます。

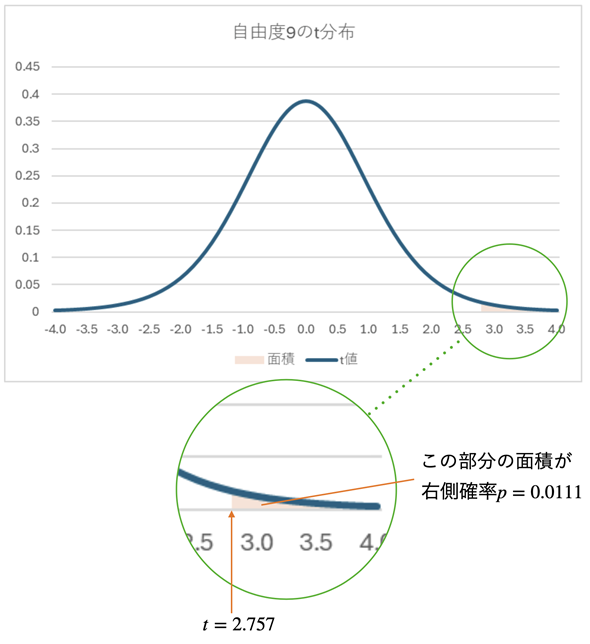図7　t=2.757に対する累積確率
オレンジ色で塗りつぶした部分の面積が右側確率（1.11％）。平均が大きくなるとt値も大きくなるが、t値が2.757になるのはかなり「まれ」なこと（＝確率変数の値がグラフの端の方に位置していて、面積が小さい）。新しいエンジンでは燃費が向上したものと考えられる。

　実は、この計算は母平均の検定のための計算にほかなりません。ただし、帰無仮説や対立仮説などの考え方を十分に知った上で使う必要があるので、この時点で「結論はこうだ！」と言い切るのは少し待ってください。母平均の検定については（さらには平均値の差の検定などについても）、推測統計編でお話しします。

t分布の累積分布関数に対する逆関数は？

　T.INV関数やT.INV.2T関数を使えば、t分布の累積分布関数に対する逆関数の値が求められます。T.INV関数には左側確率と自由度を指定し、T.INV.2T関数には両側確率と自由度を指定します。

　例えば、自由度10のt分布で、累積確率（左側確率）が95％のときのt値は=T.INV(95%, 10)で求められます。結果は1.812となります。

　また、両側確率が5％のときのt値は=T.INV.2T(5%, 10)で求められます。こちらの結果は2.228です。

　空いているセルにこれらの式を入力してみて確認しておいてください。なお、これらの例は［t分布の逆関数］ワークシートに入力されています。t分布の累積分布関数に対する逆関数の値は、母平均の区間推定などに使われます。詳細は推測統計編でお話しします。

　ここまで、t分布の確率変数と確率密度関数、累積分布関数について見てきました。また、応用例として、母平均の検定につながるお話にも（かなり）踏み込みました。ここからは、数式やシミュレーションによってt分布についての理解を深めていきたいと思います。実用的には知らなくてもあまり問題がないので、数式が苦手な方は、最後の「この記事で取り上げた関数の形式」を確認して、今回はお開きとしてもらっても構いません。

t分布と標準正規分布の関係

　最初にt分布の自由度を大きくしていけば、標準正規分布に近づくというお話をしました。それを確かめましょう。中心極限定理を表す式は以下の通りでした。

　N(μ, σ²/n)は平均μ、分散σ²/n（＝標準偏差σ/√n）の正規分布という意味です。上の式を標準化するために、

みましょう。

　この式の意味は、左辺の

という確率変数が標準正規分布に従う、ということですね。

　一方、t分布の定義は（1）式の通りでした。再掲します。

　（1）式と（2）式はよく似ていますね。左辺を見比べると、違いは標準偏差σと不偏標準偏差sだけです。ところで、分散と不偏分散の関係は

なので、nが大きくなると、(n−1)/nが1に近くなります。つまり、不偏分散が分散とほぼ等しくなります。ということは、不偏標準偏差も標準偏差とほぼ等しくなります。というわけで、（1）式のnを大きくしていくと（2）式に近づく（＝t分布で自由度が大きくなると標準正規分布に近づく）ということが納得できると思います。

　t分布の平均（期待値）は0です。t分布は標準正規分布と同様に左右対称の裾野を持ちますが、その山の中心が0になるということですね。自由度をkとすると、「t分布の分散」は

という式で表されます（その導出は本稿では省略します）。kの値を大きくしていくと、この式の分母と分子の差がほとんどなくなって、分散が1に近づくことが分かります。

t分布とカイ二乗分布の関係

　以下のお話は、この時点では特に何かの役に立つわけではありませんが、t分布とF分布（次回取り上げます）の関係を知るのに役立つので、その「伏線」として少しお話ししておきます。数式が苦手な方はあまり気にしなくても構いません。

　すでに何度も登場していますが、（1）式の左辺が自由度n−1のt分布の確率変数でした。それをtとすると、

と表せます。前回、母平均が分かっていないときのカイ二乗値を簡単に求める式として、以下のような式を紹介しました。

　（3）式と（4）式からt分布とカイ二乗分布の関係が分かります。（4）式をs＝の形に変形してみましょう。

　（5）式を（3）式のsに代入して、さらに変形します。

　（6）式の右辺の最初の項は標準正規分布の確率変数です。これをZと置くと、

となります。（7）式がt分布とカイ二乗分布の関係を表しています。もちろん、（3）式で求められるt値と（7）式で求められるt値は一致します。サンプルファイルには幾つかの値を指定して、（3）式の結果と（7）式の結果が一致するかを試した例を［t分布とカイ二乗分布］ワークシートに含めてあるので、興味のある方はご参照ください。

コラム　t分布の確率密度関数をシミュレーションで求める

　すでに何度もお話ししていますが、母分散が分かっていない場合、正規母集団からn個のサンプルを取り出して平均値を求めることを繰り返すと、以下の式で求められる確率変数が自由度n−1のt分布に従います。

　これをシミュレーションしてみましょう。計算を簡単にするために、母集団は標準正規分布であるものとします。標準正規分布であれば母分散がσ²＝1と分かっているのですが、ここでは母分散が分からないものとして、サンプルから求めた不偏分散を使うことにします。

　シミュレーションはExcelでもできますが、多数のセルを使う必要があり、ちょっと面倒です。一応サンプルファイルには作成例（［t分布のシミュレーション］ワークシート）を含めておきますが、ここでは、Pythonのプログラムを使うことにします（リスト1）。

　サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行してみてください。コードの詳細については解説しませんが、コメントとリスト1の説明を見れば何をやっているかが大体分かると思います。

# t分布の確率密度関数のシミュレーション
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm

# 標準正規分布（μ=0、σ^2=1）からランダムに10個のサンプルを取り出したものを10000個作り、平均を求める
x = np.random.randn(10000, 10)
t_mean = np.mean(x, axis=1)  # サンプルの平均
t_std = np.std(x, axis=1, ddof=1)  # サンプルから求めた不偏標準偏差s
t_sample = t_mean / (t_std/np.sqrt(10))  # σではなく、sを使う

# ヒストグラムを描く（t値がどのように現れるかが分かる）
plt.hist(t_sample, bins=100, range=(-4, 4), density=True)  # 階級は100個、縦軸は確率とする

# t分布の確率密度関数を描く
x = np.linspace(-4, 4, 100)  # -4〜4までを100個に分けた等差数列（横軸の値）
plt.plot(x, t.pdf(x, 9))  # xに対するt分布の確率密度関数の値をプロットする
plt.show()

リスト1　t分布の確率密度関数をシミュレーションする
標準正規分布（μ＝0, σ²＝1）からランダムにn＝10個の値を取り出すことを10000回繰り返す。10000行×10列のデータが作られるので、各行の平均を求める。10個のデータの平均が10000個作られることになる。この10000個の平均を基にt値を求める。続いて、縦軸を確率としてt値のヒストグラムを描く。最後に、自由度9のt分布の確率密度関数を描けば、ヒストグラムとほぼ重なることが分かる。

　リスト1の実行例が以下の図8です。乱数を使うので結果は毎回少しずつ異なりますが、ほとんど重なっていますね。

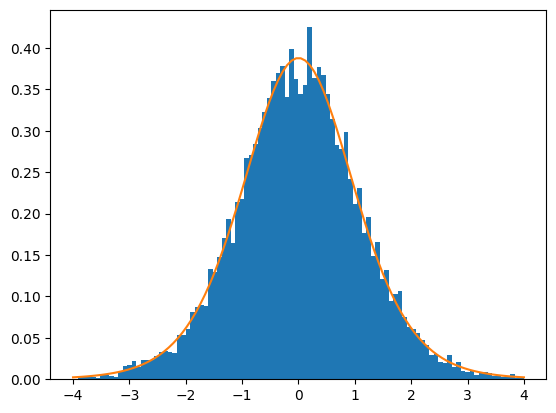図8　t分布の確率密度関数のシミュレーション結果
棒グラフは、標準正規分布から10個のサンプルを10000回取り出し、それらの平均値を基に求めたt値をヒストグラムにしたもの。折れ線グラフは自由度9のt分布の確率密度関数。

コラム　t分布の確率密度関数と累積分布関数を数式で表す

　最初に、t分布の確率密度関数f(x; k)と累積分布関数F(x; k)を表す式を掲載しました。これらの式を覚える必要は全くありませんと言いましたが、もう少し詳しく知りたい方のために、定義通りに計算する方法も紹介しておきます。以下の式では、自由度をk、確率変数つまりt値をxと表記し、;で区切って表しています。

　ただし、I_zは正則化された不完全ベータ関数で、

とします。Γは前回も登場したガンマ関数です。以下にガンマ関数の定義や正則化された不完全ベータ関数の定義を記します（ただし、以下の式のtはt値ではなく、単なる変数です）。しかし、これらの式を使わなくても、Excelの関数だけで（8）式と（9）式の計算ができます。

　ただし、

　（8）式に登場するガンマ関数の値は、ExcelのGAMMA関数で求められます。

　また（9）式に登場する、正則化された不完全ベータ関数I_zは、ベータ分布の累積分布関数と一致します。

　ベータ分布はこの連載では第12回で登場する予定ですが、ExcelのBETA.DIST関数で値が求められます。例えば、自由度が5で、t＝1.5に対する確率密度関数の値を（8）式の定義に従って求めたい場合は、

=GAMMA((5+1)/2)/(SQRT(5*PI())*GAMMA(5/2)*((1+1.5^2/5)^((5+1)/2)))と入力します。結果は0.1245となります。

　一方、累積分布関数の値を（9）式に従って求めたい場合は、BETA.DIST関数にzの値とa＝k/2, b＝k/2の値を指定します。従って、

=BETA.DIST((1.5+SQRT(1.5^2+5))/(2*SQRT(1.5^2+5)),5/2,5/2,TRUE)と入力します。結果は0.9030となります。

　サンプルファイルの［t分布（定義通りに）］ワークシートには上のような値ではなく、セルアドレスを指定して-4.0〜4.0までの確率密度関数の値と累積分布関数の値を求めた例を含めてあります。また、不完全ベータ関数の値を求めるために積分の近似計算を行った例も含めてあるので、興味のある方はご参照ください。もっとも、実用的にはT.DIST関数を使った方が便利ですね。

---

　今回はt分布の確率変数であるt値の意味やその求め方、さらに、t分布の確率密度関数と累積分布関数の求め方などについてお話ししました。推測統計編の内容についても、かなり踏み込んでお話ししてしまいました。t分布は、母平均の区間推定や母平均の検定、平均値の差の検定などに使われますが、ここでは、t分布の確率変数と確率密度関数、累積分布関数についての理解を深めていただければ十分かと思います。

　というわけで、次回は分散の比に関する分布として、F分布についてお話しします。次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

t分布の確率密度関数や累積分布関数の値を求めるための関数

T.DIST関数： t分布の確率密度関数や累積分布関数の値を求める

形式

T.DIST(x, 自由度, 関数形式)

引数

• x： 確率変数の値（t値）を指定する。
• 自由度： 自由度を指定する。
• 関数形式： 以下の値を指定する。
  • FALSE …… 確率密度関数の値を求める
  • TRUE …… 累積分布関数の値を求める

備考

※累積分布関数の値は左側確率（または下側確率）とも呼ばれます。

T.DIST.RT関数： t分布の右側確率の値を求める

形式

T.DIST.RT(x, 自由度)

引数

• x： 確率変数の値（t値）を指定する。
• 自由度： 自由度を指定する。

備考

※1から、T.DIST関数で求められる累積分布関数の値を引いた値が返されます。

T.DIST.2T関数： t分布の両側確率の値を求める

形式

T.DIST.2T(x, 自由度)

引数

• x： 確率変数の値（t値）を指定する。
• 自由度： 自由度を指定する。

備考

※左側確率と右側確率の小さい方の2倍の値が返されます。

t分布の累積分布関数に対する逆関数の値を求めるための関数

T.INV関数： t分布の累積分布関数に対する逆関数の値を求める

形式

T.INV(累積確率, 自由度)

引数

• 累積確率： 累積分布関数の値を指定する。
• 自由度： 自由度を指定する。

備考

※累積確率には左側確率の値を指定します。右側確率に対する逆関数の値を求めたいときには、1−右側確率を指定します。

T.INV.2T関数： t分布の両側確率に対する逆関数の値を求める

形式

T.INV.2T(両側確率, 自由度)

引数

• 両側確率： 累積分布関数の両側確率の値を指定する。
• 自由度： 自由度を指定する。

備考

※例えば、両側確率として5%を指定すると、左側確率が2.5％、右側確率が2.5％となるt値の絶対値が求められます。

「やさしい確率分布」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう