Internet Explorerよりも速くソートできたよ：コーディングに役立つ！アルゴリズムの基本（5）（3/4 ページ）

» 2008年12月03日 00時00分公開

[山下寛人，オイシックス株式会社]

ヒープを配列で実装する

　さて、ヒープは完全二分木なので配列で実装することができます。ルートノードを配列のインデックス1とし、以降左上から順にインデックス2、3、……としていきます。

ルートノードを配列のインデックス1とし、以降左上から順にインデックス2、3、……としていく

　このとき、親ノード・子ノードのインデックスは簡単に計算することができます。あるノードのインデックスをiとすると、


親ノード	i / 2
左の子ノード	i * 2
右の子ノード	i * 2 + 1

となります。

ヒープからソート結果を得る

　では、ヒープからソート結果を得るにはどうしたらよいでしょうか。ヒープではルートノードが最大であることが分かっているので、まずルートノードを取り出します。

　ルートノードを除外した状態でヒープを再構築します。再びルートノードが最大になるのでルートノードを取り出します。これを最後まで繰り返すと大きい順に値が取得できるのでソートできたことになります。

　実際には配列で実装するのでルートノードを取り出したときに末尾のノードと交換します。末尾のノード（配列の要素）はヒープの対象から外し、ルートノードに対して再構築を掛けます。

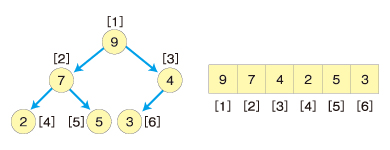
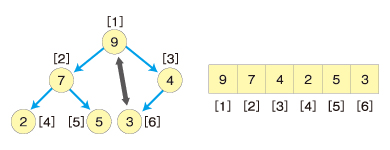
　例を挙げて説明します。ルートノード9と末尾のノード3を交換します。

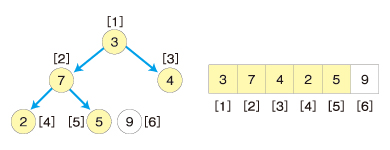
　末尾の要素をヒープの対象から外します。

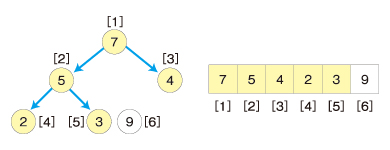
　ルートノードの3を基準にヒープを再構築します。

以後、同様に最後まで繰り返します。

ヒープソートの実装

　解説が長くなりましたがいよいよソースコードの実装です。こちらもマージソート同様、複雑ではありますが、さほどソースは長くありません。再帰を活用しています。

　前のソースコード37行目にある「末尾7」というコメント行の次に以下のコードを追加してください。

<hr/>
ヒープソート<br/>
<span id="heap"></span>
<script type="text/javascript">
Array.prototype.heapSort = function(compare) {
  this.unshift("");
  var middle = Math.floor(this.length / 2);
  for (var i = middle; 1 <= i; i--) {
    this.heapDown(compare, i, this.length - 1);
  }
 
  for (var i = this.length - 1; 1 <= i; i--) {
    this.swap(1, i);
    this.heapDown(compare, 1, i - 1);
    this.display();
  }
  this.shift();
}
 
Array.prototype.heapDown = function(compare, targetIndex, len) {
  var leftChildIndex = targetIndex * 2;
  var rightChildIndex = leftChildIndex + 1;
  var largestIndex;
  if ((leftChildIndex <= len)&&
    (compare(this[leftChildIndex], this[targetIndex]) > 0)) { 
    largestIndex = leftChildIndex;
  } else {
    largestIndex = targetIndex;
  }
  if ((rightChildIndex <= len) &&
    (compare(this[rightChildIndex], this[largestIndex]) > 0)) {
    largestIndex = rightChildIndex;
  } 
  if (targetIndex != largestIndex) {
    this.swap(targetIndex, largestIndex);
    this.heapDown(compare, largestIndex, len);
  }
}
var heap = arrayForDisplay.clone();
heap.view_id = "heap";
heap.display();
heap.heapSort(compare);
var heapForTime = arrayForTime.clone();
func = function() { heapForTime.heapSort(compare); }
time(func, "ヒープソート", "heap");
</script><!-- 末尾8 -->

　プログラムを解説します。

5～18行目

ヒープソート本体です。heapDownメソッドは指定のノードからヒープを再構築するメソッドです。

6行目

配列のインデックスは0から始まりますが、1から始めるようにするために先頭に空の要素を追加しています。

7～9行目

最初にヒープを構築します。末端のノードは除外してもよいため、配列の長さの半分を求め、そこから1に向かってループしながら再構築していきます。

12～16行目

ヒープからルートノードを取り出しながらソートしていきます。

17行目

6行目で追加した空の要素を削除します。

20～38行目