「ビールと紙おむつ」のような相関関係を探る分析手法にはどんなものがある?――データ分析方法についての検討:ITエンジニアのためのデータサイエンティスト養成講座(5)(4/5 ページ)
» 2013年08月22日 18時45分 公開
[中林紀彦,日本アイ・ビー・エム]
(2)分析方法を検討する
では、分析方法の検討をしていきましょう。
まずは、電力使用量を目的変数、最高気温を説明変数とした単回帰分析を用いて相関関係の有無を明らかにしていきます。
電力使用量の方は冷房機器の影響と暖房機器の影響があり、また平日と週末の差が大きいので、冬期と夏期、平日と週末にそれぞれモデルを分けて検討する必要があると思われます。紙幅の都合から、今回は夏期・平日のモデルを検討します。
まずは5月以降の平日のデータに絞り込んだデータセットをそれぞれ作成します(In[26]、In[28])。
In [25]: # 5月以降の平日のデータに絞り込み
In [26]: dfx = df_temp.ix['2013-05-01':'2013-07-25'].resample('B', how='max', kind='period')
In [27]: dfx.plot()
Out[27]: <matplotlib.axes.AxesSubplot at 0x843a690>
In [28]: dfy = df_power_daily.ix['2013-05-01':'2013-07-25'].resample('B', how='max', kind='period')
In [29]: dfy.plot()
Out[29]: <matplotlib.axes.AxesSubplot at 0x85d67b0>
グラフにプロットした結果(グラフ3、グラフ4)を並べてみると電力使用量と最高気温が視覚的にかなり相関がありそうだとうかがえます。
(3)相関関係を確認する
では単回帰分析によるモデルを作成して、モデルに基づく計算結果と比較してみましょう。
In [30]: # 相関関係の分析(モデルの生成) In [31]: model = pd.ols(y=dfy['actual'], x=dfx['high'], intercept=True) In [32]: # モデルに基づく計算値のプロット In [33]: dfy['fit'] = model.y_fitted In [34]: dfy.plot() Out[34]: <matplotlib.axes.AxesSubplot at 0x85d6970>
具体的な中身については次回に詳しく説明することにして、グラフ5に計算値と実測値を並べてプロットしてみましたが、傾向はかなりよく表現できているモデルだと思われます。
Copyright © ITmedia, Inc. All Rights Reserved.
SpecialPR
アイティメディアからのお知らせ
スポンサーからのお知らせPR
SpecialPR
システム開発ノウハウ 【発注ナビ】PR
あなたにおすすめの記事PR

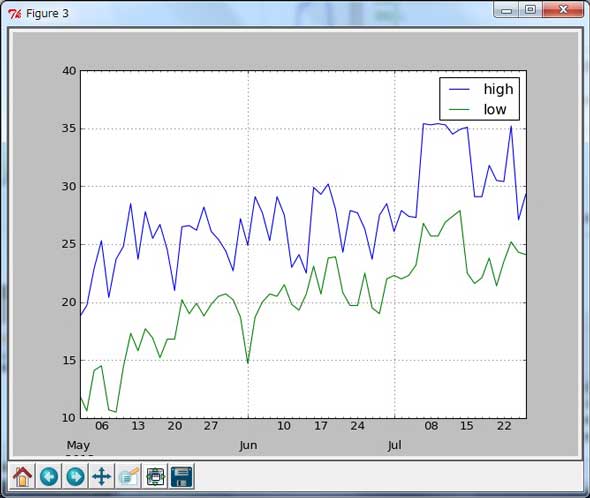 グラフ3
グラフ3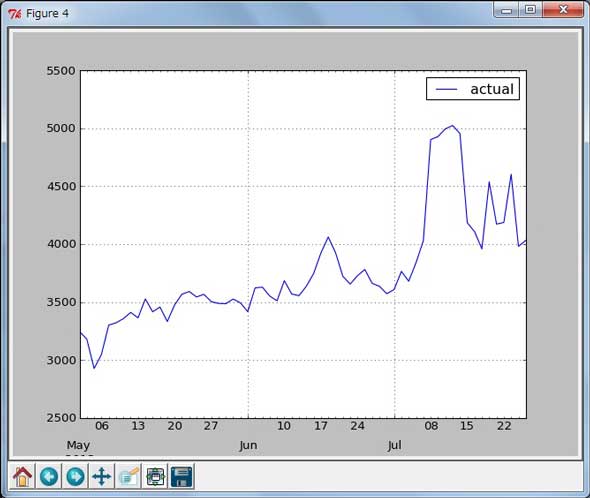 グラフ4
グラフ4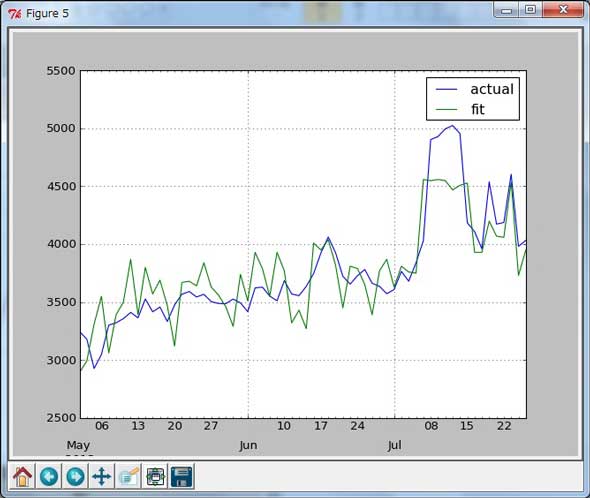 グラフ5
グラフ5



