回帰分析I:回帰分析って何? から、最小二乗法、モデル評価、妥当性検討の実際まで:ITエンジニアのためのデータサイエンティスト養成講座(6)(2/3 ページ)
手順3:回帰分析:仮説の検証
単回帰分析を用いてこのモデル(1)の妥当性を検討してみましょう。
pandasには、こうした目的に便利なols関数が用意されています。
ols関数では
- 目的変数y
- 説明変数x
- 直線が原点(0,0)を通るか切片を持つかどうかのパラメータ(intercept)
を指定すると、先程紹介した最小二乗法(Ordinary Least Squares)を用いてモデル(1)の計算を行います(In [9])。
modelに結果が格納されますので、まずはグラフで計算されたモデルに基づいた直線を確認してみましょう(In [10])。
グラフ2を見ると1m付近の中間部分はよく当てはまっているように見えますが、これは主観的な判断ですので、客観的にモデルの妥当性を判断するために、modelの中身のポイントを確認してみましょう(Out[11])。
In [9]: model = pd.ols(y=weight, x=height, intercept=True)
In [10]: plot(model.x['x'], model.y_fitted, 'g-')
Out[10]:
[<matplotlib.lines.Line2D at 0x87645f0>,
<matplotlib.lines.Line2D at 0x8764970>]
In [11]: model
Out[11]:
Formula: Y ~ <x> + <intercept>
Number of Observations: 1602
Number of Degrees of Freedom: 2
R-squared: 0.8445
Adj R-squared: 0.8444
Rmse: 2.1957
F-stat (1, 1600): 8691.3653, p-value: 0.0000
Degrees of Freedom: model 1, resid 1600
-----------------------Summary of Estimated Coefficients------------------------
Variable Coef Std Err t-stat p-value CI 2.5% CI 97.5%
--------------------------------------------------------------------------------
x 0.0336 0.0004 93.23 0.0000 0.0329 0.0343
intercept -17.2343 0.3742 -46.06 0.0000 -17.9677 -16.5009
---------------------------------End of Summary---------------------------------
modelの出力をみると、係数aはxで示される部分で 0.0336、 定数bは interceptで示される部分で -17.2343 であることが分かります。
つまり、この結果から、モデル(1)の数式は以下のようになります。
[体重]=[身長]×0.0336−17.2343 ――モデル(1)
では、このモデルが統計的にどのくらい正しいのかを検討してみましょう。ポイントは「決定係数」と「F検定」、「t検定」でこの3つの観点から回帰分析のモデルの妥当性を判断します。
(1)決定係数(R-squared: 0.8445)
説明変数が目的変数のどれくらいを説明できるかを表す値で、0〜1の間の値を取り、寄与率と呼ばれることもあります。
今回のモデル(1)では0.8445となっており、このモデルで84%以上説明できているということができます。
(2)F検定(F-stat (1, 1600): 8691.3653, p-value: 0.0000)
F検定(F-test)と呼ばれるモデル全体の妥当性を検討する際に使う値です。F値の有意確率(p-value)を判断基準として用います。
今回のモデル(1)の場合は、F値(8691.3653)が十分に大きく、有意確率(0.0000)も十分に小さく0.01以下であるため99%以上の確率で妥当であると言えます。
有意確率の比較は、99%の場合には0.01ですが、95%の確率で検定する場合には、0.05と比較して妥当性を検証します。
(3)t検定
モデル全体の妥当性をF検定で判断した後は、それぞれのパラメータ(係数aと定数b)の妥当性を検証します。
係数a(x):t-stat=93.23、p-value=0.0000
定数b(intercept):t-stat=-46.06、p-value=0.0000
モデル(1)の場合、xの有意確率もinterceptの有意確率も0.01よりも十分に小さい値なので、両方の値は妥当であると判断できます。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

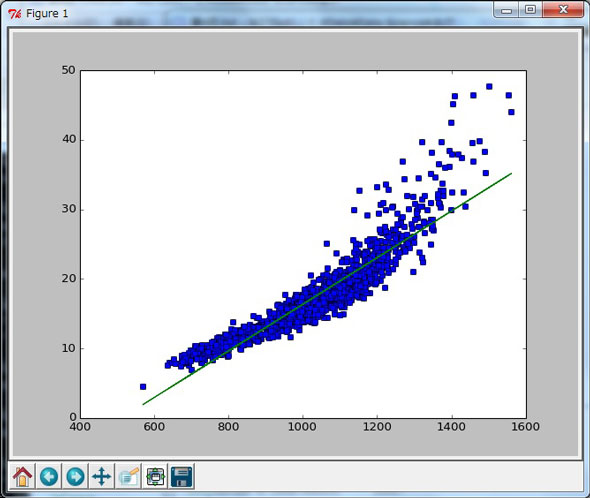 グラフ2
グラフ2



