回帰分析I:回帰分析って何? から、最小二乗法、モデル評価、妥当性検討の実際まで:ITエンジニアのためのデータサイエンティスト養成講座(6)(3/3 ページ)
手順4:モデルの修正:より精度の高いモデルを検討する
前述の3つのポイントからの評価からもモデル(1)でも十分精度のよいモデルだと判断されることがお分かりいただけたと思いますが、もっと精度の高いモデルを作ってみたいと思います。
グラフ2を見ると、身長が低いときの体重の増加量よりも身長が高くなってからの体重の増加量の方が大きく、身長と体重との関係は直線ではなく曲線と仮定することもできます。
確かに“体積は長さの3乗に比例して大きくなる”ということと“重さは体積に比例する”という、物理的な法則を身長と体重の関係に関して当てはめて仮説を見直すと、「体重は身長の3乗に比例する」という仮説を立てることもできます。
[体重]=[身長]^3×[係数a']+[定数b'] ――モデル(2)
このモデル(2)について回帰分析を行い(In [15])、まずはグラフを描画して(In [17])仮説を検証してみると、グラフ3のように身長の3乗と体重がブラフ2よりも直線的になっていて、主観的な判断はあまりよくありませんが視覚的にも結果はかなり良好です。
In [15]: model2 = pd.ols(y=weight, x=height**3, intercept=True)
In [16]: pylab.close()
In [17]: plot(model2.x['x'], model2.y, 'bo', model2.x['x'], model2.y_fitted, 'y-
')
Out[17]:
[<matplotlib.lines.Line2D at 0x89d7b90>,
<matplotlib.lines.Line2D at 0x89d7f50>]
In [18]: model2
Out[18]:
-------------------------Summary of Regression Analysis-------------------------
Formula: Y ~ <x> + <intercept>
Number of Observations: 1602
Number of Degrees of Freedom: 2
R-squared: 0.9002
Adj R-squared: 0.9001
Rmse: 1.7594
F-stat (1, 1600): 14428.5269, p-value: 0.0000
Degrees of Freedom: model 1, resid 1600
-----------------------Summary of Estimated Coefficients------------------------
Variable Coef Std Err t-stat p-value CI 2.5% CI 97.5%
--------------------------------------------------------------------------------
x 0.0000 0.0000 120.12 0.0000 0.0000 0.0000
intercept 5.1931 0.1098 47.31 0.0000 4.9779 5.4082
---------------------------------End of Summary---------------------------------
では客観的にモデル(2)を評価してみましょう。“決定係数”はモデル(1)のときよりも5%以上精度が良い結果になっています。加えて、F検定もt検定も申し分ない有意確率で妥当であるという結果も分かりますので、今回のデータの対象である日本人の満年齢0〜12歳までの子どもにはモデル(2)の方がよく当てはまると言えます。
おわりに
今回は回帰分析について、解法で使われる最小二乗法やモデルの評価、妥当性の検証など基本的なことを紹介しました。
次回は応用編として、回帰分析を「意思決定やアクションにつなげる」ためにモデルを予測に活用する方法や、説明変数が2つ以上のより複雑な重回帰分析などについて詳しく紹介する予定です。次回もお楽しみに。
- 時系列分析II―ARMAモデル(自己回帰移動平均モデル)の評価と将来予測
- 時系列分析I ――ARMAモデルと時系列分析
- 富山県民を分類してみたら……?――クラスタリング分析の手法
- 回帰分析II:重回帰分析の方法、科学的な将来予測
- 回帰分析I:回帰分析って何? から、最小二乗法、モデル評価、妥当性検討の実際まで
- 学習塾を運営するのに最適なのはどこ? オープンデータを活用して実践的なスキルを身に付ける
- 「ビールと紙おむつ」のような相関関係を探る分析手法にはどんなものがある?――データ分析方法についての検討
- ログを分析するには? XMLデータを分析するには? pandasでデータを分析できる状態にする
- データを取り込む・格納するための方法を理解する
- データ分析がデキるITエンジニアになるために必要な「道具」を揃える
- ITエンジニアがデータサイエンティストを目指すには?
Copyright © ITmedia, Inc. All Rights Reserved.

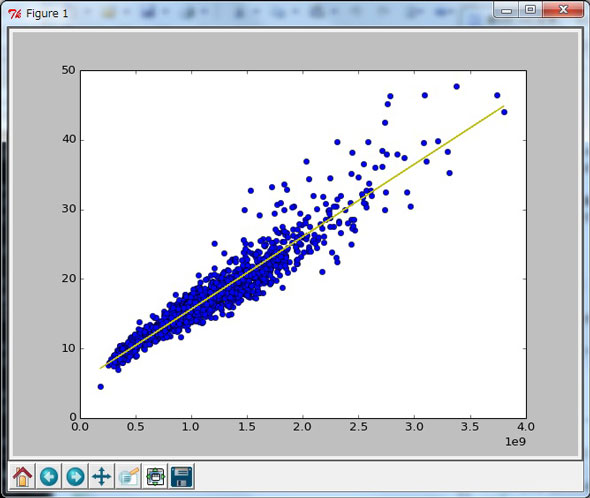 グラフ3
グラフ3



