時系列分析I ――ARMAモデルと時系列分析:ITエンジニアのためのデータサイエンティスト養成講座(9)(3/4 ページ)
AR(1)モデルでの自己相関(Autocorrelation)プロットと偏自己相関(Partial Autocorrelation)プロット
ここからは、「過去の値とどの程度の相関があるか」を定量的に評価するための手法である自己相関(Autocorrelation)プロットと偏自己相関(Partial Autocorrelation)プロットを見てみましょう。
自己相関は、当日以前のデータの影響をどの程度受けているか(相関性があるか)を表すもので、偏自己相関は当日と該当日の2点の間の相関性を表すものです。
(1)のパラメータφ=1.01の時の自己相関と偏自己相関のプロットを見てみましょう(In [30]〜In [37])。
In [28]: # 前のグラフを閉じる In [29]: plt.close() In [30]: # 自己相関(Autocorrelation)プロット In [31]: fig = plt.figure(figsize=(12,8)) In [32]: ax1 = fig.add_subplot(211) In [33]: fig = sm.graphics.tsa.plot_acf(y1.values.squeeze(), lags=40, ax=ax1) In [34]: # 偏自己相関(Partial Autocorrelation)プロット In [35]: ax2 = fig.add_subplot(212) In [36]: fig = sm.graphics.tsa.plot_pacf(y1, lags=40, ax=ax2) In [37]: fig.show()
図4がそれぞれのプロットです。両方とも横軸は「ラグ(lag)値」です。ラグ値の詳細は、参考文献の解説にゆだねますが、ここでは、1日前は「1次のラグ」「2日前は2次のラグ」「n日前はn次のラグ」と表現することを理解しておいてください*。AR(p)のようにpの値が不明な場合には偏自己相関のプロットからpを類推することができます。
* ラグ値は便宜上0から始まっていますが、0次は自分自身との相関なので必ず1になっています。このため、実際には1次以降のラグの部分に着目して見ていきます。図4の場合、偏自己相関はラグ値1(赤枠部分)が有効な値を持っている(=青い部分より値が大きくなっている)ことが分かるので、1つ前のデータ(この場合はAR(1)なので1日前)と大きな相関性を持っていることが分かります。このグラフの読み方については別途解説します。
次ページでは、移動平均 MA(q) モデルについて見ていきます。
Python環境を最新に
Python本体や、幾つかのモジュールがアップデートされていますので、紹介しておきます。ここでは、Windows OS環境を前提に紹介します。他の環境で利用する場合は適宜ご自身の環境に当てはめて読み替えてください。
IPythonはメジャーバージョンアップがあり、パフォーマンスがかなり改善されています。他のモジュールでもパフォーマンスの改善があります。APIの変更があるものもありますから、アップデートの際には注意が必要ですが、影響がなければアップデートしておくことをお勧めします。
IPython
最新のバージョン2.0がリリースされていますので、easy_installコマンドを使ってアップデートします。
C:\>easy_install -U ipython
前のバージョン(1.1.0)からメジャーバージョンアップなので多くの機能追加や改善がされています。変更点や新機能についてはこちらをご覧ください。
pandas:Python Data Analysis Library
最新のバージョン0.13.1がリリースされていますので、easy_installコマンドを使ってアップデートします。
C:\>easy_install -U pandas
pandasの変更点や新機能に関しては、こちらをご覧ください。
NumPy
最新バージョン1.8.1がリリースされています。
ダウンロードしたファイルnumpy-1.8.1-win32-superpack-python2.7.exeを実行すると、インストーラーが起動しますので、ウィザードに従って上書きインストールします。
SciPy
最新バージョン0.14.0がリリースされています。0.13から多くの機能が強化されています。
ダウンロードしたファイルscipy-0.14.0-win32-superpack-python2.7.exeを実行すると、インストーラーが起動しますので、ウィザードに従って上書きインストールします。
Copyright © ITmedia, Inc. All Rights Reserved.

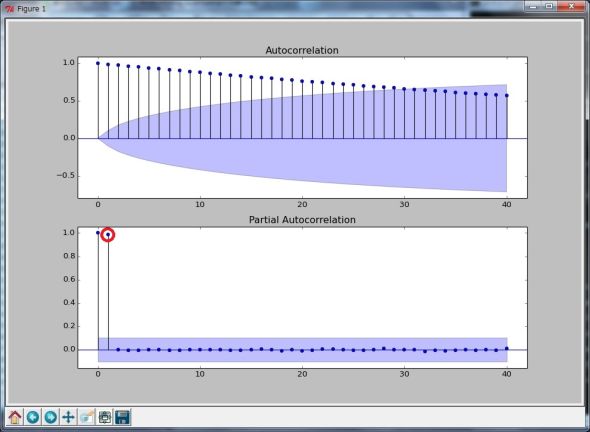 図4 (1)でφ=1.01の時の自己相関と偏自己相関のプロット
図4 (1)でφ=1.01の時の自己相関と偏自己相関のプロット



