時系列分析I ――ARMAモデルと時系列分析:ITエンジニアのためのデータサイエンティスト養成講座(9)(4/4 ページ)
» 2014年06月24日 19時47分 公開
[中林紀彦,日本アイ・ビー・エム]
移動平均 MA(q) モデル
MA(q)モデルは一般的に式2で表すことができるモデルで、一番シンプルなMA(1)モデルでは、「今日の値は1日前の誤差の影響を受ける」というモデルでパラメーターθの符号によって特徴が決定されます。
今回は0.8と−0.8でモデルの特徴を比較してみましょう。
MA(q)モデルはパラメーターの値でどう変わる?(4):θ=0.8の場合
まず、θ=0.8の場合をプロットしてみます(In [40]〜In [45])。
In [38]: # 前のグラフを閉じる In [39]: plt.close() In [40]: # ARパラメーターを設定:今回はMAモデルなのでAR(0)とします In [41]: arparams = np.array([1]) In [42]: # θ=0.8としてサンプルデータを生成しグラフにプロット In [43]: maparams = np.array([1, 0.8]) In [44]: y4 = pd.TimeSeries(arma_generate_sample(arparams, maparams, nobs), index=dates) In [45]: y4.plot() Out[45]: <matplotlib.axes.AxesSubplot at 0x7799890>
MA(q)モデルはパラメーターの値でどう変わる?(5):θ=−0.8の場合
次に、θ=−0.8の場合をプロットしてみます(In [48]〜In [51])。
In [46]: # 前のグラフを閉じる In [47]: plt.close() In [48]: # θ=-0.8としてサンプルデータを生成しグラフにプロット In [49]: maparams = np.array([1, -0.8]) In [50]: y5 = pd.TimeSeries(arma_generate_sample(arparams, maparams, nobs), index=dates) In [51]: y5.plot() Out[51]: <matplotlib.axes.AxesSubplot at 0xafe7f30>
図5がθ=0.8の場合、図6がθ=−0.8の場合のグラフです。この2つを比べるとθが負の値を取ると、グラフの「ギザギザ」の間隔が狭くなっているのが見てとれます。
MA(1)モデルでの自己相関(Autocorrelation)プロットと偏自己相関(Partial Autocorrelation)プロット
それではMA(1)のモデルの自己相関と偏自己相関のプロットを見てみましょう(In [54]〜In[61])。
In [52]: # 前のグラフを閉じる In [53]: plt.close() In [54]: # 自己相関(Autocorrelation)プロット In [55]: fig = plt.figure(figsize=(12,8)) In [56]: ax1 = fig.add_subplot(211) In [57]: fig = sm.graphics.tsa.plot_acf(y4.values.squeeze(), lags=40, ax=ax1) In [58]: # 偏自己相関(Partial Autocorrelation)プロット In [59]: ax2 = fig.add_subplot(212) In [60]: fig = sm.graphics.tsa.plot_pacf(y4, lags=40, ax=ax2) In [61]: fig.show()
ARモデルとは逆に、自己相関のプロットでラグ1の値だけ大きな値を取っています。このようにMA(q)モデルの場合には自己相関プロットからqの値を類推することができます。
おわりに
今回は時系列分析の代表的なモデルの1つであるARMAモデルについて、パラメーターを変化させながらサンプルデータを生成させてモデルの特徴を確認するという、普段とは違ったアプローチでモデルの紹介をしていきました。
次回は実際のデータを使い今回のARMAモデルのパラメーターを推定し、未来の予測に活用するような実例を紹介したいと思いますので、お楽しみに。
Copyright © ITmedia, Inc. All Rights Reserved.
SpecialPR
アイティメディアからのお知らせ
スポンサーからのお知らせPR
SpecialPR
システム開発ノウハウ 【発注ナビ】PR
あなたにおすすめの記事PR

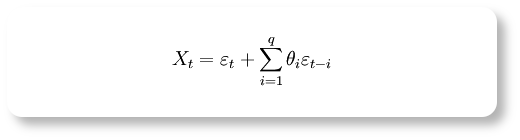 式2(Wikipedia日本語版「
式2(Wikipedia日本語版「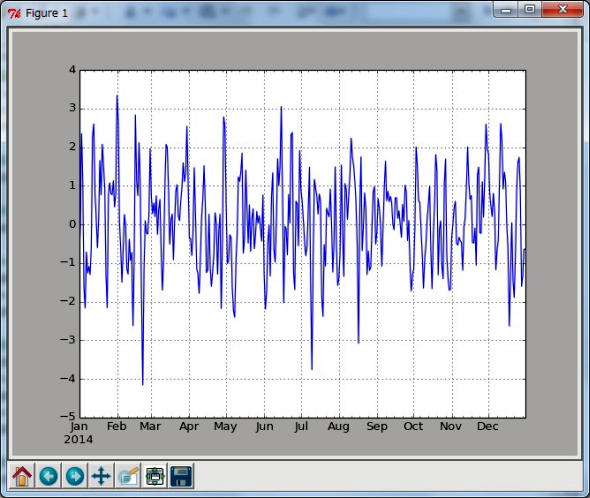 図5 θ=0.8の場合
図5 θ=0.8の場合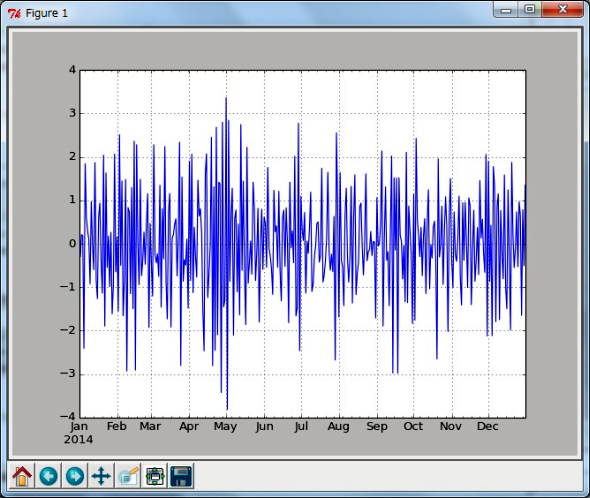 図6 θ=−0.8の場合
図6 θ=−0.8の場合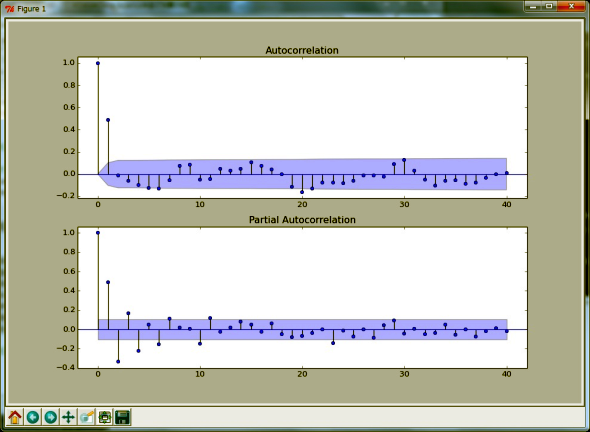 図7 MA(1)のモデルの自己相関と偏自己相関のプロット
図7 MA(1)のモデルの自己相関と偏自己相関のプロット



