データセット、多次元配列、多クラス分類:作って試そう! ディープラーニング工作室(2/2 ページ)
出力層に3つのノードを持たせて、あやめの分類を行う
既に述べた通り、データセットに格納されるデータは一定の形式を持っています。ニューラルネットワークにデータを入力したときに算出されるデータにも一定の形式があります。前回作成したネットワークでは、入力層が4つのノード、隠れ層が5つのノード、出力層が1つのノードを持っていて、ニューラルネットワークモデルに4つのデータを入力すると、値が1つ算出されるようになっていました(実際には、2次元配列となっているデータセットをニューラルネットワークモデルに入力すると、「計算結果を唯一の要素とする配列」を要素とする配列が得られていたことも思い出してください)。
ここで、ネットワークを少しだけ変更して、出力層にノードが3つあるものを考えてみましょう。
なぜ出力が3つかというと、推測するあやめの品種が3種類だからです。出力層から各要素の値がTrue/False(1/0)である配列が出力されるとして、例えばsetosaであれば[1, 0, 0]と、versicolorであれば[0, 1, 0]と、virginicaであれば[0, 0, 1]と出力するようにすることで、3種類のあやめを分類できます。
あやめの品種の推測のように、幾つかの種類(クラス)に分類できるデータが多数あるときに、ニューラルネットワークモデルにそれらの種類を推測させることを「多クラス分類」と呼びます(クラスが3つ以上ある場合。あやめの品種は3つなので、多クラス分類です。2つの種類のどちらであるかを分類することは「2クラス分類」といい、多クラス分類とは区別されています)。このときには、上の図に示したように出力層にはクラスの数に合致するノードを持たせることがよくあります。
このモデルでは、あやめの品種(setosa、versicolor、virginica)に対応するそれぞれのノードから1(に近い値)が、それ以外のノードからは0(に近い値)が出力されるように学習を行うことで、あやめの分類を可能にします。
ところで、このデータセットのtarget属性には整数値が格納されていて、それらは次のような意味を持っていました。
- 0:対応するデータはsetosaである
- 1:対応するデータはversicolorである
- 2:対応するデータはvirginicaである
これらの値(正解ラベル、教師データ)と、ニューラルネットワークモデルの出力(推測結果)の関係を整理すると次のようになります。
- setosaのデータが入力された場合:[1, 0, 0]に近い値が出力されればよい(正解ラベルの値は0)
- versicolorのデータが入力された場合:[0, 1, 0]に近い値が出力されればよい(正解ラベルの値は1)
- virginicaのデータが入力された場合:[0, 0, 1]に近い値が出力されればよい(正解ラベルの値は2)
このとき、正解ラベルは整数値ですが、これは「出力された配列のインデックス」として解釈できます。すると、理想的な出力が得られたときには、正解ラベルが示すインデックス位置にある要素の値だけが1(に近い値)となります。逆に、あまりよろしくない値が得られたときには、正解ラベルが示すインデックス位置にある要素の値は1からは外れた値になります(実際には、Softmax関数を使うことで、配列の要素が0と1の間に収まるようにしていますが、これについては後述の回で取り上げます)。
| 品種 | モデルからの理想的な出力 | 対応する正解ラベル |
|---|---|---|
| setosa | [1, 0, 0] | 0 |
| versicolor | [0, 1, 0] | 1 |
| virginica | [0, 0, 1] | 2 |
| ニューラルネットワークモデルの計算結果と正解ラベルの対応 | ||
このことを利用して、例えばversicolorに対応するデータが入力されたら[0, 1, 0]になるべく近い値([0.04, 0.9, 0.06]など)が得られるように(正解ラベルの値は1)、重みやバイアスを更新することが可能です。つまり、3要素の配列と正解ラベルを比べて、正解ラベルをインデックスとして見たときに、対応するインデックス位置の値をなるべく大きく、それ以外はなるべく小さくするようなニューラルネットワークモデルにするわけです。
コードの詳細な説明は割愛しますが、実際にこれを行うコードを以下に示します。
from sklearn.datasets import load_iris
iris = load_iris()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target)
import torch
X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
y_train = torch.from_numpy(y_train).long()
y_test = torch.from_numpy(y_test).long()
from torch import nn
INPUT_FEATURES = 4
HIDDEN = 5
OUTPUT_FEATURES = 3
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(INPUT_FEATURES, HIDDEN)
self.fc2 = nn.Linear(HIDDEN, OUTPUT_FEATURES)
self.softmax = torch.nn.Softmax(dim=1)
def forward(self, x):
x = self.fc1(x)
x = torch.sigmoid(x)
x = self.fc2(x)
x = self.softmax(x) # softmax関数で配列の要素の総和が1になるように変換
return x
net = Net()
criterion = nn.CrossEntropyLoss() # 交差エントロピー損失を求める関数を利用
optimizer = torch.optim.SGD(net.parameters(), lr=0.3)
EPOCHS = 2000
for epoch in range(EPOCHS):
optimizer.zero_grad()
outputs = net(X_train)
loss = criterion(outputs, y_train)
loss.backward()
optimizer.step()
if epoch % 100 == 99:
print(f'epoch: {epoch+1:4}, loss: {loss.data}')
print('training finished')
for idx, item in enumerate(zip(outputs, y_train)):
if idx == 5:
break
print(item[0], item[1])
values, predicted_idx = torch.max(outputs, 1)
print((predicted_idx == y_train).sum())
基本的な構造は前回に紹介したものと同様ですが、出力層のノード数が3になっていることと(強調書体とした「OUTPUT_FEATURES = 3」行)、これにより出力が3要素の配列(の配列)となるため、クラスのコードや学習の仕方を少々変更しているのが大きな変更点です。具体的には、交差エントロピーと呼ばれる手法で、モデルの計算結果と正解ラベルの誤差を求めているところ、出力層でtorch.nn.Softmaxクラスを使っているところ、最後に計算結果からニューラルネットワークがあやめの品種を推測した結果を取り出す部分などがそうですが、これらについては今回は詳しい説明は省略します。
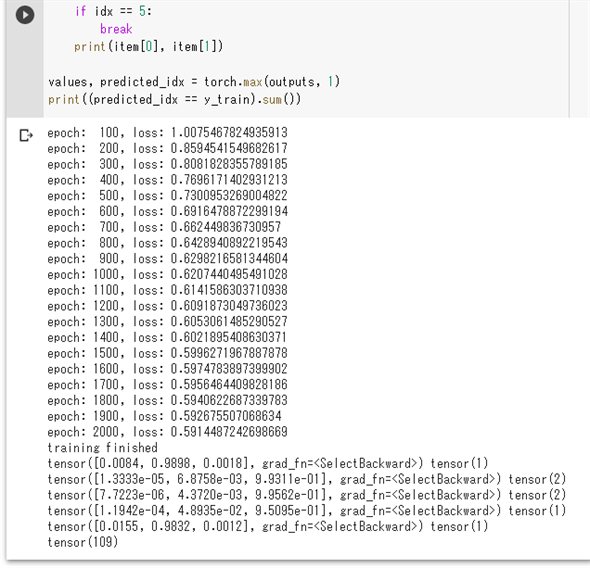
実行結果を以下に示します。
「training finished」の後にあるfor文による出力は、計算結果と対応する正解ラベルの組です。少し読みにくいのですが、3つの浮動小数点数値と、最後にある「tensor(……)」にだけ注目してください。前者がもちろんニューラルネットワークによる計算結果(あやめの品種の推測結果)です。このうち、各行の出力の中に、1にかなり近い値が1個だけあり、他の値はほぼ0になっていることに注目してください。
例えば、最初の行ではインデックス1の要素だけが、1に近い値(0.9898)になっています。モデルがversicolorに対応する[0, 1, 0]という値におおよそ近い値を推測したということです。これに対応する右側の正解ラベルは「tensor(1)」つまりversicolorです。このことから、このデータについてはうまく推測できていることが分かります。他の行の出力についても同様です、といいたいところですが、for文の出力の4行目では、正解ラベルが「tensor(1)」になっているにも関わらず、出力を見るとインデックス2の値が最大になっています。これは推測に失敗していることを表しています。
一番下の行の出力は、112個の訓練データのうち、正しく推測されたものの数の表示です。ここでは109個が一致しているので、上のように間違いはあるものの、よい感じに学習できたと思われます(ここではモデルの評価は省略します)。
最後に、正しい結果が得られたかを計算するときに行っている「values, predicted_idx = torch.max(outputs, 1)」という処理についてだけ、簡単に説明をしておきましょう。これは「outputsの各行(3要素の配列)から最大値とそのインデックスを調べて、それらをタプルにまとめる」という処理を行っています。代入先の変数のvaluesには最大値を要素とする配列が、predicted_idxにはそのインデックス(0〜2)を要素とする配列が返されます。
ここで重要なのは、値そのものではなく、それが3要素の配列の何番目であったかです。例えば、[0.0084, 0.9898, 0.0018]ならインデックス1の要素の値が最大なので、対応するy_trainの要素が1であれば、推測した結果と正解ラベルが等しくなったと考えられます(上のfor文の最初の出力)。そこで、ここではインデックスを格納しているpredicted_idxだけを用いて、その後の処理を行っています。
次の「(predicted_idx == y_train).sum()」という処理では、インデックスの値を含む配列とy_trainの各要素とを比較して、Trueが幾つあったかを数えるだけです(前回にも似たコードを見ました)。こうすることで、モデルが推測した値と、正解ラベルの比較をしています。
今回は前回に紹介したコードや、それを基に少し変更をしたコードを見ながら、データセットや多次元配列の基本的な考え方、データセットの分割では実際には3つに分割することがあること、出力層に3つのノードを持たせた場合のあやめの分類について見てきました。最後に紹介したニューラルネットワーククラス(および前回に紹介したクラス)については、次回に詳しく見ていくことにしましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

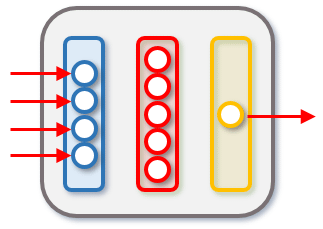 前回作成したニューラルネットワーク(ノードをつなぐエッジは省略)
前回作成したニューラルネットワーク(ノードをつなぐエッジは省略)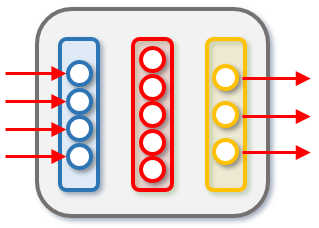 今回作成するニューラルネットワーク(ノードをつなぐエッジは省略)
今回作成するニューラルネットワーク(ノードをつなぐエッジは省略)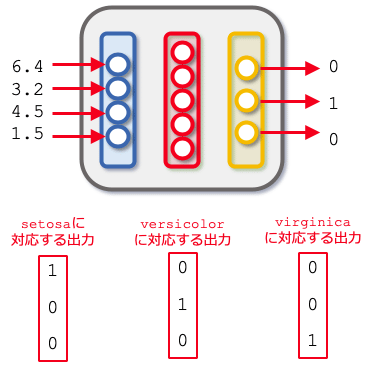 このニューラルネットワークモデルへの入力と出力の例
このニューラルネットワークモデルへの入力と出力の例