自分だけのLinearクラスを作ってみよう:作って試そう! ディープラーニング工作室(2/2 ページ)
出力値を計算するコードを自分で書く
ここでは、MyLinearクラスから少し離れて、重みを格納する行列と同じ5行4列の行列を変数wに、バイアスを格納するベクトルと同じ5要素のベクトルを変数bに、入力値となる4要素からなるベクトルを変数xに代入して、それらを基に出力値を計算してみることにしましょう。それぞれの値には、分かりやすくなるように、浮動小数点数ではなく整数値を用います。
w = torch.tensor([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16],
[17, 18, 19, 20]])
b = torch.tensor([1, 2, 3, 4, 5])
x = torch.tensor([1, 2, 3, 4])
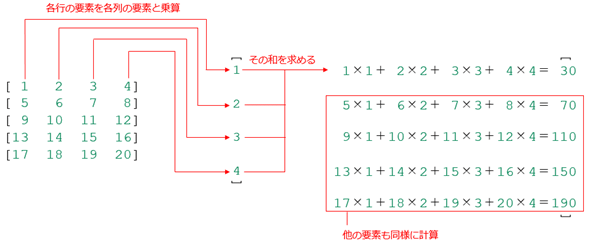
ここで注意したいのは、入力値xと重みwの乗算がどのように行われるかです。簡単にまとめると、重みを格納する行列の各行の要素(4つ)と、入力値xの4つの要素をそれぞれ乗算したものの和にバイアスの値を加算することで、「出力値=重み×入力値+バイアス」という計算が行われます(バイアスも含めて一度の行列演算で全てを計算する方法についても後で見ます)。行列とベクトルの乗算の形で図にすると次のようになります。
上の図では、ベクトルが1行1列の行列のように表されている点に注意してください。このとき、1つ目の行列の各行の各要素を、2つ目のベクトルの各要素と掛け合わせたものの和を要素とするベクトルが計算結果となります。この結果、5要素から成るベクトルが得られるというわけです。
そして、実際にこのような計算を行ってくれるのが、PyTorchが提供するlinear関数なのでした。実際に計算してみましょう。
print(torch.nn.functional.linear(x, w, b))
実行結果を以下に示します。
これと同じ結果を、自分の手で求めるにはどうすればよいでしょう。簡単なのはPythonの@演算子を使うことです。
print(w @ x + b)
実行結果を以下に示します。
同じ結果になりましたね。ところで、今は入力値がベクトル1つだけでした。先ほどの図からも分かるように、このときにはベクトルが1行1列の行列のように扱われ、その要素は縦軸方向に並べられて、重みを格納する行列の行要素とうまいこと乗算されています(この縦軸方向に要素が並べられるのがポイントです。後述)。しかし、ニューラルネットワークには通常、訓練データなどとして多くの入力値(ベクトルを行列にまとめたもの)が一度に渡されます。この場合の計算について少し考えてみましょう。
行列と行列から出力値を計算する方法
以下では、入力値が行列である場合を単純化した例として、入力値xには[1, 2, 3, 4]というベクトルを2つ格納する行列([[1, 2, 3, 4], [1, 2, 3, 4]])が代入されているものとします。イメージとしては、次のような2つの行列から出力値を計算することになります。
このような2つの行列を乗算するにはどうすればよいのでしょうか。実はこれには少し工夫が必要になります。その方法を見る前に、入力値を格納する行列から行単位でデータを取り出す方法を見てみましょう。なぜかといえば、そうすることで、先ほど見た、行列とベクトル(この場合は、入力値を格納する行列の行要素)の乗算に問題を還元できるからです。実際にこれを行うコードを以下に示します。
x = torch.tensor([[1, 2, 3, 4], [1, 2, 3, 4]]) # 入力値xは2行4列の行列
result = torch.zeros(len(x), len(w)) # 2行5列で0を要素とする行列
idx = 0
for item in x:
result[idx] = w @ item + b
idx += 1
print(result)
このコードでは入力値xから1行ずつベクトルを取り出し、それを先ほど見た@演算子を使って「w @ item + b」という計算をすることで、出力値を得て、それを「入力値の行数と同じ行数で(この場合は2)、出力値の数と同じ数だけの列数(この場合は5)」の行列に順次代入していくコードです(torch.zerosメソッドは、指定した行数、列数で要素を0とするテンソルを作成します)。
実行結果を以下に示します。
[1, 2, 3, 4]というベクトルと重みの行列の乗算結果は[31, 72, 113, 154, 195]という5要素のベクトルでした。上のコードではこれと同じベクトルを2つ要素とする行列だったので、これは予想通りの結果といえます。
そして、ここで見た方法よりもスマートに行列と行列を乗算する方法はもちろんあります(NumPyやPyTorchなどのフレームワークは、まさにこのような行列操作=テンソル操作を得意としたフレームワークなのですから)。
行列と行列の乗算の基本
実際にその方法を見ていく前に行列の乗算について簡単に説明をしておきましょう。実は、行列同士の乗算では、「1つ目の行列に格納されている各行の要素と、2つ目の行列に格納されている各列の要素」の乗算が行われます。そして、それらの和を要素とする行列が作られます。言葉では分かりにくいので、簡単な例を示します。
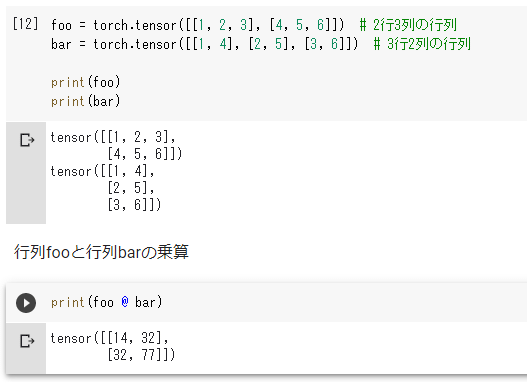
foo = torch.tensor([[1, 2, 3], [4, 5, 6]]) # 2行3列の行列
bar = torch.tensor([[1, 4], [2, 5], [3, 6]]) # 3行2列の行列
print(foo)
print(bar)
ここでは、2行3列の行列fooと3行2列の行列barを作成しています。これらの乗算がどう行われるかを以下に示します。
行列fooと行列barの乗算は、行列fooの各行の要素と行列barの各列の要素を乗じた値の和を要素とした2行2列の行列を生じるということです(上の図では明示していませんが、行列fooの1行目と行列barの2列目でも同様に計算が行われ、それが結果として得られる行列の2行2列目の値となります。行列fooの2行目と行列barの1列目も同様で、これが結果として得られる行列の2行1列目の値となります)。実際にコードで試してみましょう(ここではPythonの@演算子を使用します)。
print(foo @ bar)
実行結果を以下に示します。
重要なのは、行列fooの列数と、行列barの行数が一致していることです。そうでないと行列同士の乗算ができません。これが行列同士を乗算する際の基本です。
重みを格納している行列と入力値を格納している行列の乗算
基本を見たところで、大本の問題に立ち返りましょう。ここでは、次のような行列同士の乗算を行うことが目的でした。
しかし、この2つの行列では重みwの列数が4であるのに対して、入力値xの行数は2となっています。これでは乗算できないのは既に述べた通りです。加えて、行列と行列の乗算では1つ目の行列に格納されている各行の各要素が、2つ目の行列に格納されている各列の各要素と掛け合わされるのでした。ところが、入力値を格納する行列では、重み行列の行要素と掛け合わせたい要素が縦軸方向ではなく、横軸方向に並んでいます。
つまり、ここで行いたいのは、実は重みを格納している行列の行要素と、入力値を格納している行要素の乗算です(行列とベクトルの乗算ではこれが自然と行えていたということです。縦軸方向にベクトルの要素が並んでいたことを思い出しましょう)。
逆にいえば、入力値が行列のときには、行と列を入れ替えることで、うまく計算ができそうです。行と列を入れ替えるとは、この場合、2行4列だった行列を、4行2列の行列にして、縦軸/横軸を入れ替えて、要素を並べ替えるということです。以下に例を示します。
このような、元の行列から行と列を入れ替えた行列のことを「転置行列」と呼びます。そして、転置行列を得るには、PyTorchのテンソルが持つ属性Tを利用できます(この「T」は転置行列を意味する「Transposed Matrix」からきています)。実際に試してみましょう。
print(x)
print(x.T)
実行結果を以下に示します。
2行4列の行列だったのが、4行2列の行列に転置できたのが分かります。これと5行4列の行列である重みwであれば、次のように計算できるでしょう。
print(w @ x.T)
しかし、実行結果を見てください。
この結果は望んでいたものではありません(欲しいのは2行5列の行列です)、バイアスbとの加算も無理です。もちろん、この結果に対して、さらに行と列を入れ替えてもよいのですが、重みwの方を転置してみましょう。
print(w)
print(w.T)
print(x @ w.T)
print(x @ w.T + b)
ここでは入力値xが@演算子の前に、重みwの軸を入れ替えたものが後に置かれていることにも注意してください。これにより、次のような行列同士の乗算が行われることになります。
これなら、1つ目の行列の列数と、2つ目の行列の行数が同じなので、うまく乗算できるはずですし、最初に見た行列とベクトルの乗算で行っていたものと同様な計算が行われる(=出力値がきちんと計算できる)ことも分かります。計算結果は5要素のベクトルを要素とする行列となるので、バイアスの加算も可能です。
実行結果を以下に示します。
うまくいっていることが分かります。
実際に、forwardメソッドにこの結果を組み込むと次のように書けます。
import torch
from torch import nn
from math import sqrt
class MyLinear(nn.Module):
def __init__(self, in_features, out_features):
super().__init__()
self.in_features = in_features
self.out_features = out_features
k = 1 / in_features
weight = torch.empty(out_features, in_features).uniform_(-sqrt(k), sqrt(k))
self.weight = nn.Parameter(weight)
bias = torch.empty(out_features).uniform_(-k, k)
self.bias = nn.Parameter(bias)
def forward(self, x):
#result = torch.zeros(len(x), self.out_features)
#idx = 0
#for item in x:
# result[idx] = self.weight @ item + self.bias
# idx += 1
#return result
return x @ self.weight.T + self.bias
#return torch.nn.functional.linear(x, self.weight, self.bias)
コメントアウトした形で、先ほどの行ごとにデータを抜き出して計算するコードも含めてあります。興味のある方は、こちらのコードも試してみてください。
バイアスを重みに含めて行列の乗算を行ってみる
最後に、バイアスを行列演算に含める方法についても見ておきましょう。ざっくりとした話になりますが、重みの1つの要素としてバイアスを捉え、それに常に入力値1を乗じることで、重みと入力値の乗算結果にバイアスの値を加算するのではなく、行列の乗算にバイアスを含めることが可能です。
実際のコードを以下に示します。
w2 = torch.cat([b.unsqueeze(0), w.T])
ones = torch.full((len(x), 1), fill_value=1, dtype=torch.long)
print('w2:', w2)
print('ones:', ones)
x2 = torch.cat([ones, x], dim=1)
print('x2:', x2)
詳しい説明は省略しますが、変数w2の内容は重みwの転置行列の先頭にバイアスbを付加したものです。変数onesには、入力値xの行数と同じ行数で、列数が1の行列(その値は全て1)が代入されます。変数x2には、変数xの第1列の前に変数onesの行列を付加したものが代入されます。これにより、以下に示す実行結果のような行列が得られます。
バイアスの要素が新しい重みw2の先頭行にあること、新しい入力x2の先頭に1が追加されていることを確認してください(添字を使ってバイアスを表すときにはよくw0のように、またこれと乗じられる値1(入力値)はよくx0のように表現されることがあります。ここでは、これに合わせて、インデックス0の位置にこれらを挿入しています。もちろん、それぞれの末尾にこれらを追加するやり方もあるでしょう)。先ほど見た「出力値=入力値×重み+バイアス」という計算は、実はこのようにすることで、一度の行列演算「入力値×重み」という計算にまとめることができます。例えば、入力値x2の最初の行と重みw2の最初の列との乗算であれば、その計算は次のようになります。
- 1×1+1×1+2×2+3×3+4×4
これを計算すると「1+1+4+9+16」で「31」となります。これまでに計算してきた「出力値=重み×入力値+バイアス」と同じことが行われていることに注目してください(ただし、バイアスを含んだ計算を行う項が最初にあります)。
実際にそうなるかどうかを実際に試すコードが以下です。今度は重みw2は既に転置行列となっているので、属性Tで転置行列を得ていないことには注意してください。
print(x2 @ w2)
実行結果を以下に示します。
これまでと同様な結果が得られたことから、重みと入力値を表す行列の乗算の中にバイアスが含まれたことが分かりました。
今回は、全結合を行うクラスを自分で作りながら、そこで実際にどんな処理が行われているのかを見てきました。あやめのデータセットを扱う例は今回で終わりとして、次回はMNISTを用いた画像認識の手順を見ていくことにしましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 実行結果
実行結果 実行結果
実行結果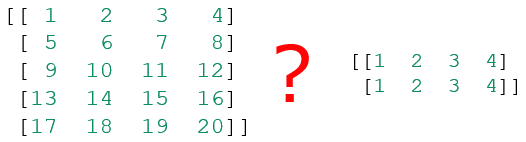 行列(重み)と行列(入力値)の乗算
行列(重み)と行列(入力値)の乗算 実行結果
実行結果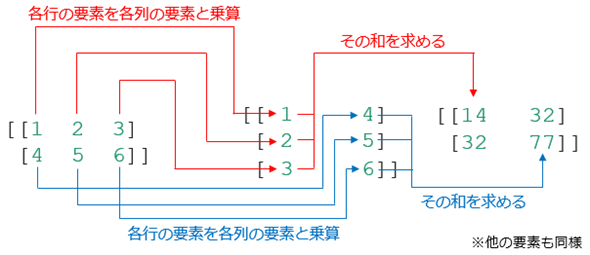
 実行結果
実行結果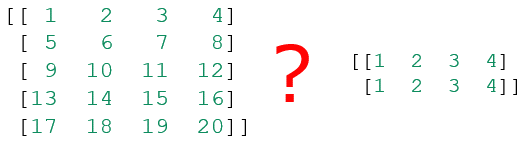 重みを格納する5行4列の行列と、入力値である2行4列の行列では、前者の列数と後者の行数が異なるので乗算ができない(再掲)
重みを格納する5行4列の行列と、入力値である2行4列の行列では、前者の列数と後者の行数が異なるので乗算ができない(再掲) 5行4列の行列と2行4列の行列の乗算
5行4列の行列と2行4列の行列の乗算 実行結果
実行結果 実行結果
実行結果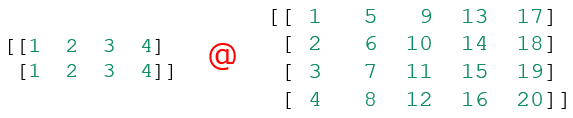 2行4列の行列と4行5列の行列の乗算
2行4列の行列と4行5列の行列の乗算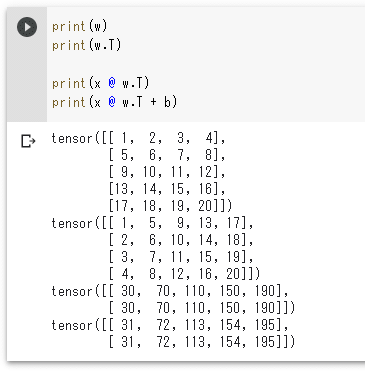 実行結果
実行結果 実行結果
実行結果 実行結果
実行結果



