CNNなんて怖くない! コードでその動作を確認しよう:作って試そう! ディープラーニング工作室(2/2 ページ)
畳み込みとプーリング(2回目)
ここで注意することがあります。それは、先ほどの畳み込みとプーリングで得られた結果の形状です。1回目の畳み込みではカーネル(チャネル)が2つあったので、特徴マップは1つのデータについて2つ得られていました。これは、畳み込みへの入力チャネルが今度は2つあるということです。実際に確認してみましょう。
print(pooled1.shape)
実行結果は次のようになります。
これは「3×3のサイズ、チャネル数が2のテンソル」を4つ格納するテンソルということです。そこで、2回目の畳み込みを行うConv2dクラスのインスタンス(「conv2」としましょう)は次のようにして生成することになります。ここでは、conv1オブジェクトと同様に、カーネルは2つ、パディングを付加、バイアスはなしとしています。
conv2 = torch.nn.Conv2d(2, 2, 3, padding=True, bias=False)
print(conv2.weight.shape)
このときには、カーネルの形状についても注意が必要です。実行結果を見てください。
最初のカーネルの形状は「torch.Size([2, 1, 3, 3])」、つまり「3×3のサイズでチャネル数が1のテンソルが2つ」となっていましたが。この実行結果が意味するのは、2回目の畳み込みで使うカーネルは「torch.Size([2, 2, 3, 3])」、つまり「3×3のサイズでチャネル数が2のテンソルが2つ」です。入力するチャネルの数に合わせて、カーネルのチャネル数も2つとなるわけです。2回目の畳み込みでどのようなカーネルを作ればよいかの判断は難しいのですが(だからこそ、CNNではそうしたものを自動的に作成してくれるともいえるでしょう)、ここでは上で見た特徴に合わせて、横線と縦線を表すものを重複して指定しておきましょう(実際に学習をさせると全く別のカーネルが得られるのではないかと、筆者は予想しています)。
kernels2 = torch.tensor([
[[[-1., -1., -1.],
[ 1., 1., 1.],
[-1., -1., -1.]],
[[-1., -1., -1.],
[ 1., 1., 1.],
[-1., -1., -1.]]],
[[[-1., 1., -1.],
[-1., 1., -1.],
[-1., 1., -1.]],
[[-1., 1., -1.],
[-1., 1., -1.],
[-1., 1., -1.]]]])
print(conv2.weight.shape)
conv2.weight.data = kernels2
1つ目のカーネルは横線を表すテンソルを2つ重複させています。2つ目は同様に縦線を表すテンソルを重複させています(もしかしたら、カーネルは1つで、それぞれのチャネルに横線と縦線を表すものを指定するとよかったのかもしれませんが、ここではこのまま進めましょう)。
実行結果を以下に示します。カーネルの形状が上で見た重みの形状と一致していることを確認してください。
この点以外は、これまでと同様なので、以下では一気にコードを実行してしまいましょう。途中経過が気になる方はコメントアウトしている行を適宜実行して、特徴マップやそれらを活性化関数に通した結果を確認してください。
f_map2 = conv2(pooled1) # 畳み込み
#print(f_map2)
f_map2 = torch.nn.functional.relu(f_map2) # 活性化関数
#print(f_map2)
pooled2 = pool(f_map2) # プーリング
print(pooled2)
実行結果を以下に示します。
今度は2×2のテンソル2つが組になった結果が得られました。実際には、これらを全結合層へ入力することで、それらが横線なのか、縦線なのかの推測が行われるということです。そこで、全結合層へ入力しやすいように、その形状を変更しておきます。
print(pooled2.shape)
pooled2 = pooled2.reshape(-1, 2 * 2 * 2)
print(pooled2)
実行結果を以下に示します。
実行結果を見ると分かりますが、元は「2×2のサイズ、チャネル数が2のテンソルが4つ」だったものを上のコードではこれを2次元のデータに展開しました(reshapeメソッドに指定している引数は「任意の要素数, チャネル数×行数×列数」を意味します)。つまり、4×8のサイズのテンソルになっています。この8個の数値が1つのデータがどんな特徴を持つかを示すデータ「特徴量」と呼ばれるものです。
最初の行と3行目のデータは前半4つのデータに大きな数値が含まれています。これらは横線を示すデータだったので、1つ目のカーネルでの調査結果である前半に強い数値が出ているということです。2行目は縦線なので、その逆になっています。これらのことから、横線と縦線では多くの場合、このような特徴がよく見られることが示唆されます(ただし、畳み込みとプーリングの結果によっては、上の傾向とは異なる特徴量が得られることもあります。そうした要素も含めて適切に推測できるように、横線/縦線の推測を行う全結合層では重みとバイアスの学習が行われます)。
ここであやめの品種の分類のことを思い出してください。あやめの品種の分類では、あやめの品種を表す特徴量は既にデータセットとして用意されていました。しかし、前回のCNNによる手書き数字の認識や今見たような横線、縦線の畳み込み/プーリングでは、特徴量をCNNによって取り出していると考えられます。さらにいえば、特徴量を取り出すために必要な重み(やバイアス)も学習を通して自動的に得られます。ニューラルネットワークの大きなメリットがここにあるといえます(ここでは重みは筆者による決め打ちでしたが)。
大量のデータから人が、特徴量が見つけ出したり、それを見つけるための重みやバイアスを決定したりするのは非常に難しいことですが、ニューラルネットワークはそれらを自動的に行ってくれるのです。
後はこれを(適切に重みとバイアスを学習済みの)全結合型ニューラルネットワークに入力することで、4つのデータが横線なのか縦線なのかを判断できるということになります。
全結合型のニューラルネットワークへの入力
というわけで、先ほど得た4つのデータ(特徴量)を全結合型のニューラルネットワークに入力するのはよいのですが、ここまでの話では元のデータが4つしかありません(というか、それらが何を表すものかを推測するニューラルネットワークを作ろうというのですから、本来、それら4つのデータを使うわけにはいきません)。
そこで今見た4つのデータとは別に40個のデータを作って、そこから40個の特徴量を得た上で、それらを基に学習を行う全結合型のニューラルネットワークをやっつけで作成しました。ここからは本筋とはあまり関係ないので、サクサクと飛ばしていきます。完全なコードと実行結果は公開しているノートブックを参照してください。
inputs = torch.tensor(
[[[-1., -1., -1., -1.],
[ 1., 1., 1., 1.],
[-1., -1., -1., -1.],
[-1., -1., -1., -1.]],
[[-1., 1., -1., -1.],
[-1., 1., -1., -1.],
[-1., 1., -1., -1.],
[-1., 1., -1., -1.]],
# 省略
[[-1., -1., 1., -1.],
[-1., -1., 1., -1.],
[-1., -1., -1., 1.],
[-1., -1., -1., 1.]],
[[ 1., -1., -1., -1.],
[ 1., -1., -1., -1.],
[-1., 1., -1., -1.],
[-1., -1., 1., -1.]]])
labels = torch.tensor([
0, 1, 0, 0, 1, 0, 0, 1, 0, 1,
1, 0, 1, 0, 1, 1, 0, 1, 0, 0,
1, 1, 0, 1, 0, 0, 1, 1, 0, 1,
0, 0, 1, 0, 1, 0, 1, 0, 1, 1
], dtype=torch.float)
先ほどと同じ手順で、これらのデータから40個の特徴量を抽出します。
inputs = inputs.reshape(-1, 1, 4, 4)
c1 = conv1(inputs)
c1 = torch.nn.functional.relu(c1)
p1 = pool(c1)
c2 = conv2(p1)
c2 = torch.nn.functional.relu(c2)
p2 = pool(c2)
inputs2fc = p2.reshape(-1, 2 * 2 * 2)
inputs2fc = inputs2fc.detach() # 勾配計算はしない
#print(inputs2fc)
#for idx, item in enumerate(zip(inputs2fc, labels)):
# print(f'idx: {idx}, item: {item[0].data}, label: {item[1]}')
これらのデータを使って学習を行う全結合型のニューラルネットワークは次のようにします。
class Net(torch.nn.Module):
def __init__(self):
super().__init__()
self.fc1 = torch.nn.Linear(8, 10)
self.fc2 = torch.nn.Linear(10, 1)
def forward(self, x):
x = self.fc1(x)
x = torch.sigmoid(x)
x = self.fc2(x)
x = torch.sigmoid(x)
return x
このニューラルネットワークモデルへの入力は、既に見た通り8個だったので、入力層のノード数は8としています(隠れ層のノード数「10」は筆者が適当に決めたものです)。ここでは横線か縦線かを判断するので(2クラス分類)、出力層のノード数は1つになっています。この値が0.5より小さければ、0(横線)、0.5以上なら縦線(1)という判断をするように正解ラベルを設定してあります(インスタンス変数fc2の出力を活性化関数であるtorch.sigmoid関数に渡すことで、出力が0〜1の範囲に収まるようにしている点に注意)。
学習を行うコードは次の通りです。
import torch.optim as optim
net = Net()
criterion = torch.nn.BCELoss()
optimizer = optim.SGD(net.parameters(), lr=0.03)
EPOCHS = 10000
for epoch in range(1, EPOCHS + 1):
optimizer.zero_grad()
outputs = net(inputs2fc)
loss = criterion(outputs.squeeze(), labels)
loss.backward()
optimizer.step()
if epoch % 500 == 0:
print(f'#{epoch}, loss: {loss.data}')
print('Finished')
predicted = (outputs.reshape(1, -1) + 0.5).int()
(predicted == labels).sum().item()
実行結果を以下に示します。
それなりに学習できたようなので、このニューラルネットワークモデルに、先ほど作成した4つの特徴量を入力してみましょう。
print(pooled2)
result = net(pooled2)
print(result)
4つのデータは順に横線/縦線/よれた横線/左下がりの直線を表すものでした。これらがうまく判断できたでしょうか。
1つ目と3つ目の推測値は横線を表す0に極めて近いものになっていますし、2つ目の推測値は縦線を表す1に極めて近いものになっているので、どうやらこのニューラルネットワークモデルはうまいこと推測を行えているようです。最後のデータについては、0にも1にも近くない中間の値となっているので、左下がりの直線をどう判断すればよいか難しいことを表しているといえます。
最後に、今までに見てきた畳み込み、プーリング、全結合を行うニューラルネットワーククラスをひとまとめにしたクラスも示しておきましょう。興味のある方は、上で示した学習を行うコードを少し改変して、学習を行い、畳み込み層の重みがどのようになるかを確認してみてください(公開しているノートブックにはそれらのコードも含めてあります)。
class Net2(torch.nn.Module):
def __init__(self):
super().__init__()
self.conv1 = torch.nn.Conv2d(1, 2, 3, padding=True, bias=False)
self.pool = torch.nn.MaxPool2d(2, padding=1)
self.conv2 = torch.nn.Conv2d(2, 2, 3, padding=True, bias=False)
self.fc1 = torch.nn.Linear(8, 10)
self.fc2 = torch.nn.Linear(10, 1)
def forward(self, x):
x = self.conv1(x)
x = torch.relu(x)
x = self.pool(x)
x = self.conv2(x)
x = torch.relu(x)
x = self.pool(x)
x = x.reshape(-1, 2 * 2 * 2)
x = self.fc1(x)
x = torch.sigmoid(x)
x = self.fc2(x)
x = torch.sigmoid(x)
return x
今回は前回に説明した内容を、実際にコードを動かしながら確認してみました。次回は学習に関連する事項について少し見ていくことにします。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 実行結果
実行結果 実行結果
実行結果 実行結果
実行結果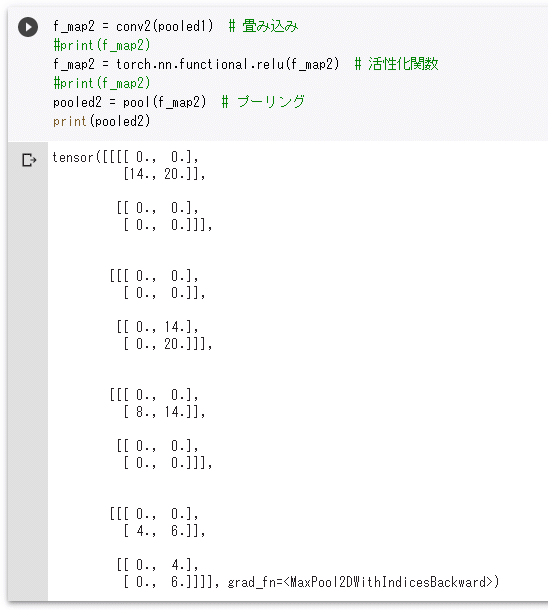 実行結果
実行結果 実行結果
実行結果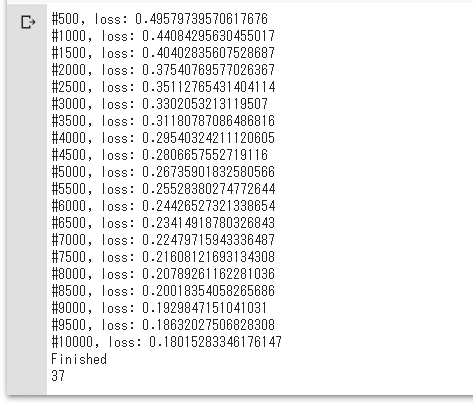 実行結果
実行結果 実行結果
実行結果



