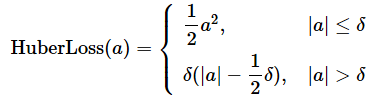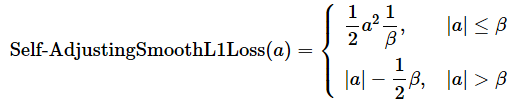［損失関数］Huber損失（Huber Loss）／Smooth L1 Lossとは？：AI・機械学習の用語辞典

用語「Huber損失」について説明。損失関数の一つで、各データに対する「予測値と正解値の差（＝誤差）」が、指定したパラメーター値の範囲内の場合は二乗値を使った計算、範囲外の場合は絶対値を使った計算の結果値のこと、もしくはその計算結果の総和をデータ数で割った値（＝平均値）を表す。

» 2021年08月04日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

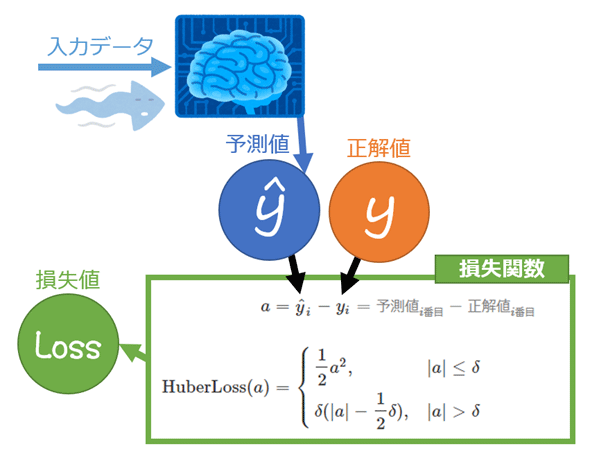
　統計学／機械学習におけるHuber損失（Huber Loss：フーバー損失、英語読みならヒューバー・ロス）とは、調整可能なパラメーターδ（デルタ）を例えば1.0とした場合、各データに対して「予測値と正解値の差（＝誤差、残差）」が0.0～1.0（δ）の範囲では「誤差の二乗値に0.5（＝1/2）を掛けた値」を計算し、1.0（δ）より大きい（外れ値になる可能性が高い）範囲では「誤差の絶対値から0.5を引いた値」を計算する関数のこと（図1）、もしくはその計算結果の総和をデータ数で割った値（＝平均値）を出力する関数を指す。なお誤差は、「予測値－正解値」ではなく「正解値－予測値」でもよい。

図1　「Huber損失」のイメージ

定義と数式

　計算式をシンプルにするために、各データに対する「予測値と正解値の差」（以下、誤差）の計算値をaにまとめた。このaを次の式で用いている。また、δ（デルタ）は調整可能なパラメーターで、正の実数を指定できる。δは外れ値に応じて指定した方がよいが、デフォルトでは1.0が指定されることが多い。

　Huber損失の計算式は2つに分かれており、これをグラフにするなら、上の式が二次関数の曲線を描き、下の式が一次関数の直線を描くことになる点に着目してほしい。つまり誤差の絶対値が、δ以下のときは曲線、δより大きいときは直線のグラフとなる（図2の青色の線）。2つに分ける意味は、後述の用途と特徴で説明する。

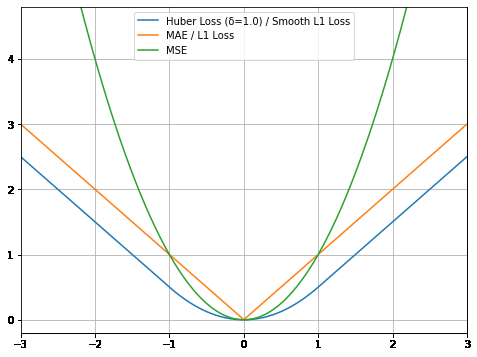図1　「Huber損失」のグラフ（横軸：入力値＝誤差、縦軸：出力値＝損失）
比較しやすいようにグラフ内に3種類の線を描いた。
・青色の線： Huber損失＝下記2つの弱点を克服した
・オレンジ色の線： MAE（平均絶対誤差）／L1損失＝0地点で「微分不可能」で、0に近い場所でも勾配が大きいという弱点がある
・緑色の線： MSE（平均二乗誤差）＝外れ値に敏感という弱点がある（例えば横軸の入力値が3のとき、縦軸の出力値は9と非常に大きな値となりグラフからはみ出している）

Smooth L1 Lossとは

　Huber損失に密接に関係する損失関数にSmooth L1 Loss（滑らかなL1損失）がある。Smooth L1 Lossは、Huber損失の計算式にあるδに1.0を指定した場合と同じ計算式となる。Smooth L1 Lossは、例えばモデルアーキテクチャ「Fast R-CNN」の損失関数として使われるなど、勾配爆発を防ぐ目的で特に物体検出でよく使われている。

　δに1.0を指定するだけなので、Smooth L1 Lossは通常のHuber損失の関数で実現できる。だが、PyTorchのAPIではHuber損失とは別にSmoothL1Lossクラスが用意されている。このクラスは、Self-Adjusting Smooth L1 Loss（自己調整する滑らかなL1損失、この損失関数の論文）の形式で実装されており、β（ベータ）という調整可能なパラメーターが追加されている点が異なる。Self-Adjusting Smooth L1 Lossの計算式は以下の通りで（※Huber損失と何が違うかが分かりやすいように書いた）、βに1.0を指定した場合は通常のSmooth L1 Lossと同じ計算式になる。

用途と特徴

　Huber損失は主に、回帰問題における最適化のための損失関数として使われる。

　なお、分類問題用の損失関数として「Huber損失の修正バージョン」が使われることもたまにある。例えばscikit-learnライブラリには、回帰向けのSGDRegressor(loss='huber')クラスに対応する形で、分類向けのSGDClassifier(loss='modified_huber')クラスも用意されている。このクラスのインスタンス化で引数に指定する'modified_huber'が「Huber損失の修正バージョン（Modified Huber Loss）」を意味する（※計算式などの詳細は本稿では割愛する。この損失関数の論文）。

　回帰問題の損失関数といえば、まずはMAE（平均絶対誤差）／L1損失（L1 Loss）やMSE（平均二乗誤差）が挙げられるが、MAEには誤差が0の地点で「微分不可能」という欠点や、0に近い場所でも勾配が大きいままという欠点があり、MSEは外れ値の影響を受けやすいという欠点がある（※イメージしづらい場合は前掲の図1を再確認してほしい）。これらの欠点を克服するためには、損失関数の入力値と出力値のグラフにおいて、0の地点で微分可能にして、かつ0に近くなるほど緩やかな勾配にするために入力値（＝誤差）が0に近い範囲ではMSEと同様に滑らか（＝スムーズな）曲線を描き、外れ値があるような外側に続く範囲はMAEと同様に直線を描くような損失関数の数式にすればよい。これを実現したのが、Huber損失の数式（前述）である。

　つまりMSEやMAEの欠点が原因の問題（特に勾配爆発）が発生する場面で、それらの代わりにHuber損失が使えるというわけである。

　強化学習でも学習を安定させるためによく使われており、筆者の経験では例えば強化学習を行うAWS DeepRacerで、MSEの代わりにHuber損失を選択できた。他には、TensorFlow／Keras公式の「CartPole（台車でポールのバランスを取るゲーム）」強化学習チュートリアルなどでHuber損失が使われている。

　ちなみにHuber損失は、統計学者のPeter J. Huber（ペーター・J・フーバー）氏によるロバスト統計学（ロバスト＝頑健な、つまり外れ値に対して強い統計学）の論文「Robust Estimation of a Location Parameter」（1964年）で発表された。