［損失関数／評価関数］平均絶対誤差（MAE：Mean Absolute Error）／L1損失（L1 Loss）とは？：AI・機械学習の用語辞典

用語「平均絶対誤差」について説明。損失関数／評価関数の一つで、各データに対して「予測値と正解値の差（＝誤差）」の絶対値を計算し、その総和をデータ数で割った値（＝平均値）を表す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

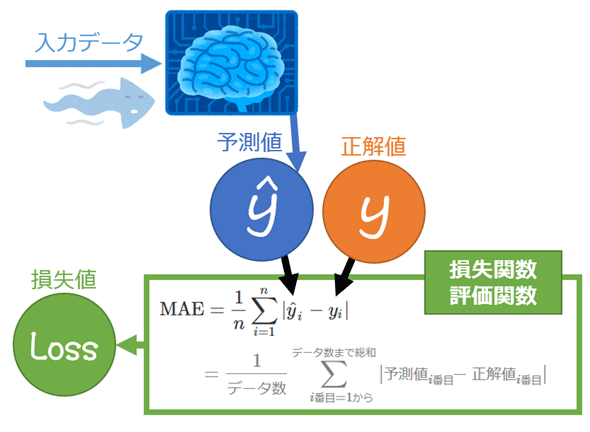
　統計学／機械学習における平均絶対誤差（MAE：Mean Absolute Error）とは、各データに対して「予測値と正解値の差（＝誤差）」の絶対値を計算し、その総和をデータ数で割った値（＝平均値）を出力する関数である。（図1）。なお誤差は、「予測値−正解値」ではなく「正解値−予測値」でもよい（ただし両者では微分時の結果の＋1／−1が逆になる）。

図1　「平均絶対誤差」のイメージ

定義と数式

　上記の式から1/nを外すと（＝総和だけで平均しない場合）、L1ノルム（マンハッタン距離）の式と同じになる。このことからMAEは、L1損失（L1 Loss）やL1ノルム損失（L1-norm Loss）とも呼ばれる。

用途と特徴

　MAEは主に、回帰問題における出力層の評価関数として用いられる。また、損失関数として使われることもある。

　MAEよりもMSE（平均二乗誤差）やRMSE（MSEの平方根）の方が有名であるが、MSE／RMSEは誤差を二乗するため元の数値と単位が変わってしまうので（例えば元の数値「1」を2乗すると→出力結果は「1」、10の2乗→100、100の2乗→10,000と大きく単位が変化するので）、人間にとって評価値／損失値をシンプルに理解するのが難しいという問題がある。一方、MAEであれば、絶対値しか計算しないので元の数値から単位が変化せず、人間にとってシンプルで理解しやすいという利点がある。「評価関数や損失関数の出力値」が人間にとって解釈しやすいことを重要視するならば、MSE／RMSEではなくこのMAEを使えばよいだろう。またMAEは、MSE／RMSEよりも外れ値の影響を受けにくいという利点もある（これも単位が変わらないことの恩恵）。

　MAEの欠点として、絶対値は数学計算で条件分岐が発生して数式が2つ（予測値＞正解値の場合の微分係数は1、予測値＜正解値の場合は-1）に分かれてしまう問題があり、特にその分岐地点（予測値＝正解値の場合）では数学的に「微分不可能」になるという問題がある。このため、損失関数として原則的にはやや使いづらいといえる。また、MSE／RMSEのように、誤差が大きくてもそれほど過大には評価してくれないので（＝先ほどの外れ値の影響を受けにくい利点の裏返し）、より評価しづらい指標ともいえるだろう。

API

　主要ライブラリでは、次のクラス／関数で定義されている。

• scikit-learn： mean_absolute_error関数
• TensorFlow（2.x）／Keras： MeanAbsoluteErrorクラスやmean_absolute_error()関数、また（compile()メソッドの引数metricsで）'mean_absolute_error'や'MAE'など
• PyTorch： L1Lossクラスやl1_loss()関数

「AI・機械学習の用語辞典」