[損失関数/評価関数]平均二乗誤差(MSE:Mean Squared Error)/RMSE(MSEの平方根)とは?:AI・機械学習の用語辞典
用語「平均二乗誤差」について説明。損失関数/評価関数の一つで、各データに対して「予測値と正解値の差(=誤差)」の二乗値を計算し、その総和をデータ数で割った値(=平均値)を表す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説「MSE」
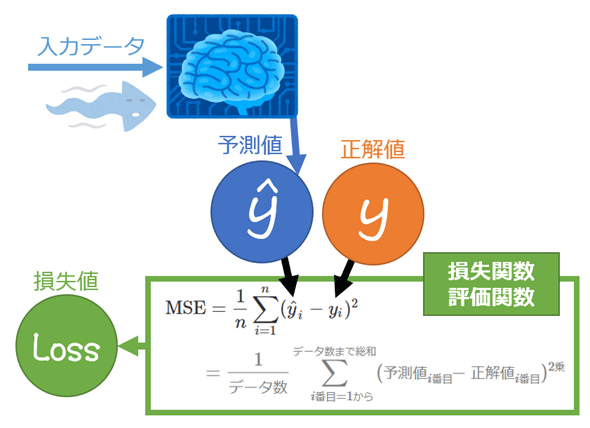
統計学/機械学習における平均二乗誤差(MSE:Mean Squared Error)とは、各データに対して「予測値と正解値の差(=誤差)」の二乗値を計算し、その総和をデータ数で割った値(=平均値)を出力する関数である。(図1)。なお誤差は、「予測値−正解値」ではなく「正解値−予測値」でもよい。
定義と数式
上記の式から1/nを外すと(=総和だけで平均しない場合)、「二乗したL2ノルム(ユークリッド距離)」(=平方根√しないL2ノルム)の式と同じになる。二乗したL2ノルムや、それに1/2を掛けたものは、L2損失(L2 Loss)とも呼ばれる。
用途
MSEは、最も一般的な損失関数として使われるだけでなく、主に回帰問題における出力層の評価関数としても用いられる。いずれの関数から出力される値も、0に近いほどより良い。
MSEや後述するRMSEは、誤差を二乗する。そのため、誤差が大きいほど過大に評価する、つまり間違いをより重要視するという特徴がある。MSE/RMSEは、評価がしやすい指標といえるだろう。
その利点の裏返しとして、外れ値に過敏に反応してしまうことにもなるので、損失関数として利用する場合は外れ値にも過剰適合(=過学習)してしまいやすいという問題がある。
また、MSEは誤差を二乗することで単位が変わってしまうので(例えば元の数値「1」を2乗すると→出力結果は「1」、10の2乗→100、100の2乗→10,000と単位が変化するので)、人間にとって単純には理解しづらいことが欠点として挙げられる。この単位問題を回避する方法としては、絶対値を使う方法(MAE:平均絶対誤差)や、ルート(√)を使って二乗した単位を元の単位に戻す方法(後述のRMSE:Root MSE)が考えられる。
API
主要ライブラリでMSEは、次のクラス/関数で定義されている。
- scikit-learn: mean_squared_error関数
- TensorFlow(2.x)/Keras: MeanSquaredErrorクラスやmean_squared_error()関数、また(compile()メソッドの引数metricsで)'mean_squared_error'や'MSE'など
- PyTorch: MSELossクラスやmse_loss()関数
用語解説「RMSE」
RMSE(Root MSE:MSEの平方根)とは、名前の通り、MSEの結果に対するルート(√)を求めることである。MSEで二乗した単位が元に戻るので、MSEよりも人間が理解しやすい指標だといえる。
定義と数式
API
主要ライブラリでRMSEは、次のクラス/関数で定義されている。
- scikit-learn: mean_squared_error関数の引数squaredにFalseを指定
- TensorFlow(2.x)/Keras: RootMeanSquaredErrorクラス
- PyTorch: MSELossクラスやmse_loss()関数の出力結果からtorch.sqrt()関数などを使って平方根を計算
ここを更新しました(2023年11月6日)
PyTorchのmse_loss()関数のリンク切れを修正しました。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ