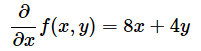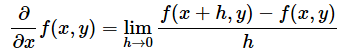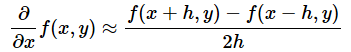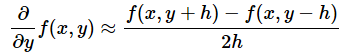微分法の数値計算をプログラミングしてみよう:数学×Pythonプログラミング入門(4/4 ページ)
練習問題
それでは、練習問題に取り組み、ここまで見てきた数値計算の方法を確実に身に付けましょう。練習問題についても、プログラムの作成例と実行例を動画で紹介しています。解答例のコードについては、1行ずつ細かく解説することはしていませんが、大きな流れをつかむためにぜひ視聴してみてください。
動画4 微分法をプログラミングする練習問題
(1)勾配降下法で関数の最小値を求める
以下の関数はxの二乗の項の係数が正なので、下に凸なグラフとなり、最小値が存在します。
この関数の値を最小にするxの値(これをaとします)を勾配降下法で求めてみてください。勾配降下法では、aをまずランダムに決め、学習率と呼ばれる小さな値を決めておきます。ここでは学習率を0.001としましょう。続いて以下の繰り返しを行います。
- 微分係数f'(a)を求める
- 微分係数が正であれば、aの値はより小さい方にあるはずなので、aの値から|学習率 × 微分係数|を引いて、新しいaとする
- 逆に、微分係数が負であれば、aの値はより大きい方にあるはずなので、aの値に|学習率 × 微分係数|を足して、新しいaとする
学習率 × 微分係数が正であれば絶対値を引き、負であれば絶対値を足すということは、結局のところ、学習率 × 微分係数を引くだけでいいということになりますね(負の値を引くということは足すということなので)。
このようにして、新しいaを次々と求め、微分係数が十分0に近づけば(あるいは、f(a)の値がほとんど変化しなくなったら)、そのときのaを答えとするわけです。
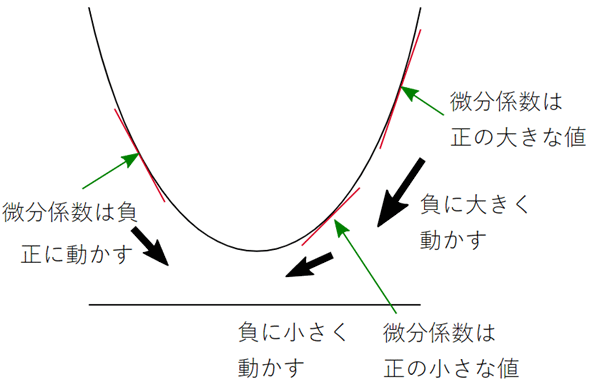 図8 勾配降下法を使って二次式を最小にするxの値を求める
図8 勾配降下法を使って二次式を最小にするxの値を求めるランダムに決めた値を初期値として、学習率×微分係数を引いて次の値を求める。この操作を繰り返し、微分係数が0に近づけば(接線の傾きが水平になるので)、二次式の値が最小になることが分かる。
なお、勾配降下法については、「[AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する」の最後の方でも紹介してします。
もちろん、導関数が解析的に求められるのであれば、解析的に求めた導関数を使って微分係数を求めればいいので、わざわざ数値計算を行う求める必要はありません。上の例も簡単に微分でき、導関数はf'(a)=6a−24となります。さらに、f'(a)=0と置いて方程式を解けば、答え(a=4)が求められます。また、勾配降下法では、大きな学習率を設定すると、収束しないことがあるので注意が必要です。
しかし、ここでは練習のために、微分の定義に従って微分係数の近似値を求め、その値を使って勾配降下法を試してみることにしましょう。答えが4に近い値になれば正解です。
(ヒント) 回数を指定した繰り返し処理ではないので、while文を使うといいでしょう。微分係数が十分0に近づくまで、あるいは、直前のf(a)と、その時点でのf(a)との差が0に近づくまでの繰り返しになりますが、後者では、最小値に近づくにつれ、差がきわめて小さくなるので、十分に収束する前に繰り返しが終わることがあります。
(2)2変数の微分方程式をルンゲ・クッタ法で解く
以下の微分方程式を、x=0, y=1を初期条件としてルンゲ・クッタ法で数値計算し、グラフを描いてみてください。刻み値hは0.001とします。
なお、この微分方程式を解析的に解くと、
となります。x=0, y=1という初期条件で求めた特殊解を使ってグラフを作成し、2つのグラフを重ねて描きましょう。以下のような結果になるはずです。
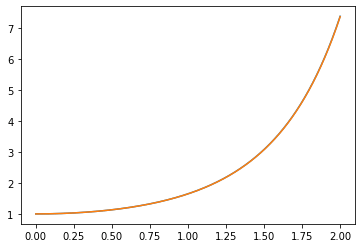 図9 2変数の微分方程式をルンゲ・クッタ法で数値計算して描いたグラフ
図9 2変数の微分方程式をルンゲ・クッタ法で数値計算して描いたグラフやはり、解析的に解いた関数のグラフと重なるので、ブルーのグラフが背後に隠れて見えなくなっていれば正解(ブルーのグラフがオレンジのグラフとかけ離れて見える場合はどこかに間違いがある)。
(ヒント) 簡単です。ノーヒントでやってみましょう。
(3)偏微分の数値計算を行い、平面のグラフを描く
最初に説明した微分法の数値計算と同じ考え方で偏微分もできます。
例えば、関数f(x,y)をxで偏微分する場合、導関数は、
と表されます。この定義を参考に、中心差分近似を使って以下の関数をxで偏微分し、そのグラフを描いてみてください。
結果は以下のようになります。3Dグラフとして描画する必要があるので、この連載の第4回の練習問題(2)「多変数関数で表された曲面のグラフを描く」を参考にして作成してみてください。
(ヒント) 以下のコードの穴埋めでやってみましょう
import numpy as np
import matplotlib.pyplot as plt
def partial(f, x, y, h):
# ここに、中心差分近似によって求めた偏微分係数を返すコードを書く
def func(x, y):
# ここに、関数f(x, y)の定義を書く
h = 0.01
xrange = np.arange(0, 2, h)
yrange = np.arange(0, 2, h)
x, y = np.meshgrid(xrange, yrange) # xとyの交点の座標を全て返す
z = # ここに、xとyの座標を指定して、全ての偏微分係数を求めるコードを書く
plt.figure(figsize=[8, 6])
ax = plt.subplot(projection='3d')
ax.plot_surface(x, y, z, cmap='YlOrRd')
曲面(平面)のグラフを描くためのコードについては、既に書かれているものをそのまま使えばよい。NumPyのmeshgrid関数はxとyの交点の座標を全て返す。それらの値を使って偏微分の数値計算を行い、zの値を求めるとよい。
練習問題の解答例
以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではりません。
(1)勾配降下法で関数の最小値を求める
ここでは、微分係数が十分0に近づくまで繰り返す例(リスト16)と、元の関数の値がほとんど変化しなくなるまで繰り返す例(リスト17)の両方を作ってみました。関数funcを最小にするaの値だけでなく、そのときの微分係数と収束までの回数も求めています。
import random
def func(x):
return 3*x**2 - 24*x + 331
def derivative(f, x, h):
return (f(x+h) - f(x)) / h
h = 0.001
rate = 0.001 # 学習率
random.seed(0) # 毎回同じ結果を得るために乱数の種を設定
a = random.random() # 初期値
coef = 1 # 微分係数(とりあえず1から始める)
count = 0 # 収束までの回数を数えてみる
while abs(coef) > 0.001:
a -= rate * coef # aの値を更新する
coef = derivative(func, a, h)
count += 1
print(a, coef, count) # aとそのときの微分係数、収束までの回数
学習率はrate、関数funcの微分係数はcoef。rateとcoefの積をaから引いて、coefの絶対値が十分0に近くなるまで繰り返す。毎回同じ結果が得られるように、乱数の種(初期値)を決めておいた。コードを実行すると、aが3.9993337892878147となり、解析的に求めた4に近くなっていることが分かる。また、coefは-0.0009972642374123097、countは1638となる。1638回の繰り返しで収束したことが分かる。
import random
def func(x):
return 3*x**2 - 24*x + 331
def derivative(f, x, h):
return (f(x+h) - f(x)) / h
h = 0.001
rate = 0.001 # 学習率
random.seed(0) # 毎回同じ結果を得るために乱数の種を設定
a = random.random() # 初期値
coef = derivative(func, a, h) # 最初の微分係数
prev = func(a) # 最初のfunc(a)の値
diff = 1 # 直前の値との差。1から始めることにする
count = 0 # 収束までの回数を数えてみる
while abs(diff) > 1e-8:
a -= rate * coef # aの値を更新する
coef = derivative(func, a, h)
curr = func(a) # 今回のfunc(a)の値
diff = prev - curr # 直前のfunc(a)との差
prev = curr # 今回の値を直前の値にしておく
count += 1
print(a, coef, count) # aとそのときの微分係数、収束までの回数
繰り返しの条件が異なるだけで、学習率×微分係数を使ってaを更新するという基本的な考え方は同じ。while文では、収束条件として1e-8(=0.00000001)というかなり小さい値を指定してあるが、これはリスト16と繰り返し数を同じぐらいするためあえて小さくしたため。このコードを実行すると、aが3.9991700306827553、coefが-0.001979815920094552、countが1523となる。
(2)2変数の微分方程式をルンゲ・クッタ法で解く
微分方程式の定義を変えるだけです。簡単すぎましたね。微分方程式の一般解が、
なので、初期条件がx=0, y=1であれば、C=1となり、特殊解は、
となります。
import numpy as np
import matplotlib.pyplot as plt
def dy(x, y):
return x * y # ここを変えるだけ
def RungeKutta(x, y, h):
k1 = dy(x, y)
k2 = dy(x+h/2, y+h*k1/2)
k3 = dy(x+h/2, y+h*k2/2)
k4 = dy(x+h, y+h*k3)
ky = y + h*(k1+2*k2+2*k3+k4)/6
return ky
y = [1]
h = 0.001
for x in np.arange(h, 2, h):
y.append(RungeKutta(x, y[-1], h))
x = np.arange(0, 2, h)
plt.plot(x, y)
plt.plot(x, np.exp(x**22)) # 解析的に解いたグラフも描画
plt.show()
微分方程式を表す関数dyの定義を変えただけ。微分方程式を解析的に解いた場合の式も、特殊解に合わせてnp.exp(x**2/2)に変えただけ。
(3)偏微分の数値計算を行い、平面のグラフを描く
f(x,y)をxで偏微分する場合、導関数は、
でした。これを中心差分法で近似するなら、
という式を使えばいいいですね。ちなみに、yで偏微分するなら
という式を使います。
import numpy as np
import matplotlib.pyplot as plt
def partial(f, x, y, h):
return (f(x+h, y) - f(x-h, y)) / (2*h)
def func(x, y):
return 4*x**2 + 4*x*y + 2*y**2 + 5
h = 0.01
xrange = np.arange(0, 2, h)
yrange = np.arange(0, 2, h)
x, y = np.meshgrid(xrange, yrange)
z = partial(func, x, y, h)
plt.figure(figsize=[8, 6])
ax = plt.subplot(projection='3d')
ax.plot_surface(x, y, z, cmap='YlOrRd')
関数funcの内容をreturn 8*x + 4*yとし、zへの代入文をz=func(x, y)に変更すれば、解析的に偏微分を行って求めた式(8x+4y)を使ってグラフが描けるので、見比べてみるとよい。
今回は、微分に関する数値計算について見てきましたが、定義通りに微分する方法に加え、オイラー法やルンゲ・クッタ法を使って微分方程式を解く方法も学びました。次回は、積分法の数値計算について見ていこうと思います。台形公式やシンプソンの公式による基本的な数値計算の方法に加え、モンテカルロ法を使った近似値の計算などのプログラミングについて見ていきます。
Copyright© Digital Advantage Corp. All Rights Reserved.

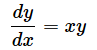
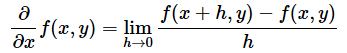
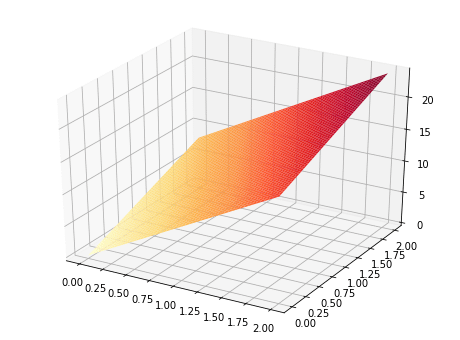 図10 偏微分の数値計算によって描かれた平面のグラフ
図10 偏微分の数値計算によって描かれた平面のグラフ