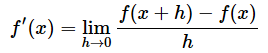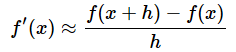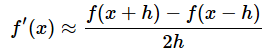微分法の数値計算をプログラミングしてみよう：数学×Pythonプログラミング入門（1/4 ページ）
微分法に関する数値計算のプログラミング方法を見ていく。最初に定義通りに計算する方法を、次に微分方程式を簡単に数値計算する方法を紹介。最後に、ルンゲ・クッタ法と呼ばれる精度のよい近似方法を見る。
この記事は会員限定です。会員登録（無料）すると全てご覧いただけます。
前回は、データの可視化をテーマに、さまざまなグラフの描画を行いました。今回は「変化」を捉えるために使われる微分法について、数値計算のプログラミング方法を見ていきます。
まず、微分の定義を思い出しながら、プログラムとして表現する方法を紹介します。次に、微分方程式の数値計算を行います。関連事項として、ルンゲ・クッタ法による微分方程式の解法についても紹介します。今回はPythonの文法やライブラリに関しての新出事項は特にありませんが、いくつかのアルゴリズムを通して、プログラミングの力を高めていきます。
今回の練習問題としては、勾配降下法により最小値を求めるプログラム、2変数の微分方程式をルンゲ・クッタ法で解くプログラム、偏微分の数値計算を行うプログラムの3つを取り上げます。
微分方程式やルンゲ・クッタ法は中学・高校の数学のレベルを少し超えますが、数値計算は簡単な四則演算だけでできてしまうので、微分の考え方さえ分かっていれば、容易に理解できるはずです。
連載：
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI／機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
羽山博筆者紹介： IT系ライター、大学教員（非常勤）。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。
目標1： 微分の数値計算を行って導関数をグラフ化しよう
例えば、以下のような関数があったとします。この関数そのものには特に意味はありませんが、答えが簡単に分かり、検算もしやすいので、例として取り上げることにしました。
この関数を微分すると、以下のような関数（導関数）が得られます。……というより、そもそも微分係数や導関数を求めることが微分するということでしたね。
このように、数式を変形して微分などの計算を行うことを解析的に解くと言います。しかし、今回の目標1は、解析的に解くことではありません。（1）式そのものから、xの値を少しずつ変えていきながら、それに対するf'(x)の近似値を次々と求めることを目標とします。そのような計算の方法を数値計算と呼びます。xとf'(x)の値が求められれば、図1のようなグラフが描けます。
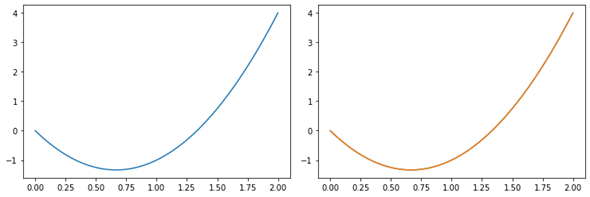図1 f(x) ＝ x3 − 2x2 ＋ 1の導関数のグラフx＝0〜2まで、0.001刻みでグラフを描いた例。
左側のブルーの線が数値計算によって求めた近似値のグラフ。
右側のグラフは、数値計算によるグラフ（ブルーの線）に重ねて、解析的に求めた関数f'(x) ＝ 3x2−4xのグラフ（オレンジ色の線）を描いたもの。ほとんど一致するので、背後に表示されているブルーの線が隠されて見えなくなっている。
というわけで、図1の左側のグラフを描いてみましょう。もちろん、解析的に求めた（2）式をそのまま使ってグラフを描くのは反則です。導関数の定義を基に、（1）式を使って数値計算を行い、グラフを描くことにします。今回のサンプルプログラムについても、紹介動画を用意してあります。1行1行解説しているわけではなく、作成から実行までの流れを紹介したものなので、全体像と実行結果を確認するのにご利用ください。
動画1 二次関数の数値計算によって求めた近似値でグラフを描く方法
1. 導関数の定義をコードとして表す
実は、導関数の定義さえ覚えていれば、（1）式から（2）式への変形ができなくても、コードを書くことができます。関数f(x)に対する導関数f'(x)の定義については、数学の教科書に必ず掲載されているので、見慣れたものだと思います。以下の通りでしたね。
hの値は限りなく0に近づきますが、0ではありません。そこで、hをごく小さな値であるものとして、ほぼ等しいという意味の記号≈を使って表すなら、
と表せます。≈は「ニアリーイコール」などと読みます。上の数式をPythonの関数を使ったコードとして表すとリスト1のようになります。
def derivative(f, x, h):
return (f(x+h) - f(x)) / h
関数derivativeは導関数の定義をそのままコードとして表しただけ。引数として渡すfは導関数を求める元の関数。
ここでは、（1）式の関数（以下に再掲）を微分するので、こちらもPythonのコードで関数として定義しておきましょう（リスト2）。
コードは以下の通りです。簡単ですね。
def func(x):
return x**3 - 2*x**2 + 1
こちらも関数の定義をそのままコードとして表しただけ。これを関数derivativeに渡せば、xの値に対する微分係数の近似値が求められる。
この関数funcが関数derivativeに渡されることになります。xの値を0〜2（未満）まで0.001刻みで変えながら、関数derivativeを呼び出せば、それぞれのxの値に対する微分係数が求められます。求めた微分係数を順にプロットすれば、導関数のグラフになるというわけです。……といっても、微分の考え方を忘れていると、コードは書けても意味が分からないので、念のため図解しておきましょう（図2）。これについては、動画も用意しておきました。導関数がどのようにプロットされるのかを確認するためにご参照ください。
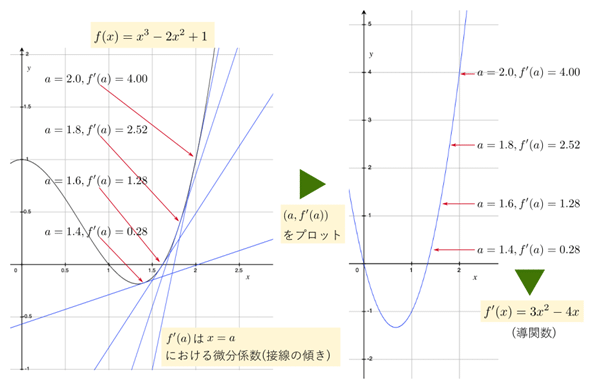図2 微分係数を関数として表したものが導関数左側の図が元の関数のグラフ。x＝aにおける接線の傾き、つまり微分係数f'(a)を順に求めていき、右側の図のように、aとf'(a)の値をプロットしていけば、関数のグラフが出来上がることが分かる。図には一部の値しか示していないが、「くまなく」プロットすれば連続したグラフとなる。このようにして得られた関数が導関数。
動画2 微分係数を順にプロットして導関数のグラフを描画する流れ
というわけで、xの値を0〜2（未満）まで0.001刻みで変えながら、関数derivativeを呼び出し、次々とグラフ化するデータを作っていきます。リスト3のような繰り返し処理で書いてみましょう（より簡潔に書く方法は後で紹介します）。
import numpy as np
import matplotlib.pyplot as plt
h = 0.001
xrange = np.arange(0, 2, h)
data = []
for x in xrange:
data.append(derivative(func, x, h))
plt.plot(xrange, data)
plt.show()
最初に空のリストdataを用意しておき、xの値を0から2未満までhずつ変えながら、関数derivativeを呼び出し、微分係数を求めてリストdataに追加していく。matplotlib.pyplotモジュールのplot関数を使って、xrange（xの範囲）を横軸の値、dataを縦軸の値として折れ線グラフを描く。
実行結果は、目標のところで見た通りです。
ところで、ここでは、f(x＋h)−f(x)のように、f(x)の「次の値」からf(x)を引いた値を使って近似値を求めています。そのため、この方法は前進差分近似と呼ばれます。結果はあくまで近似値なので、例えば、x＝0のとき、f'(x)の近似値は-0.001999となります。一方、解析的に答えを求めると0になります。少し誤差が大きくなっていますね。そこで、精度のよい近似として、中心差分近似と呼ばれる以下のような方法も使われます。
ちなみに、中心差分近似では、x＝0のとき、f'(x)の近似値は0.000001となります*1。
*1 hの値をもっともっと小さくして、細かく刻んでいけばよりよい近似値が得られると思われるかもしれません。しかし、hの値をあまりにも小さくしすぎると、極めて小さな値で割り算を行うため、誤差が拡大し、かえってよい近似値が得られません（それ以前に、hの値が小さすぎると、計算時間がかかりすぎて使い物になりません。なお、誤差についてはまた回を改めて説明したいと思います）。
では、もう少し簡潔にコードを書く方法も紹介しておきましょう。リスト4のように、リスト内包表記を使うと、短い行数で同じことができます。
import numpy as np
import matplotlib.pyplot as plt
h = 0.001
xrange = np.arange(0, 2, h)
data = [derivative(func, x, h) for x in xrange]
plt.plot(xrange, data)
plt.show()
リスト内包表記を使って、関数derivativeの値を全て求めたリストを作成し、dataに代入する。
さらに、xrangeはNumPyの配列（ndarray）なので、ブロードキャスト機能を使った書き方にすれば、より簡潔に書けます（リスト5）。
import numpy as np
import matplotlib.pyplot as plt
h = 0.001
xrange = np.arange(0, 2, h)
data = derivative(func, xrange, h)
plt.plot(xrange, data)
plt.plot(xrange, 3*xrange**2 - 4*xrange) # 解析的に求めた例も追加した
plt.show()
NumPyのブロードキャスト機能を使えば、xrangeの全ての値について、関数derivativeを呼び出した結果が配列として求められる。その配列をdataに代入する。ここでは、dataの形式はリストではなくndarrayとなる。なお、リスト5には、解析的に求めた導関数を使ってグラフを描くコードも追加しておいた。
微分の数値計算を行う方法は、（1）式のようなxの多項式だけでなく、三角関数や対数関数などであっても全く同じです。高校時代に(sinθ)' ＝ cosθなどの、微分の公式を覚えるのに苦労した記憶がある人も多いと思いますが、そういった公式を使う必要はありません*2。
*2 というわけで、高校の数学で学んだような微分の公式は、ここでは一切不要ですが、検算のために解析的に導関数を求めたい方は、「［AI・機械学習の数学］微分法の基本を身につけて「変化」を見極めよう」を参照していただくといいでしょう。特に多項式の微分については、その記事の目標【その4】に記してある通りです。つまり、
のとき、
となることさえ覚えておけば、微分の計算ができます。
実際のところ、解析的に微分できるのであれば、このような方法で数値計算する必要はないのですが、次に取り組む微分方程式などでは、解析的に解を得るのが難しい場合があります。数値計算はそのような場合に便利です。
Copyright© Digital Advantage Corp. All Rights Reserved.
ITmediaはアイティメディア株式会社の登録商標です。