加重平均とは？　算術平均との違い、使い分け：AI・機械学習の用語辞典

用語「加重平均」について説明。算術平均がデータの合計値をデータ数で割った値なのに対し、加重平均は重み付けしたデータの合計値を全ての重みの合計値で割った値を表す。各データが異なる重要度を持つ場合に適した平均の計算方法だ。

» 2023年10月16日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

　最も一般的に使われる「平均」とは、全ての数値を足して合計し、それを数値の総数で割ることである。これは、数学／統計学／機械学習において「算術平均」と呼ばれる。平均には他にも、「加重平均」や「幾何平均」「調和平均」「トリム平均」「移動平均」などがある。本稿ではこれらのうち加重平均について解説する。なお算術平均については、「平均値（Mean）／中央値（Median）／最頻値（Mode）とは？」で説明しているので併せて参照してほしい。

　数学／統計学／機械学習における加重平均（Weighted Mean）とは、データの各数値に重み付けした上で全て足した合計値を、全ての重みの合計値で割ることである。

図1　加重平均のイメージ

　以下では「算術平均と何が違うのか」が分かるように、算術平均と加重平均の計算方法と数学公式を紹介し、最後に使い分け指針をまとめる。計算方法の説明は冒頭の説明の繰り返しになるが、公式の意味を分かりやすくするために記述したので、ご了承いただきたい。

算術平均

　算術平均（Arithmetic Mean）値とは、データの各数値（x_iは、数値₁, 数値₂, ..., 数値_nのいずれかの数値）を全て足した合計値をデータ数（n）で割った値のことである。算術平均は相加平均とも呼ばれる。数学の公式は以下のようになる。

　算術平均は、最も一般的な「平均」の計算方法で、通常はこれを使えばよい。例えば月ごとの平均気温を求めたり、英語の試験の平均点を求めたりするのに使える。

加重平均

　加重平均（Weighted Mean）値とは、データの各数値（x_iは、数値₁, 数値₂, ..., 数値_nのいずれかの数値）に、それぞれに対応する重み（w_iは、重み₁, 重み₂, ..., 重み_nのいずれかの数値）を掛けた（＝各数値に重み付けした）上で全て足した合計値を、全ての重みの和で割った値のことである。数学の公式は以下のようになる（nはデータ数）。

　この式は、厳密には加重算術平均（Weighted Arithmetic Mean）の式となる。詳細は割愛するが、加重中央値や、加重幾何平均、加重調和平均など、“加重”と名前が付く計算方法が他にもあり、それらとの違いを明示する場合は「加重算術平均」と呼ばれることが多い。

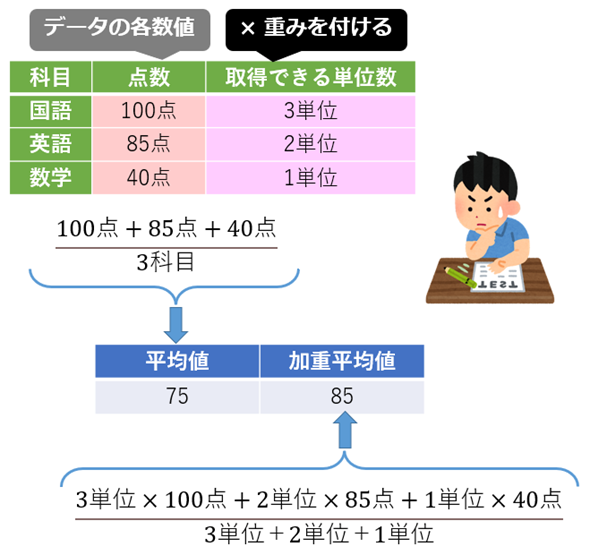
　加重平均は、数値ごとに重要度や影響度が異なる場合に、算術平均の代わりに用いるとよい。例えば国英数の3科目の試験があり、国語は3単位、英語は2単位、数学は1単位が取得できる場合、科目ごとに点数の重要度が異なることになり、国語の点数が一番重要である。このケースでは、単位数に基づく各科目の点数の重要度を考慮した平均値を求めるために、算術平均の代わりに加重平均を採用することが考えられる。実際に採用したとして、以下の数値例で加重平均値を計算してみよう。

国語: 成績 100、取得できる単位数 3
英語: 成績 85、取得できる単位数 2
数学: 成績 40、取得できる単位数 1

　算術平均値の計算では、合計225点（＝100＋85＋40）を3科目で割るので、平均75点が求まる。

　加重平均値の計算では、合計510点（＝3×100＋2×85＋1×40）を6単位（＝3＋2＋1）で割るので、平均85点が求まる。

　この加重平均の計算例では、国語をより重視し、数学をより軽視する平均点が求まった。つまり、より実態を反映した平均値が求まったと言えるだろう。