平均値（Mean）／中央値（Median）／最頻値（Mode）とは？：AI・機械学習の用語辞典

用語「平均値」「中央値」「最頻値」について説明。平均値はデータの合計値をデータ数で割った値、中央値はデータを順番に並べた際に中央に位置する値、最頻値は最も頻繁に出現する値を表す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

平均値

　数学／統計学／機械学習における平均（mean、average）値とは、データを全て足した合計値をデータ数で割った値のことである。なお、平均値にも種類が幾つかあるが（算術平均／加重平均／幾何平均／調和平均など）、ここでいう平均値は最も一般的な算術平均（arithmetic mean）を指す。算術平均は相加平均とも呼ばれる。

代表値

　平均値は、数学や統計学ではデータを代表する値を意味する代表値（central tendency）に分類される。代表値には、主に下記の3種類がある。

• 平均値
• 中央値
• 最頻値

図1　代表値「平均値／中央値／最頻値」のイメージ

中央値

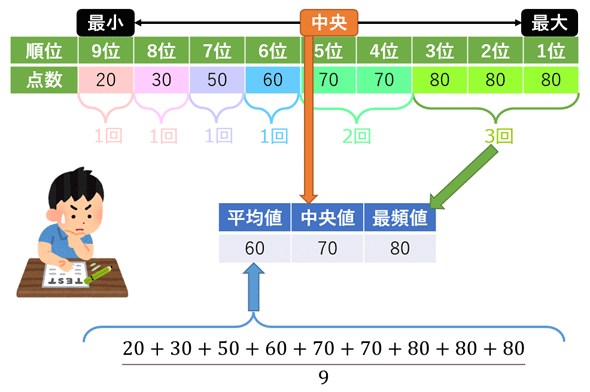
　中央（median）値とは、データを昇順もしくは降順に並べた上で真ん中の順位に位置する値のことである。図1の例では、1〜9位の真ん中の順位である5位が中央値となる。データ数が奇数の場合は真ん中の順位が存在するが、偶数の場合は真ん中が2つになってしまう。例えば1〜10位にすると、真ん中は5位と6位になる。このような場合には、5位と6位の平均値を中央値とするのが一般的だ。

最頻値

　最頻（most frequent）値／モード（mode）値とは、最も頻繁に出現する値である。図1の例では、80という値が3個であり最も出現回数が多いので最頻値となる。なお、もし最も頻出する値が複数ある場合、それら全てが最頻値となる。

代表値の違いと使い分け指針

　通常は、平均値が最も使い勝手がよく、これを使えばよい。

　しかし、極端な外れ値があり、それに平均値が引っ張られる場合は、平均値の代わりに中央値を使った方がよいこともある。例えば図1は20点や30点を取った人に平均点が引っ張られている。20点や30点の影響を受けないようにしたい場合には、中央値を使えばよい。ただし、中央値はデータ全体の変化を追ったり、データ間を比較したりするのには向いていない。例えば数学のテストの点を、前月から今月でどれくらい伸びたかを見たい場合や、A高校とB高校で比較したい場合には、やはり平均値を使った方がよい。

　データのヒストグラムが正規分布のようにきれいな山型の分布ではない場合は、平均値や中央値の代わりに最頻値を使った方がよいこともある。最頻値は、「どの値が出やすいか」という傾向を見るのに最適な代表値であり、外れ値を含めて値の大小に鈍感である。例えば30点に10人、80点に11人、他の0〜100点の10点おきに全て1人ずつというデータの場合、平均値は54点で、中央値は55点になるが、最頻値は80点となる。

　このような特徴から、（あまりないかもしれないが）データ上での多数決を優先したいようなケースでは、最頻値が役立つと考えられる。例えば満足度評価を9段階で取得した場合、平均値や中央値にすると結果が真ん中の「どちらでもない（5）」に寄りがちになる可能性がある。「好き（8や9）」と「嫌い（1や2）」に2分化されているデータならば、平均して「どちらでもない」という結果になるのを避けて、多数決で「好きが多いか」「嫌いが多いか」をはっきりさせたいのではないだろうか。こういったケースでは、平均値とともに最頻値も併せて見るとよいだろう（ヒストグラムを作ってデータの度数分布を見てもよい）。

　筆者なりに使い分けの一例を書いてみたが、あらゆるケースは想定できない点をご了承いただきたい。ケース・バイ・ケースで状況に合わせて、「平均値のままでよいか？　中央値や最頻値の方がデータの意味を捉えやすいのではないか？」と、適切な代表値を考えることが大切である。

「AI・機械学習の用語辞典」

ここを更新しました（2023年11月6日）

加重平均／幾何平均／調和平均、それぞれの用語解説ページへのリンクを張りました。算術平均が「相加平均」とも呼ばれる点を追記しました。