[解決!Python]エラトステネスのふるいで素数を求めるには:解決!Python
指定した整数までの素数を、エラトステネスのふるいと呼ばれる手法で求める方法を見たあと、それを関数として定義し、その関数を使って、指定した値が素数かどうかを判定する関数を定義してみよう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
# リストを使ったバージョン
target = 30
limit = int(target ** 0.5) + 1
primes = [False] * 2 + [True] * (target - 1) # primes[n]がTrueならnは素数
for n in range(2, limit):
if primes[n]:
primes[n * 2::n] = [False] * len(primes[n * 2::n])
result = [i for i in range(target + 1) if primes[i]]
print(result) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
# 辞書を使ったバージョン
target = 30
limit = int(target ** 0.5) + 1
primes = {n: True for n in range(2, target + 1)} # primes[n]がTrueならnは素数
for n in range(2, limit):
if primes[n]:
primes |= {i: False for i in range(n * 2, target + 1, n)}
result = [n for n in primes if primes[n]]
print(result) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
# 関数にする
def eratosthenes(target):
limit = int(target ** 0.5) + 1
primes = [False] * 2 + [True] * (target - 1)
for n in range(2, limit):
if primes[n]:
primes[n * 2::n] = [False] * len(primes[n * 2::n])
result = [n for n in range(target + 1) if primes[n]]
return result
target = 30
prime_nums = eratosthenes(target)
print(prime_nums) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
# ある数が素数かどうかを判定する関数
def is_prime(n):
if n <= 1:
return False
primes = eratosthenes(n)
if n in primes:
return True
return False
target = 29
result = is_prime(target)
print(result) # True
エラトステネスのふるいによる素数の取得
エラトステネスのふるいとは、古代ギリシアの数学者であるエラトステネスが考案したとされる、2から整数Nまでの範囲にある素数を求めるやり方のこと。簡単にまとめると「2からNまでの表(ふるい)を作成する。そして、2は素数なので、その倍数を表から消していく。次に3は素数なので、その倍数を表から消していく。……といった手順で素数の倍数を表から消していき、最後に残ったものが2からNまでの範囲にある素数となる」というものだ。
例えば、29までの素数を求めるとしよう(作表の都合で中途半端な数になっている。これは以下で紹介するPythonのリストを使ったコードでは、0始まりのインデックスを用いて素数かどうかを判定するのが簡単だからだ)。初期状態の表は次のようになる。
0と1は素数ではない(素数とは1と自分自身のみを約数とする数である)ので、表では最初から素数ではないとして、×を付けている。2は素数なので○を付けている。
次にこの表(ふるい)から2の倍数を削除していく(実際のコードではリストや辞書の値を素数ならTrue、素数でなければFalseとしていく)。この結果が以下だ。
次の素数である3についても同様だ。この結果は次のようになる。
4はすでにふるいに掛けられているので、次に5を見ると、これも素数なのでその倍数をふるいに掛けていく。
このような処理をしていき、最終的には以下が素数として得られた。
ふるいに掛ける整数の上限
エラトステネスのふるいでは、ある整数Nまでの素数を求める際に、その平方根√Nまでの整数を試せばよいとされている。これはなぜだろう。
ある整数Nが素数ではなく、約数aとbを持っている(整数Nが合成数である)とすると、「N=a×b」と表現できる。このとき、「a ≦ b」と仮定する。そして、この不等式の両辺にaを乗算すると、「a×a ≦ a×b」つまり「a2 ≦ N」となる。ここで両者の平方根を取ると「a ≦ √N」となる。また、先の不等式にbを乗算すると、同様な計算の結果、「√N ≦ b」となる。つまり、整数Nが約数を持つときには一方の約数は√N以下となり、もう一方の約数は√N以上となる。
整数Nが約数を持つときには一方は必ず√N以下の値となるので、ふるいに掛けるときに試す値は√N以下の整数でよいということだ。例えば、30までの素数を求めるのであれば、√30$は約5.48なので、2、3、4、5についてふるいに掛けていけばよい(上で見た図の通り)。
Pythonで実装する
上記のアルゴリズムをPythonのリストを使って実装すると次のようになる。ここでは29ではなく30までの素数を求めるコードになっている。
target = 30
limit = int(target ** 0.5) + 1
primes = [False] * 2 + [True] * (target - 1) # primes[n]がTrueならnは素数
for n in range(2, limit):
if primes[n]:
primes[n * 2::n] = [False] * len(primes[n * 2::n])
result = [i for i in range(target + 1) if primes[i]]
print(result) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
リストではインデックスが検討対象の値、対応する値がTrueならそのインデックス値は素数であり、Falseなら素数ではないものとしている。リストのインデックスは0始まりなので、ふるいとして使っているリストprimesの先頭にある2つの要素の値はFalseとなるように、それ以降の要素の値はTrueとなるように初期化している(「primes = [False] * 2 + [True] * (target - 1)」)。
変数limitには上のコラムで説明した理由から、探索対象の値(ここではtarget)の平方根を整数化した値(に1を足したもの。range関数で2からその値までを取り扱えるようにするため)が代入されている。そして、2からその値までの範囲でリストprimesを使って素数かどうかを判定して、素数の倍数をふるいに掛けている。「primes[n * 2::n] = [False] * len(primes[n * 2::n])」というのは、素数の倍数となる要素の値をFalseにしている。n=2を例に取ると「primes[2 * 2::2]」は「primes[4::2]」でありインデックス4の要素から1個飛ばしの要素(4→6→8→……)というスライスである。これにそのスライスの要素数と同じ個数の「[False, False, False, ……]」を代入している。
最後の「result = [i for i in range(target + 1) if primes[i]]」はリストprimesでその値がTrueとなっているインデックスのみを集めた、つまり素数からなるリストを作成するものだ。
同様なことは辞書を使っても行える。整数をキーとして、そのキーが素数かどうかを示すブーリアン値を値とする要素を辞書に格納しているので、人によってはこちらの方が意味を取りやすいかもしれない。
target = 30
limit = int(target ** 0.5) + 1
primes = {n: True for n in range(2, target + 1)} # primes[n]がTrueならnは素数
for n in range(2, limit):
if primes[n]:
primes |= {i: False for i in range(n * 2, target + 1, n)}
result = [n for n in primes if primes[n]]
print(result) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
やっていることはリストを使ったバージョンと同様だ。「primes |= {i: False for i in range(n * 2, target + 1, n)}」は辞書内包表記を使って、{素数の倍数: False}という要素を集めた辞書を作成して、「|=」演算子により、作成した辞書で元の辞書を更新するコードだ。
これらのうち、リストを使ったバージョンを関数にしたものが以下だ。
def eratosthenes(target):
limit = int(target ** 0.5) + 1
primes = [False] * 2 + [True] * (target - 1)
for n in range(2, limit):
if primes[n]:
primes[n * 2::n] = [False] * len(primes[n * 2::n])
result = [n for n in range(target + 1) if primes[n]]
return result
target = 30
prime_nums = eratosthenes(target)
print(prime_nums) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
このeratosthenes関数については特に説明の必要はないだろう。これは指定した値までの素数を求める関数だが、特定の値が素数かどうかを調べたいのであれば、以下のような関数を定義すればよい。
def is_prime(n):
if n <= 1:
return False
primes = eratosthenes(n)
if n in primes:
return True
return False
target = 29
result = is_prime(target)
print(result) # True
is_prime関数は与えられた数までの素数をeratosthenes関数で求めた上で、その値が素数リストに含まれているかどうかを調べて、TrueまたはFalseを返すものだ。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 初期状態の表(ふるい)
初期状態の表(ふるい)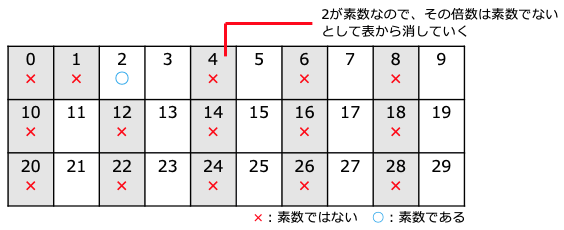 2の倍数をふるいに掛けたところ
2の倍数をふるいに掛けたところ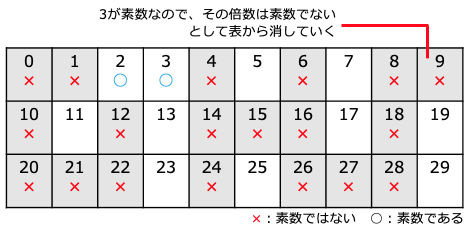 3の倍数をふるいに掛けたところ
3の倍数をふるいに掛けたところ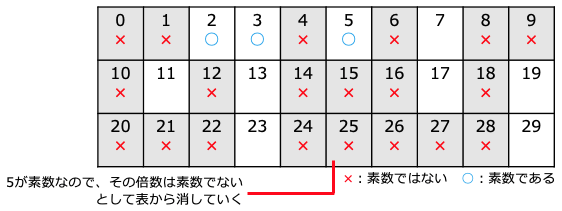 5の倍数をふるいに掛けたところ
5の倍数をふるいに掛けたところ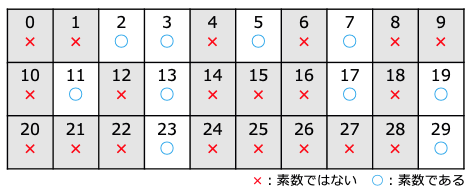 得られた素数
得られた素数



