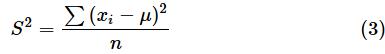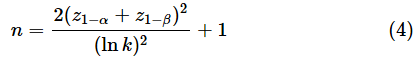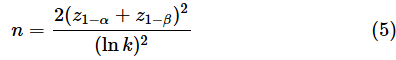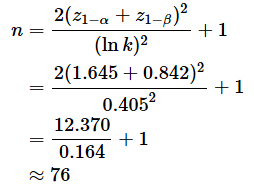【Excelで学ぶデータ分析】動画視聴時間のバラツキが、ある値より大きいか調べたい（分散の検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第4回。今回は、正規分布する母集団の分散がある値よりも大きいかどうかを検定する方法について解説します。

» 2025年10月09日 05時00分公開

連載：

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第4回です。前回は、正規分布する2つの母集団の平均に差があるかどうかを検定する方法を解説しました。今回は正規分布する母集団の分散（母分散）が、ある値よりも小さいか（あるいは大きいか／異なるか）を検定する方法を見ていきます。

母分散の検定についての基本的な考え方

　前々回と前回は、母平均の検定や母平均の差の検定を行いました。今回は母集団のバラツキ、つまり母分散に注目し、そのための検定を見ていきます。

　今回のテーマを、単刀直入に帰無仮説として表すと、以下のようなものになります（帰無仮説の意味については、こちらで既に解説しました。要するに無に帰したい＝棄却したい仮説のことですね）。母集団の分散をσ₁²とし、「ある値」をσ₀²とすると、

H₀：母集団の分散が「ある値」と等しい（σ₁²＝σ₀²）

となります。帰無仮説を棄却したときに採用したい対立仮説H₁としては、以下の3つのいずれかが考えられます。

H₁：母集団の分散が「ある値」よりも大きい（σ₁² > σ₀²）
H₁：母集団の分散が「ある値」よりも小さい（σ₁² < σ₀²）
H₁：母集団の分散が「ある値」とは異なる（σ₁² ≠ σ₀²）

　今回は、対立仮説がσ₁² > σ₀²である例を取り上げます。具体的なイメージを見ておきましょう。

　10歳代～70歳代のインターネット動画視聴者を対象に、視聴時間（分単位）のアンケートを採ったところ、標本平均が193.5、不偏分散が5554.66（不偏標準偏差は74.53）であったものとします。過去の経験から分散は4200（標準偏差は64.81）であることが分かっているとき、母分散が大きくなったといえるでしょうか。母集団の視聴時間は正規分布するものとします（正規分布が仮定できない場合の検定方法は後述します）。ただし、データは架空のものです。

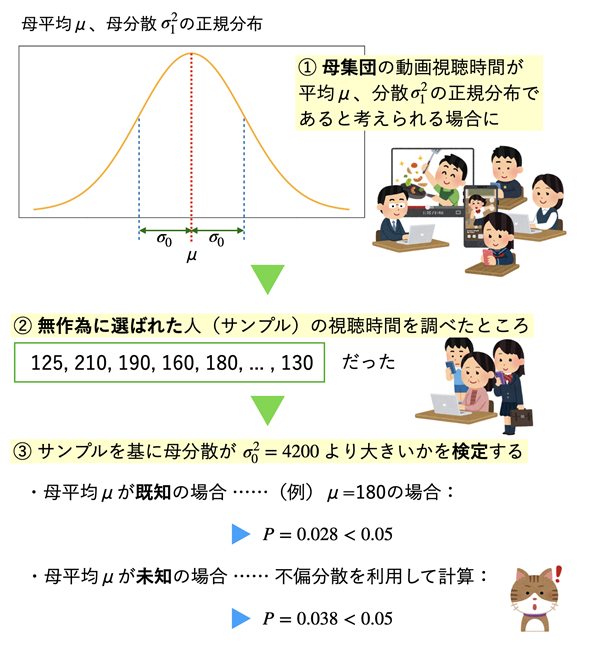図1　動画の視聴時間のバラツキは、ある値よりも大きくなったのか？
母分散の検定を行うためには、大前提として、母集団の視聴時間が正規分布していることが必要。これまでの経験から動画視聴時間の分散が4200であることが分かっているものとして、その値よりも母分散が大きくなったかどうかを検定する。

　NHK放送文化研究所による『放送研究と調査』2021年8月号の『新しい生活の兆しとテレビ視聴の今』で紹介されている国民生活時間調査2020の結果では、日曜日のインターネット動画視聴について、視聴したことのない人も含めた全体の平均時間は32分、標準偏差は86分となっています。その中で、一度でも視聴したことのある人の平均視聴時間は91分（1時間31分）となっています（標準偏差は掲載されていません）。上のデータはその値を参考にしていますが、架空のものです。なお、元の資料には平日・土曜、男女別、年齢層別の値も掲載されています。

　母分散の検定については、母平均が既知の場合と未知の場合とで計算方法が異なります。これまでの連載では「既知の場合→未知の場合」の順に説明してきましたが、Excelの関数を使うのであれば、母平均が未知の場合の方が簡単にできるので、そちらから先に見ていきます。

母分散の検定を行ってみよう～母平均が未知の場合

　普通は、母平均が既知の場合よりも未知である場合の方が一般的です。その場合、検定統計量Tとして、

の値を求めます。s²は不偏分散なので、VAR.S関数で求められます。このようにして求めたTの値を基に、自由度n－1のカイ二乗分布の右側確率を求めます。その計算はCHISQ.DIST.RT関数で簡単にできます。

　こちらからダウンロードしたExcelファイルを開いて試してみてください。［母分散の検定 (母平均が未知)］ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

図2　母分散の検定（母平均が未知の場合）
セルD4の標本平均は既にAVERAGE関数で求められており、セルD5のサンプルサイズnもCOUNT関数で求められている。セルD6にVAR.S関数を入力して、（1）式のs²の値を求める。σ₀²の値はセルD9に入力されているので、これらの値を基にセルD10で検定統計量Tを求め、セルD11でCHIDSQ.DIST.RT関数でP値を求める。

　結果は、P＝0.038<0.05なので5％有意となり、対立仮説の「母分散は4200より大きい」を採用します。この結果をどのように評価するかは、母分散の検定（母平均が既知の場合）の後で説明します。

　ここでは、（1）式によって求めた検定統計量を基に、CHISQ.DIST.RT関数で右側確率を求めましたが、対立仮説H₁によって計算の方法が異なります。以下に箇条書きでまとめておきます。

H₁がσ₁² > σ₀²の場合： CHISQ.DIST.RT関数を使って右側確率を求める。
H₁がσ₁² < σ₀²の場合： CHISQ.DIST関数を使って左側確率を求める。
- ただし、CHISQ.DIST関数は確率密度関数の値と累積分布確率の値のどちらを求めるかを、第3引数で指定する必要がある（TRUEなら累積分布確率、FALSEなら確率密度関数となります）。
H₁がσ₁² ≠ σ₀²の場合： CHISQ.DIST関数の結果とCHISQ.DIST.RT関数の結果の小さい方を2倍して両側確率を求める。

　続いて、母分散の検定（母平均が既知の場合）を行ってみましょう。

母分散の検定を行ってみよう～母平均が既知の場合

　母平均が既知の場合には、検定統計量Tは以下の式で求めます。

　ただし、

とします。S²はVAR.P関数で求められる標本分散の値とは異なることに注意が必要です。各データから母平均を引き、それを2乗した値の総合計をデータの個数で割る、ということです。

　（2）式で求めたTの値を基に、自由度nのカイ二乗分布の右側確率を求めます。図3は、母平均が180であると分かっている場合の計算例です。［母分散の検定 (母平均が既知)］ワークシートを表示して図3のように入力してください。

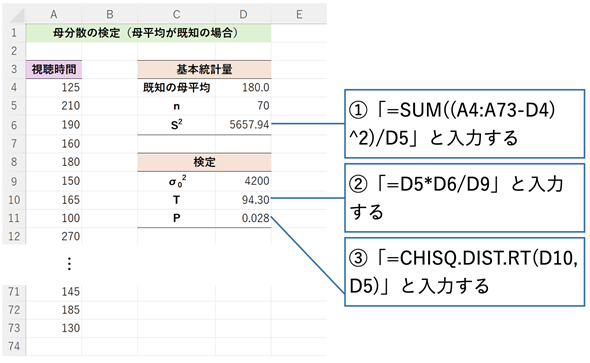図3　母分散の検定（母平均が既知の場合）
セルD4の値はAVERAGE関数を使って求めた標本平均ではなく、既に分かっている母平均の値が入力されていることに注意。また、セルD5のサンプルサイズnはCOUNT関数を使って求められている。（3）式のS²の値は、セルD6に「=SUM((A4:A73-D4)^2)/D5」と入力して求める（古いバージョンのExcelでスピル機能が使えない場合については後述する）。セルD9がσ₀²の値。これらの値を基に、セルD10で（2）式により検定統計量Tを求める。セルD11のCHIDSQ.DIST.RT関数に検定統計量Tとnの値を指定すればP値が求められる。

　セルD6に入力する数式は配列数式を使っているので、スピル機能が使えないExcelバージョンの場合は、数式の入力終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す必要があります。なお、Googleスプレッドシートでは、セルD6には「=ARRAYFORMULA(SUM((A4:A73-D4)^2)/D5)」と入力します。

　結果は、P＝0.028<0.05なので5％有意となり、対立仮説の「母分散は4200より大きい」を採用します。この例とは異なる対立仮説での計算方法については、母平均が未知の場合と同じ考え方です。

母分散の検定結果をどう解釈するか

　母分散の検定の結果、帰無仮説が棄却され、対立仮説のσ₁² > σ₀²が採用されることになりました。つまり、「母分散σ₁²は、σ₀²＝4200よりも大きい」と考えてよさそうだ、というわけです。

　分散が大きくなったということは、視聴時間のバラツキが大きくなったということですね。つまり、平均から離れた値が多くなった、ということです。平均的な視聴時間の人が多いのではなく、短い視聴時間の人も長い視聴時間の人も多い、ということです。このことから、よく視聴する人は視聴時間が長くなり、あまり視聴しない人は視聴時間が短くなったことが示唆されます。

　イメージが湧くように、簡単なデータで不偏分散を計算し、ヒストグラムを作成した例を図4に示します（［分散の比較（作成例）］ワークシートで確認できます。古いバージョンのExcelでは表示できませんが、表示するための入力方法は後述します）。平均的な視聴時間の人が多いということは正規分布に近いということですね。一方、短い視聴時間の人も長い視聴時間の人も多いということは一様分布に近いということです。それぞれのバラツキについて、セルE4とF4に表示されている不偏分散を比較してみてください。乱数を使っているので、Excelの場合は［F9］キーを押して再計算（Googleスプレッドシートの場合は［F5］キーでリロード）を実行するたびに値やグラフの表示が変わります。

　計算に使った式の一覧は図4の後に箇条書きで記しておきます（グラフの作成手順については省略します）。

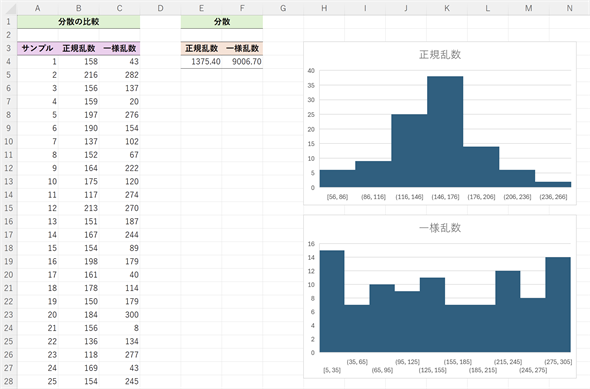図4　正規分布と一様分布の分散とヒストグラム
正規乱数により、平均150、標準偏差40の正規分布のサンプルを作成し、一様乱数により、100から300までの一様分布のサンプルを作成。正規分布の場合は平均の近くに値が集まっている。一様分布の場合は平均から離れた値も多い。セルE4とセルF4がそれぞれの不偏分散。

　入力されている数式は以下の通りです。データは4～103行目までの100件です。RANDARRAY関数は複数の乱数を一気に作成するために使っています。

セルB4に「=INT(NORM.INV(RANDARRAY(100),150,40))」と入力する
- Excel 2019以前ではRANDARRAY関数が使えないので、セルB4に「=NORM.INV(RAND(), 150, 40)」と入力し、セルB103までコピーする
- Googleスプレッドシートでは、セルB4に「=ARRAYFORMULA(INT(NORMINV(RANDARRAY(100),150,40)))」と入力する
セルC4に「=RANDARRAY(100,1,0,300,TRUE)」と入力する
- Excel 2019以前ではセルC4に「=RANDBETWEEN(0, 300)」と入力し、セルC103までコピーする
- Googleスプレッドシートでは、セルC4に「=ARRAYFORMULA(INT(RANDARRAY(100)*300))」と入力する
セルE4に「=VAR.S(B4:B103)」と入力する
セルF4に「=VAR.S(C4:C103)」と入力する（セルE4をセルF4にコピーしてもよい）

コラム　可視化と検定結果の解釈に関する落とし穴

　今回の例を基に、実践的な場面で行き過ぎた解釈をしてしまう落とし穴を少し紹介します。最初にお話ししたように、今回のサンプルは10歳代～70歳代のインターネット動画視聴者を対象としたものです。また、各年代のサンプルサイズは同じです。

　動画視聴時間のバラツキが既に知られていた値よりも大きくなったということは、これまでより、幅広い年代でインターネット動画が視聴されるようになった、と考える人もいるかもしれません。しかし、その解釈は正しくありません。

　実は、「10歳代～70歳代」「各年代のサンプルサイズが同じ」と書いたのはちょっとしたひっかけです。「正規分布する」とも言っているので、なんとなく、図5に示すような20歳代～30歳代の山のあるグラフを想像してしまいそうです。しかし、今回のサンプルでは、年齢に関するデータはどこにもありません。

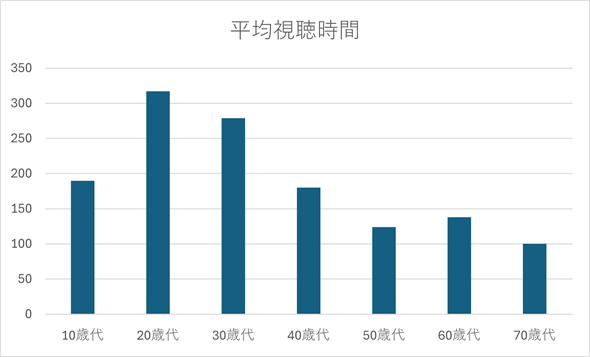図5　年齢を横軸に取った平均視聴時間のグラフ（今回のサンプルからは作れない）
このような形のデータであることを想像してしまうが、今回のサンプルからはこのようなグラフは作成できないし、棒グラフで分布は可視化できない。分布を可視化するためにはヒストグラムを作る必要がある。

　今回のサンプルは、あくまでも視聴時間だけのデータです。つまり、図5に示すような分布ではないということです。そもそも、図5は縦軸が度数であるヒストグラムではなく、縦軸が平均視聴時間である棒グラフです。分布はヒストグラムによって可視化できますが、棒グラフは分布の可視化ではなく、カテゴリごとの値の大小を比較するものです。図5は各サンプルの視聴時間を年代ごとに集計して平均を求めたものをプロットしたものになっています。

　ちなみに、幅広い年代でインターネット動画が視聴されるようになると、どの年齢層の人も平均値に近づくので、かえって分散は小さくなります。グラフのそれぞれの棒が同じぐらいの高さになるので、ばらつきが大きくなったように見えるかもしれませんが、どの年代でも平均値に近い値になる、ということです。くどいようですが、棒グラフとヒストグラムは異なるものです。

　なお、縦軸が「平均視聴時間が150分以上の人数」であれば、ヒストグラムが描けます。その場合は、年齢によって、長時間の視聴者がどう分布するのかが分かります。サンプルファイルの［年代別の視聴時間］ワークシートに図5の例と、「平均視聴時間が150分以上の人数」をヒストグラムにしたものを含めてあるので、参照してみてください。ただし、違いが理解できればいいので、表やグラフの作成方法については解説しません（また、それらを作成するための架空の元データは［年代別 (作業データ)］ワークシートに記録してあります）。

　ところで、年代別の違いを見たいときにはどうすればいいの？　という疑問が生じると思います。母分散の検定に使ったサンプルには年齢の値が含まれていないので、これ以上の分析はできませんが、年齢別にサンプルを収集したのであれば、分散分析により、年齢による視聴時間に違いがあるかどうかを調べることができます。分散分析については、この連載の最終回で紹介する予定です。

母集団が正規分布であると仮定できない場合は？～ブートストラップ法

　母平均に関しては、中心極限定理により、サンプルサイズが大きければ、母平均の検定や母平均の差の検定ができました。しかし、母分散の検定には、中心極限定理は適用できません。そのため、サンプルサイズが大きくても、母集団が正規分布に従っていない場合には上記の検定ができません。では、どうすればいいでしょう。

　実は、この連載の区間推定編でその答えを紹介しています。こちらで解説したブートストラップ法を使います。手順は以下の通りです。

サンプルを基に、重複ありでリサンプリングを行い、不偏分散を求める
その不偏分散をリストに追加する（以上を何度も繰り返す）
リストの値のうち、σ₀²以下の個数が全体の個数の何％かを求める

　多数の繰り返しをExcelで行うのは面倒なので、Pythonで作成したプログラムを紹介しておきます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行してみてください。

# ブートストラップ法
import numpy as np

# 既知の値
sigma0_sq = 4200

# データ
data = np.array([125, 210, 190, 160, 180, 150, 165, 100, 270, 240,
                 215, 200, 105, 125, 240, 370, 160, 175, 120, 260,
                 180, 80, 185, 310, 90, 180, 135, 135, 220, 200,
                 160, 45, 200, 250, 240, 355, 140, 280, 210, 180,
                 285, 160, 250, 310, 185, 120, 300, 115, 150, 180,
                 250, 85, 70, 140, 221, 170, 220, 165, 85, 360,
                 170, 150, 180, 320, 330, 300, 280, 145, 185, 130])

n_bst = 10000 # ブートストラップの回数
bst_var = [] # サンプルの不偏分散を記録するリスト

np.random.seed(0) # 乱数の種を固定

# データからn=70個のサンプルを重複ありで、n_bst回取り出す
n = data.size
for _ in range(n_bst):
    sample = np.random.choice(data, size=n, replace=True)
    # 不偏分散を計算して、リストに追加する
    bst_var.append(np.var(sample, ddof=1))

# 既知の値以下になる確率を求める
bst_var = np.array(bst_var)
# 以下の()の中はTRUEかFALSEの配列となる。
# TRUEは1、FALSEは0と見なされるので、平均を求めるとTRUEの確率が求められる。
print(np.mean(bst_var <= sigma0_sq)) # 実行すると0.0599という結果が得られる

ブートストラップ法のPythonコード例

　上のコードを実行すると、0.0599となります。母集団の正規性が仮定できない場合は、帰無仮説が棄却できません（だからといって、乱数の種を変えたり、繰り返し数を変えたりして有意差を出そうとするのは邪道です）。

母分散の検定での適切なサンプルサイズは？

　最後に、適切なサンプルサイズの求め方を見ておきます。有意水準α＝0.05、検出力1－β＝0.8とし、効果量としては分散の比k＝σ₁²/σ₀²を使います。ここでは、理屈抜きに式だけを示します。

　母分散が未知の場合は以下の式を使います。

　母分散が既知の場合は以下の式を使います。

　z_1－αは標準正規分布の1－α点の値です（両側検定の場合はz_1－α/2とします）。また、lnは自然対数です。母分散が未知の場合、正確にはカイ二乗分布を利用する必要がありますが、一般的には、標準正規分布を使った近似で見積もることができます（余裕を持って＋1～＋2しておくといいでしょう）。具体例で計算してみましょう。

　例えば、σ₀²＝4200とし、母分散σ₁²を6300と見積もったものとします。このとき、z_1－α＝1.645, z_1－β＝0.842, k＝6300/4200＝1.5, ln k＝0.405なので、

となります。余裕を見てn＝77としましょう。サンプルファイルの［サンプルサイズ (母平均未知)］ワークシートにこの計算例を含めてあります。また、［サンプルサイズ (母平均既知)］には（5）式での計算例を含めてあります。

　Excelでは、カイ二乗分布を利用してサンプルサイズを求めるのが面倒なので、Pythonを使って求めた例を、ブートストラップ法と同じファイルに含めてあります。2つ目のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行してみてください。n＝74という結果が表示されます。

　今回は、母分散の検定方法を解説しました。しかし、母分散がある値と等しいかどうかを検定する場面は、実際にはあまりないかもしれません。むしろ、独立した2群について、それらの母分散が等しいかどうかを検定する場合の方がよくあります。

　というわけで、次回は母分散の比の検定に取り組みます。一般に、等分散性の検定と呼ばれたり、F検定と呼ばれたりすることもよくあります。名前からしてF分布を利用することが想像できますね。次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。

複数の乱数を作成するために使った関数

RANDARRAY関数：乱数の配列を作成する

形式

RANDARRAY(行数, 列数, 最小値, 最大値, 値の種類)

引数

行数： 作成する乱数の行数。省略すると1と見なされる。
列数： 作成する乱数の列数。省略すると1と見なされる。
最小値： 作成する乱数の最小値。省略すると0と見なされる。
最大値： 作成する乱数の最大値。省略すると1と見なされる。
値の種類： 整数の乱数を作成する場合はTRUEを、小数点以下のある乱数を作成する場合はFALSEを指定する。省略するとFALSEと見なされる。