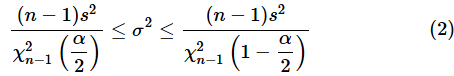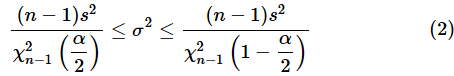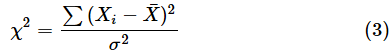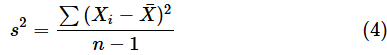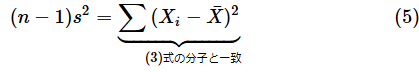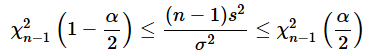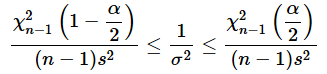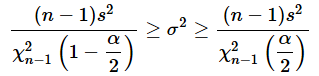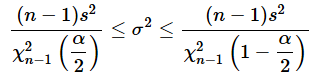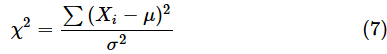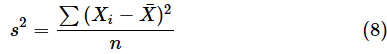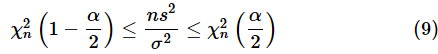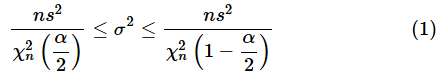［データ分析］母分散の区間推定 〜 スマートフォン利用時間のばらつきはどれぐらい？：やさしい推測統計（区間推定編）
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載（区間推定編）の第3回。今回は正規分布する母集団の分散（＝母分散）を区間推定する方法と考え方を解説します。
連載：
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計（区間推定編）」です。
この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
羽山博筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（区間推定編）、第3回です。前回は区間推定の第一歩として、正規分布する母集団（正規母集団）の平均（＝母平均）の区間推定に取り組みました。今回は正規母集団の母分散を区間推定する具体的な方法とその考え方を見ていきます。
母分散を区間推定するための基本的な考え方
これまで見てきたように、区間推定とは、一定の幅を持たせて母平均や母分散などの母数を推定することでした。その「幅」のことを信頼区間と呼ぶということでしたね。どんな話だったかあやふやだという方は、第1回で解説した、区間推定の基本的な考え方に目を通していただくといいかと思います。
今回は母分散の区間推定を取り上げます。最初に、母分散を区間推定するための大まかな考え方と手順を図解しておきます（図1）。信頼区間の意味として「例えば、95％信頼区間とは、信頼区間を何回も求めたとき、その試行の95％に当たる回に母数が含まれている」ということでした。そのような考え方の下でサンプルから母分散の信頼区間を求めたところ、図1のような結果が得られた、ということです。
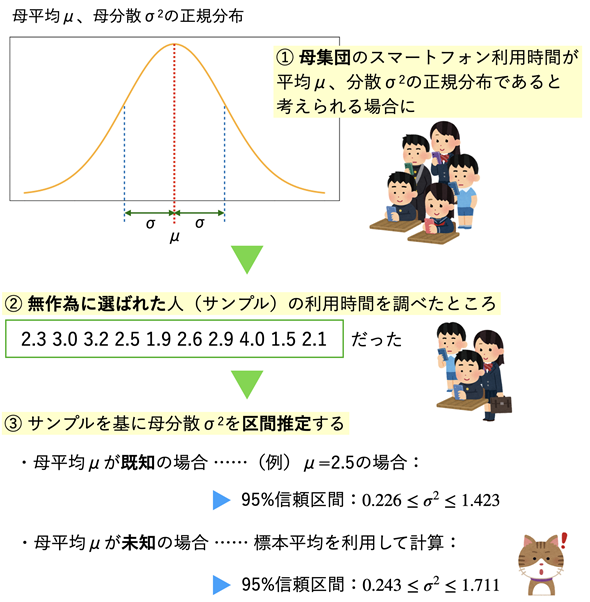図1 母分散を区間推定するための考え方と手順母集団が正規分布するという前提の下、母集団から取り出されたサンプルを基に母分散を区間推定する。母平均μが既知の場合と未知の場合では計算方法が異なることに注意（計算方法は後述）。
図1のデータは架空のデータですが、こども家庭庁の「青少年のインターネット利用環境実態調査（令和5年度）」のデータを参考にしています（クリックするとCSVファイルがダウンロードされます）。スマートフォンでのインターネット利用時間が5時間以上と回答した人が多いので、母集団は正規分布に従うようには見えませんが、その回答者を除外すれば、おおむね正規分布に近い形になっています（実は、シャピロ・ウィルク検定と呼ばれる方法で「正規分布でないとはいえない」（ただし、正規分布であるとは断言できません）という結果を求めてあるのですが、そのお話はまた仮説検定編で）。
ここで重要となるのは、図中にも示したように、母平均μが既知の場合と未知の場合では計算方法が異なることです。もちろん、結果も異なってきます。
実際のところ、母平均μが既知である場合というのはあまり考えにくいのですが、例えば、製品のサイズに基準値が設けられているような場合がそれに当たります。
前回、母平均の区間推定の場合は、母集団が正規分布に従っていなくてもサンプルサイズがおおむね30以上で、極端な外れ値や分布の偏りがなければ、母集団の分布はどのようなものでも構わないというお話をしました。その根拠は中心極限定理でした。しかし、母分散については中心極限定理が適用できないので、そういうわけにはいきません。そのような場合には、ブートストラップ法による推定などが利用できます。最後のコラムで紹介します。
まずは信頼区間を求めるためのそれぞれの式を見ておきましょう。Excelには分散の信頼区間を求めるための関数がないので、以下の式を利用する必要があります。といっても、標本分散や不偏分散、カイ二乗分布のα/2点を求めるためにExcelの関数が使えるので、実際にやってみるとそれほど難しくないことが分かると思います（後で実際にやります）。どの関数を使うかも含めて図解しておきます。
母分散の信頼区間（母平均が既知の場合）
右辺で使う関数も左辺と同様です。
母分散の信頼区間（母平均が未知の場合）
右辺で使う関数も左辺と同様です。
s2については、母平均が既知の場合の標本分散s2と同じ文字を使っていますが、ここでは不偏分散を表すことに注意してください。母分散の不偏推定値を表す
を使ってもいいのですが、母分散のσと紛らわしいので、あえてs2としました（意味を理解していれば、紛らわしくてもきちんと区別できるのですが、念のため）。
では、Excelを使ってサクッと信頼区間を求めてみましょう。
母分散を区間推定してみよう（母平均が既知の場合）
それでは、Excelを使って計算してみます。母平均が既知の場合、母分散の区間推定には（1）式を使います。
サンプルファイルをこちらからダウンロードし、［母分散の区間推定 (母平均が既知)］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。操作方法は図4の後に箇条書きで記します。
図4 VAR.P関数とCHISQ.INV.RT関数を使って母分散の信頼区間を求める自由度nのカイ二乗分布のα/2点と、1−α/2点をCHISQ.INV.RT関数で求め、それぞれの値でns2を割れば、信頼区間の下限と上限が求められる。s2は標本分散なので、VAR.P関数で求める。
手順は以下の通りです。
- セルE4に=VAR.P(B4:B13)と入力する
- セルE7に=CHISQ.INV.RT(E6/2,E3)と入力する
- セルE8に=CHISQ.INV.RT(1-E6/2,E3)と入力する
- セルE9に=E3*E4/E7と入力する
- セルE10に=E3*E4/E8と入力する
- セルE12に=TEXT(E9,"0.000") & "≦σ^2≦" & TEXT(E10,"0.000")と入力する（≦はIMEで「いか」や「いじょう」で変換できます）
CHISQ.INV.RT関数には、引数として自由度と有意水準αの値を指定します（後で補足します）。
セルE12に入力した数式では、TEXT関数を使ってセルE9やセルE10の値を小数点以下3桁までの文字列に変換し、≦σ^2≦という文字列を連結しています。&演算子は文字列を連結する演算子ですね。母分散をσ2ではなく、σ^2と表したのは、単にExcelの数式内で上付き文字が基本的には使えないからです。
結果は、0.226 ≤ σ2 ≤ 1.423となりました。95％信頼区間の意味は「母集団からサンプルを取り出して母数を求め、信頼区間を計算することを何度も繰り返すと、その95％の回に母数が含まれている」ということでした。そのような考え方の下で、サンプルを基に計算した母分散の信頼区間が0.226 ≤ σ2 ≤ 1.423であった、ということですね。
ここでは、カイ二乗分布のα/2点を求めるために、CHISQ.INV.RT関数を使いました。この関数はカイ二乗分布の累積分布関数の右側（上側）確率が何％かになるときのχ2値を求めるものです（図5）。
図5 自由度10のカイ二乗分布の右側2.5％点グラフは自由度10のカイ二乗分布の確率密度関数。オレンジのアミカケの部分の面積が累積確率となる。α＝5％であれば、α/2＝2.5％。CHISQ.INV.RT関数では右側確率が求められるので、このときのα/2％点は、右側（上側）のアミカケ部分が全体の面積の2.5％となるようなxの値のこと。左側（下側）のアミカケ部分の面積は、左から見ると2.5％点だが、ここでは右側から見ているので100−2.5＝97.5％点となる。
区間推定や統計的検定で「α/2点」という表現があった場合、右側確率がα/2となる点を表すのが一般的です。しかし、α/2点が左側確率を意味している場合もあるので、注意が必要です（正規分布やt分布のように左右対称な分布の場合など）。例えば、ExcelのCHISQ.INV関数では左側確率を指定します。従って、CHISQ.INV関数を使うなら、図5に示した1−α/2点を求めたいときにはα/2の値を指定し、α/2点を求めたいときには1−α/2の値を指定する必要があります。なお、紛らわしい場合は右側（上側）α/2点や、左側（下側）α/2点と明記して区別します。
続いて、母平均が未知の場合の母分散の区間推定です。
母分散を区間推定してみよう（母平均が未知の場合）
母平均が未知の場合、母分散の区間推定には（2）式を使います。以下に（2）式を再掲しておきます。
サンプルファイルの［母分散の区間推定 (母平均が未知)］ワークシートを開いて試してみてください。操作方法は図6の後に箇条書きで記します。
図6 VAR.S関数とCHISQ.INV.RT関数を使って母分散の信頼区間を求める自由度n−1のカイ二乗分布のα/2点と、1−α/2点をCHISQ.INV.RT関数で求め、それそれの値で(n−1)s2を割れば、信頼区間の下限と上限が求められる。ここでは、s2は不偏分散なので、VAR.S関数で求める。
手順は以下の通りです。
- セルE4に=VAR.S(B4:B13)と入力する
- セルE7に=CHISQ.INV.RT(E6/2,E3-1)と入力する
- セルE8に=CHISQ.INV.RT(1-E6/2,E3-1)と入力する
- セルE9に=(E3-1)*E4/E7と入力する
- セルE10に=(E3-1)*E4/E8と入力する
- セルE12に=TEXT(E9,"0.000") & "≦σ^2≦" & TEXT(E10,"0.000")と入力する
結果は0.243 ≤ σ2 ≤ 1.711となりました。
母分散の信頼区間はどのように計算されるか
ここからは、（1）式と（2）式がどのようにして導き出されたかをお話しします。実用的には、上で見たように計算ができればいいのですが、やはり、意味も理解しておきたいところです。数式を変形するだけなので、淡々と進めていきます。先ほどと順序は逆になりますが、母平均が未知である場合の方が分かりやすいので、そちらから見ていきます。
母分散の信頼区間を導き出そう（母平均が未知の場合）
母平均が未知の場合、母分散の信頼区間は（2）式で表されました。再掲しておきます。
カイ二乗分布は分散に関連する分布です。このことについては、確率分布編の第7回で詳しく解説しました。母平均が未知の場合、カイ二乗分布の確率変数χ2は、以下の式で表されます。この式では、Xは、具体的な個々の値ではなく、データの値を一般的に表すという意味を強調するために大文字にしてあります。
これが、自由度n−1のカイ二乗分布に従う、ということでしたね。ところで、（3）式の分子に何か見覚えはありませんか。不偏分散s2を求めるための以下の式と見比べてみてください。
（4）式にn−1を掛ければ、（3）式の右辺の分母と一致します。
そこで、（5）式の左辺を（3）式の分子に代入しましょう。以下のようになります。
ここまでは、確率分布編の第7回でも解説しました。このχ2値が「自由度n−1のカイ二乗分布で1−α/2点〜α/2点の範囲に入る」ということを不等式で表せば、以下のようになります。
各項を(n−1)s2で割りましょう。この値は正なので不等号の向きは変わりません。
各項を逆数にします。逆数にすると不等号の向きが変わります。「ん、どういうこと？」と思われるかもしれませんが、2 < 3の例で考えてみると分かりやすいと思います。逆数にすると、1/2 > 1/3のようになり、不等号の向きが変わります。というわけで、以下のようになります。
各項を小さい方から並べると、
となり、（2）式と一致しました。このようにして、信頼区間を求めるための式が導き出されたというわけです。
母分散の信頼区間を導き出そう（母平均が既知の場合）
母平均が既知の場合はどうなるでしょうか。母平均が既知の場合、カイ二乗分布の確率変数は、以下の式で表されました。
これが自由度nのカイ二乗分布に従う、ということでした。では、（7）式の分子と、標本分散s2を求める式を見比べてみましょう。
おや、（7）式ではμを使っているのに、（8）式では
を使っていますね。母平均が未知の場合は(n-1)s2をうまく代入できましたが、この場合は、ns2を（7）式の分子に代入できません。実は、このような場合でも、
のが一般的です。理由は、計算が簡単になるからです。Excelでも標本分散ならVAR.P関数だけで求められますね。
そうすれば、（7）式の分子と（8）式の分子が一致するので、ns2を（8）式の分子に代入できます。それが、自由度nのカイ二乗分布で1−α/2点〜α/2点の範囲に入ることを不等式で表すところまでを書くと以下のようになります。
後は、（9）式をσ2について解くだけです。この後の流れは母平均が未知の場合と全く同じなので省略します。というわけで、（1）式の
が導き出されます。
コラム 正規分布でない場合に分散の区間推定を行う
母分散の区間推定では、母集団が正規分布に従っていない場合にはブートストラップ法などによる推定が利用できる、といったお話を最初にしました。
ブートストラップ法では、サンプルの抽出を重複ありで何度も繰り返して（リサンプリングして）信頼区間を求めます。Excelでは大量のセルを使わないといけないので、紙面では割愛しますが、サンプルファイルの［ブートストラップ法］ワークシートに作成例を含めておきます。
リスト1は、Pythonでブートストラップ法を実行するプログラムを書いた例です。コードの詳細については解説しませんが、コメントを見ればやっていることは大体分かると思います。サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。
# ブートストラップ法
import numpy as np
# データ
data = np.array([2.3, 3.0, 3.2, 2.5, 1.9, 2.6, 2.9, 4.0, 1.5, 2.1])
n_bst = 10000 # ブートストラップの回数
bst_var = [] # サンプルの不偏分散を記録するリスト
np.random.seed(0) # 乱数の種を固定
# データから10個のサンプルを重複ありで、n_bst回取り出す
for _ in range(n_bst):
sample = np.random.choice(data, size=10, replace=True)
# 不偏分散を計算して、リストに追加する
bst_var.append(np.var(sample, ddof=1))
# 全ての不偏分散を基に信頼区間を計算（95％信頼区間）
interval = np.percentile(bst_var, [2.5, 97.5]) # パーセンタイル値を求める
print(interval)
np.random.choiceでリサンプリングを行っている。replace=Trueという設定により、重複ありで10個リサンプリングされる。重複ありということは、例えば、2.3という値が複数回取り出されたり、3.0という値が取り出されないこともある。ブートストラップ法にもさまざまな種類があるが、この例では得られた全ての不偏分散について、2.5パーセンタイル値〜97.5パーセンタイル値の範囲を求める最もシンプルな方法を使っている（97.5パーセンタイルとは、データを小さい順に並べたとき、全体のうち、順位が下位から97.5パーセントの位置にある値のこと。該当する位置に値がない場合は補間によって求められる）。
上のコードを実行すると、[0.128425 0.90625833]という結果が得られます。
今回は、母分散の区間推定について、計算の手順から信頼区間を表す式の意味までを解説しました。前回と今回で、区間推定の基本的な考え方や信頼区間を表す式がどのように導き出されるかがだいたい分かったと思います。
ただ、これまでちらほらと名前が登場しているベイズ統計の確信区間が気になっている方もおられるのではないかと思います。そこで、次回は番外編として、ベイズ統計の確信区間について見ていきます。とはいえ、ベイズ統計を一から説明するわけにはいかないので、基本的な考え方と計算の手順を中心にお話しします。次回もお楽しみに！
Copyright© Digital Advantage Corp. All Rights Reserved.
注目のテーマ
ITmediaはアイティメディア株式会社の登録商標です。