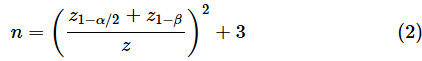【Excelで学ぶデータ分析】中古車の排気量と価格には関係があるか？（相関係数の検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第8回。今回は、相関係数の検定方法について解説します。

» 2025年12月11日 05時00分公開

連載：

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第8回です。前回は、独立性の検定を紹介しました。例えば、出身地域と麺類の好みは独立しているか（＝関係がないか）どうかを調べました。

　今回は相関係数の検定を取り上げます。独立性の検定では名義尺度であるカテゴリの度数（人数など）を基に検定を行いましたが、相関係数の検定では間隔尺度である変数の値を基に、それらの関係を調べます。今回は、中古車の排気量と価格を例に、それらの変数に相関があるかどうかを調べます。この検定は帰無仮説が「相関はない」なので、一般に無相関の検定と呼ばれます。

相関係数の検定についての基本的な考え方

　相関係数については、統計学の初歩で登場する考え方なので、初見だという方は少ないと思います。相関係数は変数同士の関係の強さを表す値でした。それについては『やさしいデータ分析』の第13回で「気温と電気代の関係」という例を基に、相関係数の意味や計算の方法、落とし穴などについて詳しく解説しました。また、この連載の『区間推定編』の第7回では、「体格指数と糖尿病の進行度」という例で、信頼区間の求め方も解説しました。

　今回は中古車の排気量と価格を例に相関係数を求め、相関があるかどうかを検定します。図1のイメージでは、実在の車名と排気量を掲載していますが、本体価格は架空のものです。

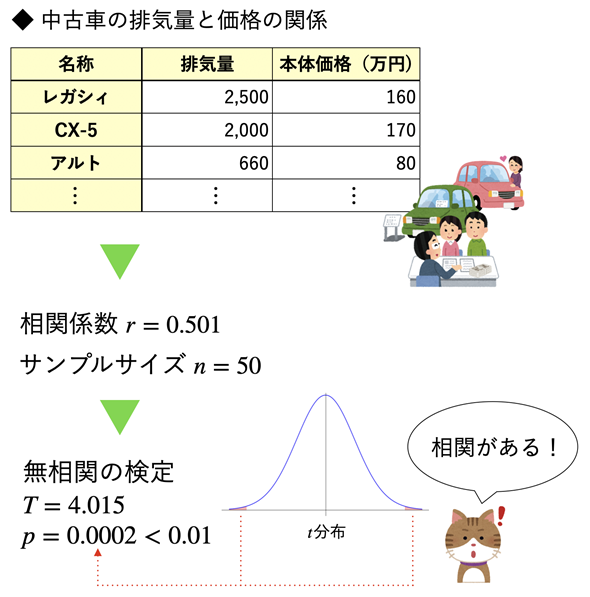図1　中古車の排気量と価格に相関はあるのか？
相関係数はCORREL関数を使えば簡単に求められるが、その値から「相関がある」と言えるかどうかを調べたい。相関係数は正の場合と負の場合が考えられるので、今回は両側検定を行う。利用する値は相関係数とサンプルサイズ、利用する分布はt分布。

　それでは、帰無仮説と対立仮説の確認から始めましょう。上でも触れたように、帰無仮説が「相関はない」なので、相関係数の検定は無相関の検定と呼ばれます。サンプルから得られた相関係数rと区別するために、母相関係数をρ（ローと読みます）と表します。

帰無仮説（H₀）：排気量と本体価格に相関はない（ρ＝0）
対立仮説（H₁）：排気量と本体価格に相関がある（ρ≠0）

　母相関係数ρが0でないことを確かめたいので、両側検定となります。常識的に考えて、排気量が大きければ本体価格も高い（正の相関がある：r>0）と想定されるので片側検定でもいいのですが、無相関の検定では両側検定とするのが一般的です。

相関係数の検定を行ってみよう

　無相関の検定での検定統計量Tは以下の式で求められます。

　検定統計量Tが求められたら、t分布の両側確率を求めます。かなり範囲が小さいので見づらいですが、図1の中に掲載したグラフで、両端のピンク色の部分の面積が両側確率に当たります。t分布の両側確率はT.DIST.2T関数で求められますが、T.DIST.2T関数には正の値を指定する必要があるので、実際にはTの絶対値を指定します。自由度にはn－2を指定します。

　では、こちらからダウンロードしたExcelファイルを開いて試してみてください。［無相関の検定］ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

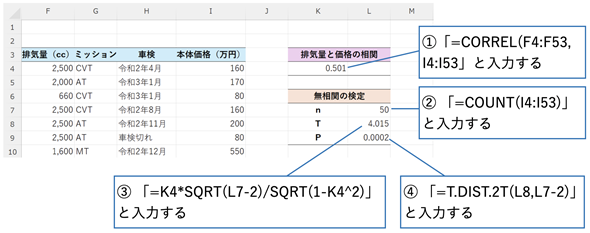図2　相関係数とサンプルサイズを基に、無相関の検定を行う
排気量と価格を見やすくするために図ではF列以降のみを表示してある。データは50件（4行目～53行目まで）入力されている。セルK4でCORREL関数を使って相関係数を求め、セルL7ではCOUNT関数を使ってサンプルサイズを求めている。それらの値を基に、（1）式に従ってセルL8で検定統計量を求める。セルL9でT.DIST.2T関数を使ってP値を求めている。

　セルL8では、相関係数とサンプルサイズを基に（1）式に従って検定統計量Tを求めています。続いて、セルL9でT.DIST.2T関数にTの値と自由度（n－2）を指定し、P値を求めます。結果は、P＝0.0002<0.01となったので、帰無仮説H₀を棄却し、対立仮説H₁を採用します。従って、「排気量と本体価格には相関がある」と言えます。

無相関の検定での落とし穴

　無相関の検定のみならず、統計的検定にはサンプルサイズが大きくなると、有意になる（P値が小さくなる）という性質があります。（1）式をもう一度見てみましょう。

　検定統計量Tは相関係数rとサンプルサイズnで決まります。（1）式の分子に注目すると、rの値が同じでも、nの値が大きくなるとTの値が大きくなることが分かります。Tが大きくなると、P値は小さくなります。図形的に見るなら、Tが大きくなると、図1の両側のピンク色の部分の境界が端の方にずれていくということです（図3）。

図3　検定統計量Tが大きくなるとP値は小さくなる
検定統計量Tは横軸の値。T＝2の場合（左）とT＝3の場合（右）で、両側確率を可視化してみた。Tが大きくなるとP値は小さくなる。nが大きくなると（1）式からTが大きくなり、P値が小さくなることが分かる。

　さらに、nの値とP値の関係を可視化してみましょう（図4）。［サンプルサイズとP値］ワークシートを開いて試してみてください。図を見やすくするために、手順は図の後に箇条書きで記します。

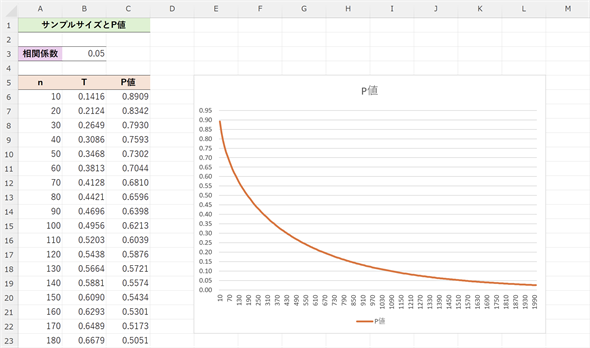図4　サンプルサイズnが大きくなるとP値は小さくなる
作成手順は後の箇条書きに記すこととして、ここでは、グラフに注目してほしい。相関係数が0.05でも、n＝1510辺りでPの値が0.05となっている（正確にはn＝1538でP＝0.0499<0.05となる）。

　手順は以下の通りです。

セルA6に「=SEQUENCE(200,1,10,10)」と入力する（200行1列に、10から10刻みで連続値を作る。セルA6～A205に値が表示される）
セルB6に「=B3*SQRT(A6#-2)/SQRT(1-B3^2)」と入力する
- Google スプレッドシートの場合はセルB6に「=ARRAYFORMULA((B3*SQRT(A6:A205-2)/SQRT(1-B3^2)))」と入力する
セルC6に「=T.DIST.2T(B6#,A6#-2)」と入力する
- Google スプレッドシートの場合はセルB6に「=ARRAYFORMULA(T.DIST.2T(B6:B205,A6:A205-2))」と入力する

　サンプルファイルでは、上記の数式を入力すると、グラフが自動的に描画されるようになっています。自分でグラフを作成したい方はサンプルファイル中に手順を記してあるので、それを参考に試してみてください。

　表作成の手順が長くなりましたが、ここで重要なのはサンプルサイズnが大きくなると、P値が小さくなるということでしたね。上の例では、相関係数rがわずか0.05であるにもかかわらず、n＝1510辺りで、P値がほぼ0.05になってしまいます。そういうわけで、サンプルサイズが大きくなれば、いちいち検定を行うまでもなく、『やさしいデータ分析』の第13回で紹介した目安の値で評価するのが妥当です。公的機関などの調査で数千～数万のサンプルを採った場合に、検定を行わないのはそのためでもあります。

　では、検定を行うにはどの程度のサンプルサイズが必要なのでしょうか。次にサンプルサイズの見積もりについて見ていきましょう。

無相関の検定での適切なサンプルサイズは？

　この連載では、検定の方法をメインに解説しているので、適切なサンプルサイズを求める方法を記事の後半で紹介していますが、実際には、実験や調査の前にサンプルサイズを決めておくのがスジです（このこともおさらいですが、念のため）。大規模な調査で、サンプルサイズが大きくなる場合は、上でお話ししたように検定の必要はありません。実験や調査の性格上、サンプルサイズが大きく採れない場合に検定が役に立つということです。サンプルサイズの見積もりも、そのような制約の中でどの程度の大きさが妥当かということになります。

　相関係数の検定での、適切なサンプルサイズnは以下の式で近似的に求められます。

　zという文字が異なる意味で幾つか登場しているので紛らわしいですが、分子のz_1－α/2は標準正規分布の1－α/2点の値、z_1－βは標準正規分布の1－β点の値です。一方、分母のzは、相関係数をフィッシャー変換した値です。つまり、

です。相関係数は定義域が－1～1で、分布に偏りがあります。そのため、フィッシャー変換を行うことにより正規分布に近づけるというわけです。フィッシャー変換の詳細については、こちらのグラフなどを参照してください。

　ただし、Excelでは（3）式に従って計算しなくても、FISHER関数に相関係数rの値を指定するだけでzの値が求められます。では、（2）式に従って、r＝0.5と想定される場合に必要なサンプルサイズを求めてみましょう。ここでは、有意水準α＝0.01、検出力1－β＝0.95で計算してみます。［サンプルサイズの見積もり］ワークシートを開き、図5のように操作します。

図5　無相関の検定でのサンプルサイズを見積もる
セルB7で標準正規分布の1－α/2点の値を求め、セルB8でz_1－βは標準正規分布の1－β点の値を求める。セルB9では、セルB3に入力されている相関係数をFISHER関数でフィッシャー変換する。セルB10で（2）式に従ってサンプルサイズを計算する。

　サンプルサイズの見積もりをより正確に行うには、非心t分布を利用する必要があります。検出力が1－β以上になるnの値を求めるPythonのプログラムをこちらに作成してあるので、興味のある方はご参照ください。最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行するとn=57という結果が表示されます。

　実用的には第6回で紹介したG*Powerを使うのが簡単です。検定の方法などは以下のように指定します。

Test family： t tests
Statistical test： Correlation: Point biserial model
Type of power analysis： Compute required sample size - given α, power, and effect size

　といっても、これらを一つ一つ指定するよりは、メニューバーから［Tests］-［Correlation and regression］-［Correlation: Point biserial model］を選択するのが簡単です。

　上記の指定ができたら、［Tail(s)］リストで［Two］を選択し（両側検定という意味）、［Effect size |ρ|］ボックスに、想定される母相関係数として0.5を入力します。続けて、［α err prob］ボックスに0.01、［Power (1-β err prob)］ボックスに0.95を入力して［Calculate］ボタンをクリックすれば、［Total sample size］として57という値が表示されます。

　z近似よりも少し小さな値になりましたが、サンプルサイズの見積もりはあくまでも目安です。「より正確に行うには、非心t分布を……」とお話ししましたが、57という値が出たからといって、忠実にその値を守る必要はありません。キリのいい60という値や、z近似で得られた63という値を基に、さらに余裕を持たせて65などとしても構いません（実際に調査や実験を行うと欠損値がある場合も考えられるので、多少の余裕を見ておいた方がいいと思います）。

　今回は、相関係数の検定について、その考え方や方法を解説しました。併せて、検定の落とし穴やサンプルサイズの見積もりについて、おさらいや落とし穴の確認なども含めてお話ししました。ところで、中古車の価格は排気量だけでなく、年式や走行距離などによっても変わります。

　そこで、次回は、それらの説明変数を利用した回帰分析を取り上げ、回帰式の当てはまりの良さについての検定を行います。次回もお楽しみに！

「やさしい推測統計（仮説検定編）」