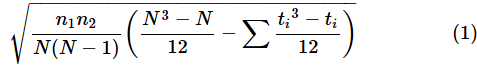【Excelで学ぶデータ分析】業界によって初任給に差があるか？（中央値の差の検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第11回。今回からノンパラメトリック検定に取り組みます。まず、中央値の差を検定する方法について解説します。

» 2026年01月28日 05時00分公開

[羽山博，著]

この記事は会員限定です。会員登録（無料）すると全てご覧いただけます。

連載目次

連載：

『社会人1年生から学ぶ、やさしい推測統計（仮説検定編）』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第11回です。前回までは母集団の分布が何らかの母数（パラメーター）で決まる場合の検定、つまりパラメトリック検定の方法を解説してきました。

　今回からは、母集団に特定の母数を仮定しない（できない）場合の検定方法について解説します。そのような検定をノンパラメトリック検定と呼びます。今回は順位を基にした中央値の差の検定を取り上げます。

中央値の差の検定とは？

　中央値の差の検定としては、ウィルコクソンの順位和検定やマン・ホイットニーのU検定が利用できます。計算の手順は異なりますが、それらの検定は実質的に同じものです。今回はマン・ホイットニーのU検定により、中央値の差を検定します。以下、単にU検定と呼びます。

　中央値の差の検定は、母集団の正規性は前提としませんが、分布が同じ形であると考えられる場合の検定です。母集団の分布の形が異なる場合は、中央値の差ではなく、分布のズレを検定していることになります。中央値の差の検定は図1のようなイメージです。

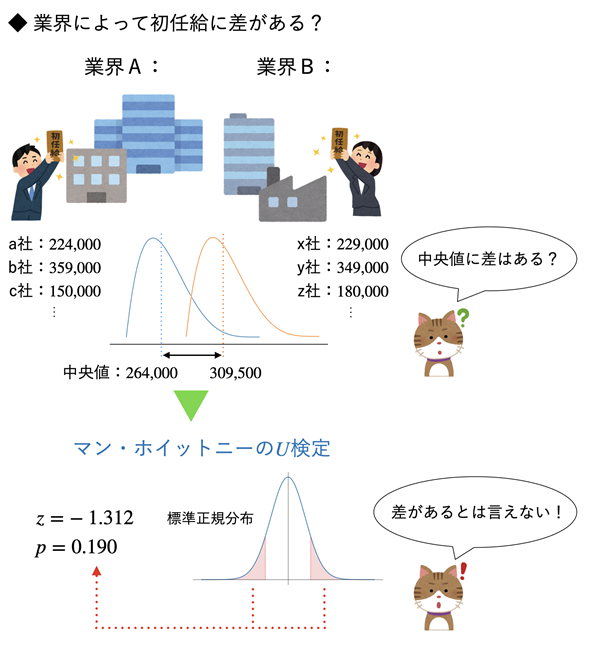図1　業界によって初任給に差はあるか？
中央値の差の検定では、順位を基に検定統計量zを求め、標準正規分布の両側確率または片側確率を求めるとよい。今回は、対立仮説を「中央値は異なる」とするので、両側検定を行う。

　例によって、帰無仮説と対立仮説の確認から始めます。

帰無仮説（H₀）：中央値は等しい
対立仮説（H₁）：中央値は等しくない

　この例では、分布の形が同じであるという前提なので、上のような帰無仮説と対立仮説になりますが、前述したように、分布の形が異なる場合は、帰無仮説は「分布は同じである」、対立仮説を「分布にはズレがある」などのように表されます。

中央値の差を検定してみよう～マン・ホイットニーのU検定

　残念ながらExcelにはU検定を行う関数がありません。そのため、以下のような手順に従ってP値を計算する必要があります。それぞれの群のサンプルサイズをn₁, n₂とすると、

2群のサンプルをまとめて順位を付ける
各群の順位の和を求める（W₁,W₂とする）
U₁＝W₁－n₁(n₁＋1)/2の値を求める
U₂＝W₂－n₂(n₂＋1)/2の値を求める
U₁とU₂の小さい方について、以下の計算を行う（ここでは、U₁が小さい方とする）
分子の値として、U₁ － (n₁＋n₂)/2 ＋ 0.5の値を求める

検定統計量zを上の分子／分母で求める
zに対する標準正規分布の両側確率を求める

となります。ただし、上の手順は同順位がない場合のものです。同順位がある場合については後述します。

　分子の値に0.5を加えるのは、離散値を連続値として扱うための補正（連続値補正）です。

　では、こちらからダウンロードしたExcelファイルを開いて試してみてください。［U検定］ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。操作方法は図の後に箇条書きにしておきます。上の手順と照らし合わせて操作してみてください。

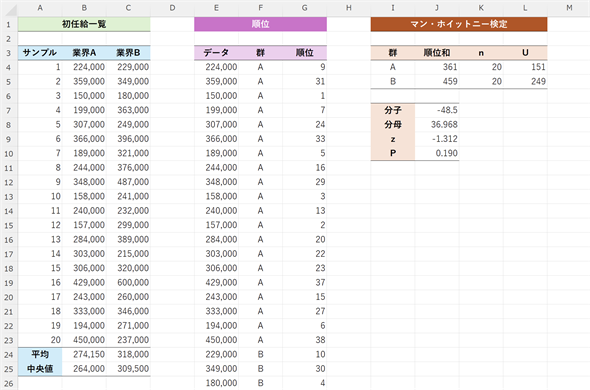図2　中央値の差を検定する
B列とC列には、2つの業界での各企業の初任給が入力されている（いずれも左側にやや偏った分布となっている）。E列で2群のデータをまとめ、G列で全体での順位を付ける（画面では表示を省略してあるが、E列～G列は43行目まで値が並ぶことになる）。続いて、セルJ4とJ5で各群の順位の和を求め、L列でUの値を求める。さらに、Uとnの値を基に、セルJ7で分子の値を、セルJ8で分母の値を求め、セルJ9でzの値を求める。zの値が得られれば、セルJ10で標準正規分布の両側確率が求められる。具体的な操作方法は以下の箇条書きを参照。

　結果は、P＝0.190となり、帰無仮説は棄却できませんでした。つまり「中央値に差があるとは言えない（分布の形が異なる場合には「分布にズレがあるとは言えない」）」ということになります。セルB25とC25で求めた中央値を見ると、業界Aの初任給は26万4000円で業界Bの初任給は30万9500円と、業界Bの方がよさそうですが、これだけでは何ともいえないということですね。

　具体的な操作方法は以下の通りです。

セルE4に「=VSTACK(B4:B23,C4:C23)」と入力する（2群のデータを1つにまとめる）
F列の群は手作業で入力する（関数を使って求めることもできなくはないが、コピーした方が簡単）。
セルG4に「=RANK.AVG(E4:E43,E4:E43,1)」と入力する（順位が求められる）
セルJ4に「=SUMIF(F4:F43,I4,G4#)」と入力する（A群の順位和W₁が求められる）
セルJ5に「=SUMIF(F4:F43,I5,G4#)」と入力する（B群の順位和W₂が求められる）
セルK4に「=COUNT(B4:B23)」と入力する（n₁の値が求められる）
セルK5に「=COUNT(C4:C23)」と入力する（n₂の値が求められる）
セルL4に「=J4-K4*(K4+1)/2」と入力する（U₁＝W₁－n₁(n₁＋1)/2の値が求められる）
セルL5に「=J5-K5*(K5+1)/2」と入力する（U₂＝W₂－n₂(n₂＋1)/2の値が求められる）
セルJ7に「=L4-(K4*K5)/2+0.5」と入力する（分子の値が求められる）
セルJ8に「=SQRT(K4*K5*(K4+K5+1)/12)」と入力する（分母の値が求められる）
セルJ9に「=J7/J8」と入力する（検定統計量zの値が求められる）
セルJ10に「=(1-NORM.S.DIST(ABS(J9),TRUE))*2」と入力する（両側確率が求められる）

　Google スプレッドシートでは、配列数式を使う場合に式全体をARRAYFORMULA関数の引数に指定する必要があります。また「G4#」といったスピル機能で得られた範囲の指定ができないので、「G4:G43」のようにセル範囲を指定する必要があります。また、Google スプレッドシートのNORM.S.DIST関数は累積分布関数の値を求めるためのものなので、関数の形式を指定するための第2引数は不要です。つまり、セルJ10には「=(1-NORM.S.DIST(ABS(J9)))*2」と入力します。詳細については、Googleスプレッドシートでの作成例を参照してください。

同順位がある場合の補正を行う

　U検定では、同順位に平均の順位を与えます。例えば、3位の値が2つあれば、そのそれぞれに3位と4位の平均である3.5という順位を与え、次を5位とします。つまり、1, 2, 3.5, 3.5 ,5, ...という順位になります。これについては、RANK.AVG関数を使えば簡単に求められます（上の例には同順位はありませんが、やはりRANK.AVG関数を使っています）。従って、順位の求め方は上で見た方法と全く同じです。

　ただし、検定統計量を求める際の分母に当たる値を補正する必要があります。補正のための式は以下の通りです。Nは全体のサンプルサイズ（つまりn₁＋n₂）で、t_iはi番目の同順位の個数です。

　例えば、順位が1, 2, 3.5, 3.5, 5, 7, 7, 7, 9であれば、2つの同順位と3つの同順位があるので、t₁＝2,t₂＝3を（1）式に当てはめます。しかし、Excelでこの計算を行うのは、かなり面倒です。一応、サンプルファイルの［U検定（同順位）］ワークシートに計算例と手順の説明を含めておきましたが、何もExcelにこだわる必要はありません。もっと便利な方法を次に紹介します。

マン・ホイットニーのU検定はPythonを使うと簡単にできる！

　上で見たように、Excelを使ってU検定を行うためには、かなり長い手順を踏む必要がありました。また、同順位がある場合の補正も絶望的なまでに面倒です。実際には、Pythonなどでプログラミングを行った方がはるかに簡単です。「プログラミング」というだけで、ちょっと敬遠する人もいるかもしれませんが、利用するモジュールを指定し、データを準備して、検定のための関数を呼び出すだけです。上の例であれば、以下のようなコードになります。

from scipy.stats import mannwhitneyu

# データ（同順位がないデータ）
x = [224000, 359000, 150000, 199000, 307000,
     366000, 189000, 244000, 348000, 158000,
     240000, 157000, 284000, 303000, 306000,
     429000, 243000, 333000, 194000, 450000]
y = [229000, 349000, 180000, 363000, 249000,
     396000, 321000, 376000, 487000, 241000,
     232000, 299000, 389000, 215000, 320000,
     600000, 260000, 346000, 271000, 237000]

# マン・ホイットニーのU検定
u, p = mannwhitneyu(x, y, alternative='two-sided')

# 結果の表示
print(f"P={p:.3f}") # P=0.190という結果が得られる

U検定を行うためのコード
scipy.statsモジュールのmannwhitneyu関数を利用する。xとyを指定し、両側検定の場合はalternative引数に'two-sided'を指定する。片側検定の場合は'less'か'greater'を指定すればよい。既定では、サンプルサイズが小さく（8以下）、同順位がない場合には、連続性補正が行われないが、それ以外の場合は連続性補正が行われ、同順位がある場合の補正も行われる。

　上のコードはこちらにあります。リンクを開くとPythonのプログラムが表示されるので、最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してプログラムを実行すると、P=0.190という結果が表示されます。

　同順位があるデータでの例は2番目のコードセルに入力してあります。データが異なるだけで、mannwhitneyu関数の指定は全く同じです。同順位がある場合の補正も自動的に行われるので、Excelを使うよりもはるかにラクですね。

中央値の差を検定する際の適切なサンプルサイズは？

　本来なら、サンプルを収集する前に効果量などを見積り、サンプルサイズを決めておくのがスジですが、この連載では検定の方法を理解することをメインにお話ししているので、今回も検定の方法を先に解説しました（ということは何度もお話ししていますね）。

　中央値の差の検定では、母集団の分布を仮定していないので、サンプルサイズを求めるための決まった公式がありません。一般に、t検定でのサンプルサイズの求め方を利用し、効果量を補正して適用する方法がよく使われます。第6回で紹介したG*Powerでもその方法が使われています。まず、利用例を見てみましょう（図3）。手順は画面の後に箇条書きで記しておきます。

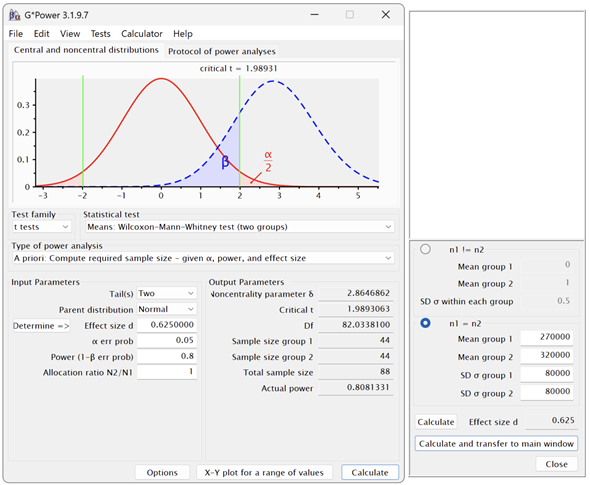図3　G*Powerにより、U検定に必要なサンプルサイズを求める
各群であらかじめ見積もった平均と標準偏差を基に、効果量dを計算し、d＝0.625とした（やや大きめの効果量）。有意水準α＝0.05、検出力1－β＝0.8で、両側検定とした場合の例で計算する。結果は各群44となった。

　G*Powerでの操作手順は以下の通りです。検定の方法などを以下のように選択します。

［Test family］のリストから「t tests」を選択する
［Statistical test］のリストから「Means: Wilcoxon-Mann-Whitney test (two groups)」を選択する
［Type of power analysis］のリストから「Compute required sample size - given α, power, and effect size」を選択する

　メニューバーから［Tests］－［Means］－［Two independent groups: Wilcoxon (non-parametric)］を選択しても同じ設定になります。

　上記の指定ができたら、以下のように操作します。

［Tail(s)］リストから［Two］を選択する
［Determine =>］ボタンをクリックする
右側に表示されたパネルで［n1=n2］オプションを選択する
［Mean group 1］ボックスに、想定されるA群の平均として270000を入力する
［Mean group 2］ボックスに、想定されるB群の平均として320000を入力する
［SD σ group 1］ボックスに、想定されるA群の標準偏差として80000を入力する
［SD σ group 2］ボックスに、想定されるB群の標準偏差として80000を入力する
［Calculate and transfer to main window］ボタンをクリックする（左側のウインドウの［Effect size d］ボックスに、効果量として0.6250000という値が表示される）
［α err prob］ボックスに0.05と入力する
［Power (1-β err prob)］ボックスに0.8と入力する
［Calculate］ボタンをクリックする