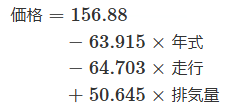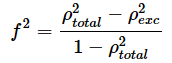【Excelで学ぶデータ分析】年式、走行距離、排気量のどれが中古車の価格予測に役立つのか？（重回帰式の係数の有効性を検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第10回。今回は、重回帰分析における回帰式の係数の有効性を検定する方法について解説します。

» 2026年01月14日 05時00分公開

連載：

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第10回です。前々回は、中古車の排気量と価格の例で相関係数の検定を行い、前回は中古車の年式、走行距離、排気量を説明変数として、重回帰分析により価格の予測を行った際の、回帰式の当てはまりの良さを検定しました。今回も同じ事例を使うので続けて読んでくださっている方には代わり映えがしない気がするかもしれませんが、今回は回帰式の係数の有効性についての検定を行います。この検定では、結果の解釈や利用にはこれまで以上に大きな落とし穴がありますが、それについては検定の方法を解説した後で紹介します。

回帰式の係数の有効性を検定するには？

　中古車の事例で回帰式を具体的に表すと以下のようになっていました。

　今回の目標は、このような式の係数（a₁,a₂,a₃）が本体価格の予測に役立つかどうかを調べたいということです（図1）。

図1　年式、走行、排気量の係数のどれが価格の予測に役立つのか？
係数の有効性の検定は、それぞれの係数が0であるかどうかの検定となる。LINEST関数で求めた標準誤差を基に検定統計量Tを計算し、T.DIST.2T関数で両側確率を求めるとよい。

　例によって、帰無仮説と対立仮説の確認から始めます。係数が「有効ではない」というのはその係数が0である、ということなので、以下のように表せます。

帰無仮説（H₀）：回帰式の係数a_i＝0
対立仮説（H₁）：回帰式の係数a_i≠ 0

　対立仮説は、係数が0でないということなので、両側検定となります（あらかじめ係数の符号が分かっているのであれば、片側検定でも構いません）。

係数の有効性を検定してみよう

　係数の有効性の検定では、LINEST関数によって求めた標準誤差を基に、まず、検定統計量Tを「係数／標準誤差」で求めます。続いて、T.DIST.2T関数にTの値と自由度を指定し、両側確率（P値）を求めます。サンプルサイズをn、説明変数の個数をkとしたとき、自由度はn－k－1となります。自由度の計算は簡単ですが、これもLINEST関数で求められています。

　では、こちらからダウンロードしたExcelファイルを開いて試してみてください。［係数の検定］ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。なお、データには実在の車名を記載していますが、価格などの値は架空のものです。

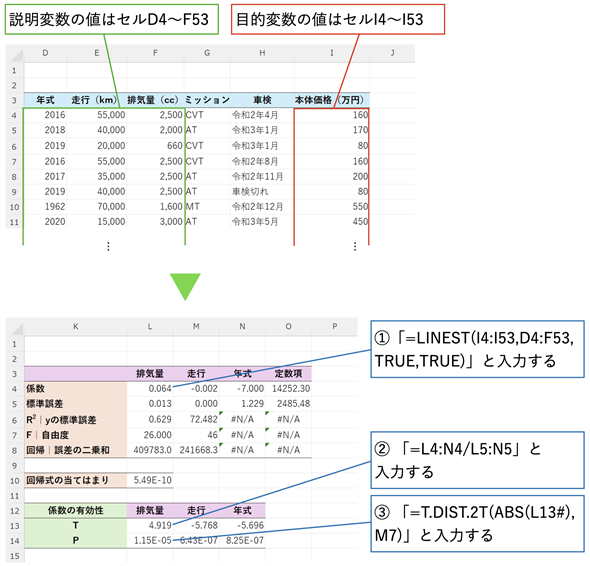図2　回帰式の係数の有効性を検定する
表を見やすくするために、上にサンプル（D列～I列）を、下に重回帰分析の結果と検定結果（L列～O列）を分けて示してある（サンプルファイルではこれらの表は横に並んでいる）。まず、セルL4にLINEST関数を入力し、係数や定数項、補正項を求める。次に、セルL13に「=L4:N4/L5:N5」と入力して、セルL4～N4で求められた係数をセルL5～N5の標準誤差で割り、検定統計量Tを求める。最後に、セルL14に「=T.DIST.2T(ABS(L13#),M7)」と入力して、それぞれのP値を求める。

　LINEST関数を使って回帰式の係数や補正項を求める方法は前回と同じです。おさらいを兼ねて確認しておきましょう。セルL4に入力したLINEST関数には、説明変数の範囲、目的変数の範囲、定数項を求めるかどうか（求める場合はTRUE）、補正項を求めるかどうか（求める場合はTRUE）を順に指定します。

　LINEST関数によって求められた回帰式の係数は、説明変数の列とは逆順に表示されます。ここでは、説明変数が「年式」「走行」「排気量」の順なので、LINEST関数で求めた係数は、「排気量」「走行」「年式」の順に並び、その後に定数項の値が表示されます（セルL4～O4）。

　それぞれの説明変数は単位が異なるので、そのままでは係数の比較がしづらくなります。そのような場合は、説明変数を標準化して重回帰分析を行うといいでしょう。［係数の検定（標準化）］ワークシートに、標準化を行った例を解説とともに含めてあります。標準化を行った場合の回帰式は以下の通りです。

　どの説明変数にどの程度の重みがかかるかがよく分かりますね。以降で求める検定統計量Tの値やP値は標準化を行わない場合と全く同じです。

　さて、ここからが係数の有効性の検定です（定数項についての有効性の検定にはあまり意味がないので、検定の対象からは外すこととします）。セルL5～O8に表示された補正項のうち、各係数に対する標準誤差（セルL5～N5）を利用し、検定統計量Tを「係数／標準誤差」で求めます。上の例では、セルL13に「=L4:N4/L5:N5」と入力し、スピル機能により結果を一括して求めています。

　後は、セルL14にT.DIST.2T関数に検定統計量Tの値（セルL13～N13）と自由度（セルM7）を指定してP値を求めるだけです。ただし、Tの値は負になることもあるので、ABS関数により絶対値を指定します。「=T.DIST.2T(ABS(L13#), M7)」の「L13#」はセルL13の配列数式でスピル機能により求められた範囲（つまり「L13:N13」）を表します。

　スピル機能に不慣れな方は、セルL13に「=L4/L5」と入力して、セルN13までコピーした後、セルL14に「=T.DIST.2T(ABS(L13), $M$7)」と入力して、セルN14までコピーしても同じ結果が得られます。なお、Googleスプレッドシートで配列数式を使う場合は、ARRAYFORMULA関数の引数に数式を指定します。例えば、セルL13には「=ARRAYFORMULA(L4:N4/L5:N5)」と入力します（以降の例でも同じです）。

　結果は、「排気量」「走行」「年式」のいずれについても、きわめて小さな値となりました。P<0.001で有意となり、帰無仮説が全て棄却されるので、いずれの係数も有効であると考えられます……と、言いたいところなのですが、この例ではt検定を3回行っていることになり、第一種の誤差が蓄積してしまいます。

　第一種の誤差α（帰無仮説が正しいのに誤って棄却してしまう確率）を0.05としたとき、帰無仮説を正しく棄却できる確率は1－0.05＝0.95となります。n回の検定を繰り返して行うと、全ての検定で帰無仮説を正しく棄却できる確率は0.95ⁿです。ということは、少なくとも1回の検定で帰無仮説を誤って棄却してしまう第一種の誤差の確率は1－0.95ⁿとなります。上の例では、1－0.95³ ≈ 0.143、つまり、14.3％にもなってしまうというわけです。

　検定を繰り返すことによって第一種の誤差が蓄積する場合には、P値の補正を行います。方法は幾つかありますが、最も簡単なのはボンフェローニ（Bonferroni）の補正です。ボンフェローニの補正では有意水準を検定の回数で割ります。今回の事例では、3つの説明変数について検定を行っているので、3で割ります。例えば、事前に有意水準αを0.01と見積もっていた場合には、α＝0.01/3 ≈ 0.0033とします。実際のところ、図2の例ではP値が極めて小さく、いずれもP<0.001なので、α＝0.0033と設定した場合でも全て有意となります。

　ボンフェローニの補正では有意水準がかなり厳しくなり、検出力が低くなります。やや緩やかに補正する方法としては、ホルム（Holm）の方法があります。この方法では、P値を小さい順に並べ、検定の回数を1ずつ減らしながらαの値を割っていきます。図2の例だと意味が分かりにくいので、別の値を使って説明します。

　例えば、α＝0.05で、P値が小さい順にP₁＝0.01, P₂＝0.015, P₃＝0.03, P₄＝0.04だったとします。このとき、以下のように判定します。

P₁： α＝0.05 / 4 ＝ 0.0125とする。0.01 < 0.0125なので有意
P₂： α＝0.05 / 3 ≈ 0.0167とする。0.015 < 0.0167なので有意
P₃： α＝0.05 / 2 ＝ 0.025とする。0.03 > 0.025なので有意差なし
P₄：上で有意差なしとなったので、以降は見ない（有意差なし）

　図2の事例で、ボンフェローニの補正とホルムの補正を行った例は、［係数の検定（作成例）］ワークシートに含めてあります。

　また、係数の点推定値やP値だけにこだわらず、信頼区間を併せて示すことも重要です。信頼区間は以下の式で求められます。a_iは各係数（の点推定値）で、t_n－k-1(α/2)は自由度n－k-1のt分布でのα/2点の値、SE_iは各係数の標準誤差です。

　上の式で求めた信頼区間についても、［係数の検定（作成例）］ワークシートに含めてあります。

　ところで、検定統計量Tを求めるために使った標準誤差がどのような値で、どのようにして求められるのか気になっている方もおられると思います。イメージ的には「サンプルを何度も採ったときに、その係数がどの程度ばらつくか」といったところですが、自分で式を立てて計算するのはかなり面倒です。サンプルファイルの［標準誤差］ワークシートに計算例と簡単な説明を記しておくこととし、ここでは説明を割愛します。

　検定統計量Tは「係数／標準誤差」なので、係数が大きくても、その説明変数の標準誤差（ばらつき）が大きければ、その係数はあまりアテにならないことが分かりますね。逆に、標準誤差が小さくなれば、Tの値が大きくなり、その場合はP値が小さくなることが分かります。

係数の有効性の検定における落とし穴

　上で見たように、重回帰分析における係数の有効性を検定する場合には、第一種の誤差が蓄積する問題があります。それ以外にも、幾つかの落とし穴があるので、整理しておきましょう。

検定結果によって後からモデルそのものを変えてはいけない

　今回の例では、いずれの係数も有効であると考えられますが、帰無仮説が棄却できない場合に陥りがちな大きな落とし穴があります。仮に、上の例で「年式」の係数が有効であると考えられなかったものとしましょう。その場合、「年式」を説明変数から除外した回帰式により予測を行いたくなります。しかし、この検定結果を説明変数の選択に使うことはできません。この段階では「年式」が、あまり予測には役に立っていないということが分かっただけです（「有効でないと分かった」ことも立派な研究成果です）。最初に設定したモデルの妥当性を検討するのには使えますが、モデルそのものを変えてしまうのは本末転倒である、というわけです。

　もちろん、この結果を念頭に置いて、新たにモデルを立て（説明変数を設定し直し）、サンプルを取り直して分析を行うことは問題ありません……というよりは、それが適切な次のステップです。なお、モデルの選択には幾つかの手法がありますが、ベイズ統計によるモデルの比較が扱いやすく、また、分析も柔軟にできます。その方法については、この連載の次に予定しているベイズ統計編で取り上げる予定です（まだまだ先の予定ですが、楽しみにお待ちください）。

説明変数が多い場合や多重共線性がある場合には有意になりにくい

　説明変数の取り方によっても適切な結果が得られないことがあります。説明変数が多くなると、自由度が小さくなるので、結果としてP値が大きくなり、有意になりにくくなります（標準誤差の計算方法を追いかけないと、そのことは分かりませんが、実際にそうなります）。加えて、説明変数同士に多重共線性がある場合（似たような変数を使っている場合）にも、実際には係数が有効であっても、有意になりにくいという性質があります。つまり、あまり意味のない説明変数を加えても、適切な結果が得られないというわけです。

　多重共線性があるかどうかについては、相関行列を作成して、その逆行列を求めることによって調べられます。逆行列の対角成分が5～10を超えると多重共線性が疑われます。計算方法については、こちらでも解説しましたが、念のためサンプルファイルの［多重共線性］ワークシートに計算例と手順を含めておきます。

　この例では、年式が古くなれば走行距離も大きくなると思われるので（排気量はいずれにも関係しないと思われます）、年式と走行距離に多重共線性が現れるかもしれません。が、サンプルファイルでの計算では多重共線性はないと考えられるので、そのまま、それらを説明変数として使っています。

　多重共線性が見られる場合は、似たような説明変数を除外したり、主成分分析によって次元（説明変数）を削減したりしてから、重回帰分析を行うといいでしょう。ただし、次元削減を行うと、説明変数の意味が分かりにくくなります。なお、手順としては、検定結果を見てから説明変数を選択し直すのではなく、適切に説明変数を選択してから検定を行うのが、正しい方法です。有意差を出すことを目的として小細工するのはよくないことだというわけです。

回帰式の係数の有効性を検定する際の適切なサンプルサイズは？

　回帰式の係数の有効性についての検定を行う場合は、一般に、回帰式の当てはまりの良さの検定よりも多くのサンプルサイズが必要になります。関心のある係数のうち、最も効果量が小さい（＝必要なサンプルサイズが多くなると考えられる）ものについて求めたサンプルサイズを採用するのが一般的です。具体的には、こちらに掲載したPythonのプログラムやG*Power（後述）を利用すれば簡単に計算できます。

　上記のリンクからPythonのプログラムを表示し、最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してプログラムを実行するとn=63という結果が表示されます。

　サンプルプログラムは、説明変数の個数をk＝3とし、効果量をf²＝0.3と想定して、α＝0.01, 1－β＝0.95で計算した場合の例となっています。効果量は、以下の式で見積もります。

　ρ²_totalは、全体の決定係数、ρ²_excは、対象となる説明変数を除いた場合の決定係数です（決定係数については、サンプルから得られたR²と区別するためにρ²と表記しています）。サンプルプログラムでは、ρ²_total＝0.5、ρ²_exc＝0.35と見積もったので、f²＝(0.5－0.35) / (1－ 0.5) ＝ 0.3としています。

　第6回で紹介したG*Powerを使う場合は、図3のような画面での操作になります。手順は画面の後に箇条書きで記しておきます。

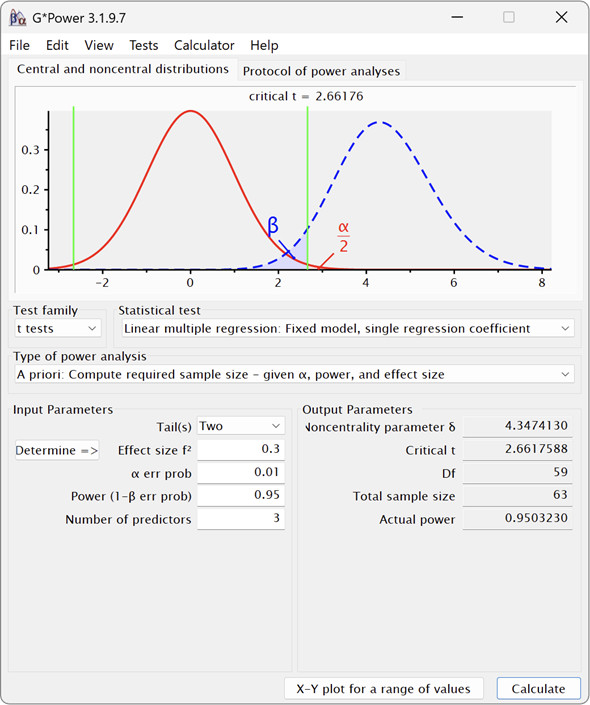図3　G*Powerで係数の有効性についての検定を行う際のサンプルサイズを求める
効果量f²＝0.3、有意水準α＝0.01、検出力1－β＝0.95、説明変数の個数k＝3の場合の例。必要なサンプルサイズは63となる。

　G*Powerでの操作手順は以下の通りです。検定の方法などを以下のように選択します。

［Test family］のリストから「t tests」を選択する
［Statistical test］のリストから「Linear multiple regression: Fixed model, single regression coefficient」を選択する
［Type of power analysis］のリストから「Compute required sample size - given α, power, and effect size」を選択する

　メニューバーから［Tests］－［Correlation and regression］-［Linear multiple regression: Fixed model, single regression coefficient］を選択しても同じ設定になります。

　上記の指定ができたら、以下のように操作します。