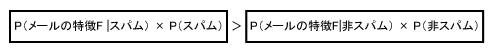綱引きに蛇口当てゲーム？！ 楽しく学ぶベイズフィルターの仕組み：スパム対策の基本技術解説（3/4 ページ）

[草場英仁, 久保山哲二（監修），三井物産セキュアディレクション株式会社／UTCCR情報セキュリティコミュニティ]

ベイズフィルターをもっと詳しく

　基本理論を説明しましたので、本題であるスパムフィルターの実装について解説します。

スパムの判定

　スパム判定のためには、届いた特徴Fのメールがスパムである確率と、非スパムである確率のどちらが大きいかという大小比較ができれば十分です。すると、P（スパム|メールの特徴F）とP（非スパム|メールの特徴F）との大小関係を比較するためには、両者の右辺の分母に共通のP（メールの特徴F）は計算せずに、分子の大きさを比較するだけで十分です。

　つまり、

が計算できれば、特徴Fを持つメールはスパムらしいかどうかが分かるというわけです。

スパムフィルター実装上での問題

　ここで問題です。P（メールの特徴F|スパム）とP（スパム）を計算することは、直接P（スパム|メールの特徴F）を計算するより現実的なのでしょうか。

　まずP（スパム）について考えていきましょう。

　P（スパム）は事前確率です。例えば、いままでに手元に届いたメール中で、スパムと判断したものの割合で計算することができますね。一方で、ベイズ流のスパムフィルターが広く使われるきっかけとなったポール・グレアム（Paul Graham）のスパムフィルターでは、事前に何の知識もないと仮定して、P（スパム）＝P（非スパム）＝0.5としています。

　残るP（メールの特徴Ｆ|スパム）の計算は、現実的なのでしょうか？ 残念なことに、これは現実的ではありません。

　例えば、先ほどのbag-of-wordsによる文章のモデル化をして、メールに現れる単語を特徴Fとします。すると、あるメールに含まれているおのおのの単語wiから、P（メールの特徴F|スパム） = P（w1,w2,……,wn |スパム）を求めなくてはなりません。

　つまり、スパム中で単語w1,w2,……,wn が同時に現れる確率を求めることになります。あらゆる単語の組み合わせについて、このような確率を求めることは、やはり現実的ではないのです。

　そこで、P（w1,w2,……,wn |スパム）の計算のために、さらに大胆な単純化を試みたものが、「単純ベイズ法」と呼ばれる手法です。

　単純ベイズ法では、文章中の単語が、互いに関連性を持たずに独立に現れるという思い切った単純化を行います。例えば、「日時」「場所」といった言葉は、通常強い結び付きを持っていて、「日時」という単語が出てくれば、「場所」という単語が出てくる確率も高くなると考えられます。

　しかし、すべての単語が独立に文章中に現れると仮定することで、このような考慮をした計算を省いてしまうのです。これにより、

　という単純な式で計算できるようになります。

　尤度（ゆうど）であるP（wi|スパム）は、単語wiがスパムに含まれる確率を表しています。単語wiごとにP(wi|スパム) を推定するにはどうすればよいでしょうか。推定する材料が、手元に届いたメールしかないとすると、例えば単語wiが、手元にあるスパムに含まれる割合で計算できそうです。

　しかし、手元にあるスパムには現れていない単語「会議」を含むメールが、スパムとして届いた場合、単純な頻度計算による確率の算定方法では、P（会議|スパム）＝0となってしまい、他にいくらスパムに頻繁に含まれる単語が含まれていたとしても、全体としては、各単語がスパムで出現する確率の積を取っているため、届いたメールがスパムである確率も0と判定されてしまいます。

　このように手元にある限られたメールから尤度（ゆうど）を推定する際に生じる問題を回避するためにさまざまなな手法（スムージング）が提案されています。スムージングの手法については後編で説明しましょう。