データ量を操る圧縮／展開を究めよう：コーディングに役立つ！ アルゴリズムの基本（8）（3/5 ページ）

[山下寛人，オイシックス株式会社]

BitArrayクラス

　ハフマン符号では圧縮データをビット列として保持します。そのビット列を表すBitArrayクラスを作ります。先のソースコードの「末尾1」のコメントの下に以下のコードを追加してください。

<script type="text/javascript">
function BitArray() { this.length = 0; }
 
BitArray.prototype.get = function(begin, len) {
  if(this.length < (begin+len)) { return null; }
  var value = 0;
  for (var i = 0; i < len; i++) {
    value = value << 1;
    value += (this[begin+i] ? 1 : 0);
  }
 
  return value;
}
 
BitArray.prototype.add = function(value, len) {
  for (var i = 0; i < len; i++) {
    var v = value >>> (len-i-1);
    var bit = ((v & 1) == 1);
    this[this.length] = bit;
    this.length++;
  }
}
 
BitArray.prototype.byte_size = function() {
  var size = Math.floor(this.length/8);value="RunLength">
  if ((this.length % 8) != 0) { size++; }
  return size;
}
</script><!-- 末尾2 -->

　コードを解説します。BitArrayクラスは配列の各要素に「0」と「1」のバイナリデータが格納されるものになっています。

4〜13行目

ビット列から数値を取得するメソッドです。ビットの位置beginから長さlenを対象に、ビット列を2進数と見なして数値に変換して返します。

15〜22行目

ビット列に値を追加するメソッドです。valueを2進数に変換し、全体としてlen分のビットをビット列に追加します。

24〜28行目

ビット列のバイトサイズを返すメソッドです。ビット列が配列に入っている状態では実際の内部データ量はより大きくなっていると考えられますが、純粋なバイナリデータになった場合に何バイトになるか計算して返します。

ハフマン符号

　それでは圧縮アルゴリズムに戻ります。予告したとおり、ハフマン符号という手法を紹介します。ハフマン符号は次のような手順でデータを変換することで圧縮します。

• それぞれの文字（データ）ごとに出現回数を調べる
• 出現回数の多い順に並べる
• それぞれの文字に対応するビットデータを作成する
• ビットデータは出現回数が多いものほど、少ないビット数になるようにする
• 元の文字列を、それぞれの文字に対応するビットデータに置き換えていく

　このように、出現回数が多いデータほど少ないデータ量に変換されるので全体として圧縮されます。特に英文では一般的に「a」「e」「t」などの文字は出現頻度が高いので有効です。

　例えば、「abaadacbbc」というデータであれば、各文字の出現回数は以下のようになります。

	文字	出現回数
	a	4
	b	3
	c	2
	d	1

　それぞれに以下のようにビットデータを割り当てます。

	文字	出現回数	ビットデータ
	a	4	1
	b	3	00
	c	2	010
	d	1	011

　これに基づきデータを変換すると次のようになります。

1001101110100000010

　元のデータは、1文字1バイト＝8ビットとすると10文字なので80ビットでした。変換後のビットデータでは、19ビットとデータ量が減っています（ただし、実際には変換表のデータも変換後のデータに含まないといけないので、データ量はもう少し増えます）。

ビットデータの作成

　では、ビットデータの作成はどのようにしたらよいでしょうか。それは、木構造を作ることで作成できます。

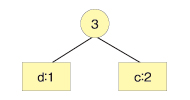
　出現回数が少ないものから2つ取り出し、2分木のノードを作ります。出現回数が多い方を右にします。ノード自体にも出現回数のデータを持ちます。これは両方の出現回数を合計したものにします。

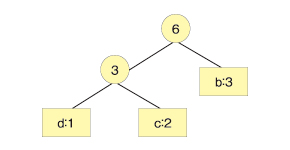
　このひとまとまりのノードと、次に出現頻度が少ない文字を取り出し、2分木のノードを作ります。

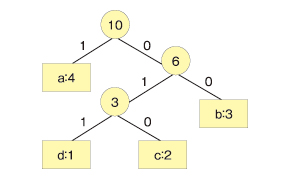
　同様に木構造の上部にノードを作り、文字を追加していきます。木の左に「1」のビット、右に「0」のビットを割り当てます。

　木のルートから各文字までをたどっていきます。それぞれのパス上のビットを上から組み合わせたものが各文字に対応するビットデータになります。例えば、cならルートから右→左→右なので、「010」となります。