Rで実践する統計的検定の初歩：実践！ Rで学ぶ統計解析の基礎（2）（2/3 ページ）

[柏野雄太，バクフー株式会社]

有意水準、p値

　一般に、確率密度分布が分かっている確率変数がある場合、その確率変数に範囲を与えれば、その範囲の積分することにより確率を求めることができます。

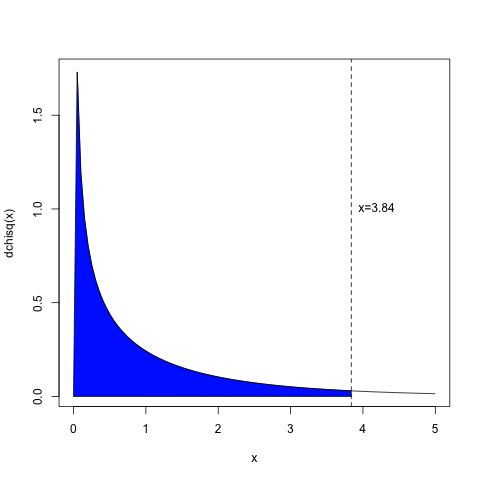
　例えば自由度1のカイ二乗分布の場合、定義域が0から3.84までの値、つまり以下の図の0から破線までの範囲を積分すると、その値は青い領域になり、約0.95、つまり確率は約95％になります。

　このことは、確率密度がカイ二乗分布を持つ確率変数を考えたときに、無作為に選んだその確率変数の値がx=0からx=3.84の間に含まれる確率は、約95％になると言い換えることができます。これはカイ二乗密度分布から確率を計算するRの組み込み関数pchisqで以下のように計算ができます。

> pchisq(3.84, 1)
[1] 0.9499565

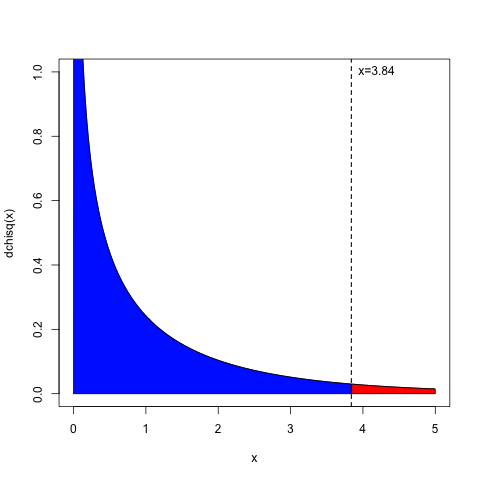
　このことを逆に考えますと、確率密度がカイ二乗分布を持つ確率変数を考えたときに、無作為に選んだその確率変数の値がx=0からx=3.84の間に含まれない確率は、全確率から0.95を引いた値、「1-0.95 = 0.05」、つまり約5％残っているということです。その領域を図で示すと、以下の図の赤の部分です。

　Rで計算するには、全確率1からpchisqを引きます。

> 1-pchisq(3.84, 1)
[1] 0.05004352

　統計的検定をする確率変数は、帰無仮説を元に計算した統計量です。いま考えている例は、観測した分布と期待している分布の類似の程度を表わすx²でした。この帰無仮説を元に計算した統計量と、無作為に選んだ確率変数が存在する「ある確率水準」を比べることが、統計的検定では決定的に重要になります。この判定の基準となる「ある確率水準」を全確率1から引いたものを有意水準と呼びます。

　有意水準は、統計的検定を行う分野で使われている基準がなければ、5％や1％を慣習的として採用する場合が多いようです。上記の例では5％有意水準をとった図を描いたことになります。つまり、無作為に選んだ確率変数が青の領域にいる確率は95％ですが、赤の領域にいる確率は5％ということです。そして、帰無仮説を元に計算した統計量が有意水準にいる、つまり赤の領域にいるかどうかというので、統計的検定を行います。赤の領域というのは、無作為で選んだ確率変数が存在する確率が5％（や1％などの）有意水準であり、なかなか状況として起こりにくいということです。帰無仮説を元に計算した統計量がこの赤の領域に入るということは、その統計量は実現しにくい、すなわち帰無仮説を支持することが難しいということになります。

　もう一度定理に戻ります。カイ二乗適合度の定理は、観測から求めることができる確率変数x²が、十分に観測のサンプル数が大きい場合にカイ二乗分布と近似できるというものでした。そして、このx²という値は、観測した分布と期待している分布の類似の程度のようなものでした。その類似の程度が赤の領域にあるということは、その類似の程度は確率的に起こるのが難しいということになり、観測した分布と期待している分布が同じとはいえない、ことが言えます。

　そこで実務者としてやるべきことは、観測した分布と期待している分布の類似の程度を表すx²の値を計算し、それが自由度k-1のカイ二乗分布のどの位置に該当するか調べ、その位置が有意水準に含まれるかどうかを見ればいいわけです。

　ここでは、この一連の手順をchisq.test関数を使うのではなく、実際にx²の値を計算することで原理を明らかにします。では計算してみましょう。

> jcount <- data.jleagers
> xsq <- sum((jcount-sum(jcount)*prob)^2/(sum(jcount)*prob))
> xsq
[1] 89.56353

　jcountにはJリーガーの月別出生数が入っていて、probには日本人の月別出生比率（母比率といいます）が入っています。sum(jcount)*probは月別出生数の期待度数を計算しているところです。さて、このxsqがカイ二乗分布においてどの程度の確率を占めるかを調べるには、pchisqを利用します。そして、この場合のカイ二乗分布の自由度とは、月数12から1を引いた11になります。これは、カイ二乗分布の自由度は一様分布を仮定するとき、定理にあるように、カテゴリ数をkとしてときにk-1になるからです（ここで実は、若干の不整合があります。前回書きましたように、実は日本人の月別出生分布は正確には一様分布でありません。従って、本当は自由度を別途計算しなければなりません。しかし、この値は影響範囲が小さいのでこのまま近似的に成り立つとします）。

> 1-pchisq(xsq,11)
[1] 2.031708e-14

　この値を統計量x²のp値といいます。この値はchisq.testのp-valueと同じ結果であることがわかります。p値の計算式を見ると分かるように、これは検定するべき統計量が取る値およびそれ以上の値を取る確率を表しています。p値は帰無仮説が正しいとして、検定するべき統計量の値と、それより起こりそうもない値がどれだけの割合で出現するかを示すものです。p値を利用すれば、有意水準と直接比較することができます。ですから、前回はp-valueの値をみて、すぐに帰無仮説が棄却できるかどうかを判断したのです。

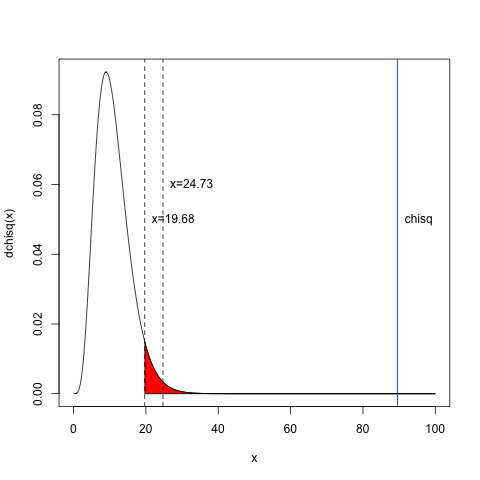
　以上の状況を図示すると次のようになります。

　グラフは自由度11のカイ二乗確率密度関数で、x=19.68の破線が有意水準5％, x=24.73の破線が有意水準1％の線をあらわします。赤の領域が有意水準5％より小さな領域で、帰無仮説を元に計算されたx²の位置を表すのが青い実線です。これを見ると分かりますように、有意水準5％や1％よりも、はるかに右に位置しています。

　そのために、x²値が実現する可能性は著しく低い、すなわち帰無仮説である「Jリーガーの月別出生数分布は日本人の月別出生数分布と同じである」という言明は棄却できることになります。

統計的検定ということ

　いままでやってきた、適合度のカイ二乗検定をまとめると、以下のとおりです。

• 有意水準を設定する
• 帰無仮説を立てる。帰無仮説は本来示したいことの反対の言明
• 帰無仮説が正しいとして、そのときの統計量x²を計算する
• x²のp値は有意水準より小さいか？ つまり、帰無仮説を元にしたx²は起こりにくい値か？
• p値が有意水準より小さい場合：帰無仮説を棄却する
• p値が有意水準より大きい場合：帰無仮説は棄却できない

　ここで注意することは、帰無仮説が棄却できない場合、帰無仮説が正しいとするのは、正確には間違いだということです。そうではなく、帰無仮説を正しいとするにはデータが十分でない、と控えめに言わなければなりません。そもそも、本来示したい言明ではなく、その反対の言明である帰無仮説を立てて、帰無仮説を反証するというやり方も、日常的な感覚からすると、かなりひねくれたやり方でしょう。

　これは統計的検定の検証方法全体に関係しています。基本的な姿勢として、何らかの言明というのは反証するのは可能だが、検証するのは極めて困難である、という科学の認識論に根ざしています。これは、科学哲学者のカール・ポパーが「反証可能性を持つ理論のみが科学的理論である」と科学を規定し、科学理論は決して証明することはできないが、反証できるか、もしくは反証を失敗し続けることができる、としたことに非常に似ています。

カール・ポパー著、藤本隆志＝石垣寿郎＝森博訳『推測と反駁?科学的知識の発展』法政大学出版局、1980年