Rで実践する統計的検定の初歩：実践！ Rで学ぶ統計解析の基礎（2）（3/3 ページ）

» 2010年08月04日 00時00分公開

[柏野雄太，バクフー株式会社]

統計的検定に対するいくつかの批判

　さて、上記のように手順としてまとめてしまうと、機械的に統計的検定が行えるかのような錯覚を覚えます。事実、Rのような統計計算環境を持っていれば、データを与えてパラメータを設定するだけで、結果を得られます。

　しかし、近年は統計的検定の濫用を戒める論調が強くなっているのが現実です。これにはいくつか論点があるのですが、例えば統計的検定には次のような不都合があるという指摘があります。

　まず、データ数が多いと、帰無仮説を棄却しやすくなります。つまり、自分が示したい言明を採用したいたがめに、無闇にデータを集めるというインセンティブができてしまいます。本来、物理学や化学などの実験と関係する科学では、データが集まり観測精度・測定精度が高くなるにつれ、検証しようとする理論が反証されやすくなるものです。しかし、統計的検定で反証するのは自分が示したい言明とは逆の帰無仮説なので、ちょうど反証するべき方向が通常の実験科学と逆向きなのです。このことは、統計を道具として使うときに、悪いインセンティブを与えるという批判があります。これに対して、ベイズ的な統計手法を利用すれば、この問題を回避しやすいとする意見もあります。

　次に、意味のないランダムデータに関して統計的検定を利用しても、有意な結果を得られるとする研究があります。このことは統計的検定の結果が出たからといって、それを絶対視することができない、ということです。

Freedmann, D. A. 1983 "A note on screening regression equation.", The American Statistician, 37(2):152

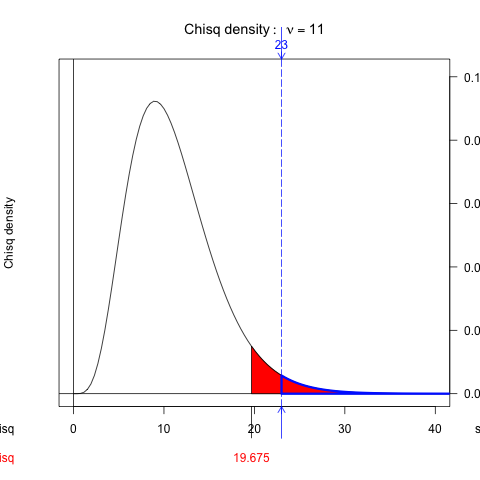
　さらに、統計的検定はp値で判定すると上で述べましたが、このp値は「検定するべき統計量が取る値、およびそれより起こりにくい値を取る確率」です。このことをもう少し詳しく説明します。例えば、先程の例のように自由度11のカイ二乗分布で、有意水準を10％とするカイ二乗検定を行うとします。この状況を以下の図に示しました。

　有意水準を10％に相当するカイ二乗値は19.675になります。図では全確率の10％に相当する面積が赤で塗られています。いま、検定するべき統計量がx=23であったとします。図では青の破線で書かれた部分です。青い実線で囲まれた領域はx=23のときのp値です。検定というのは、有意水準とp値による比較、つまり図の赤で囲まれた領域と、青い実線で囲まれた領域を比べて、この大小で帰無仮説を棄却するか否かを決めます。赤い領域に比べて青い領域が小さければ、帰無仮説が棄却される、ということです。

　ここで、青の領域というのをよく考えてみると、青い領域には検定統計量であるx=23とそれより大きい（確率として起こりにくい）xの無限大の値までが対象になっています。つまり、「検定するべき統計量がとる値」だけでなく、観測されるとは限らない「それより起こりにくい値」というものが、検定の過程でコッソリ導入されているのです。そして、こういう操作をしても問題ないのか？という批判が、統計的検定には常にあります。

Johnson, Douglas H. 1999 "The Insignificance of Statistical Significance Testing", Journal of Wildlife Management 63(3):753

　その他、統計的検定にはいろいろな批判がありますが、筆者が深く共感するのは、北海道大学の久保拓弥さんの次の主張です。

　久保さんは、計算機環境が充実したこの時代に簡便的計算方法である統計的検定にこだわる必要がないとし、統計モデルを構築し、その選択を行う手法を利用すれば、より精緻な議論ができると言います（久保拓弥「検定とモデル選択」）。

　以上、統計的検定に対する批判を概観しましたが、それでもやはり統計的検定は便利なツールであるのは間違いありません。使い方を誤用・濫用しなければ、使い続けるのになんら支障はないと思います。

　さて、統計的検定をキチンと議論するには、その他にも「タイプ1、タイプ2のエラー」や「検出力」そして「サンプルのバイアス」について、さらに説明しなければなりません。しかし、これらの説明は長大になってしまいますし、本連載で試みようとしている実践的な内容から大幅に外れて、道具を使う姿勢のような訓詁（くんこ）学的な話になっています。そこで、ここで一旦手を動かす話題に戻り、統計的検定を練習する方向に戻してみたいと思います。

二項検定を適用してみる

　Rにどれだけ統計的検定関数があるのかを調べるには以下のようにapropos関数を利用すれば、おおよその統計的検定関数を列挙することができます。

> apropos(".test")
 [1] ".valueClassTest"      "ansari.test"          "bartlett.test"       
 [4] "binom.test"           "Box.test"             "chisq.test"          
 [7] "cor.test"             "file_test"            "fisher.test"         
[10] "fligner.test"         "friedman.test"        "kruskal.test"        
[13] "ks.test"              "mantelhaen.test"      "mauchley.test"       
[16] "mauchly.test"         "mcnemar.test"         "mood.test"           
[19] "oneway.test"          "pairwise.prop.test"   "pairwise.t.test"     
[22] "pairwise.wilcox.test" "poisson.test"         "power.anova.test"    
[25] "power.prop.test"      "power.t.test"         "PP.test"             
[28] "prop.test"            "prop.trend.test"      "quade.test"          
[31] "shapiro.test"         "t.test"               "var.test"            
[34] "wilcox.test"

　組み込みだけでもかなりの関数があることが分かります。これ以外にパッケージとして提供されているもの（http://cran.r-project.org/web/packages/）を含めると、数えるのが困難なほどの検定関数が実装されています。

　この中で一番簡単な二項検定関数を用いて統計的検定の練習をしましょう。具体的にはbinom.test関数を、Jリーガーの月別出生分布に適用したいと思います。検定したい帰無仮説は「4月生まれのJリーガーの人数（比）は、ランダムに選ばれた集団の人数（比）と変わらない」です。

　ここで二項分布について簡単に説明しておきましょう。まず、ある事象が起こるか起こらないかだけを記録する繰り返し型の実験を考えます。事象がおきる確率をpとすると、起こらない確率qは「q = 1 - p」になります。試行をn回繰り返したとき、その分布は以下の二項分布に従います。

　この式の導出はどんな初歩的な統計学の本にも載っていますので、ここでは割愛します（先ほどのホエールの本でもp58に載っています）。二項分布は起こるか起こらないかという事象を説明するときに使うということ、統計分布が明らかなのでp値を計算することができ、統計的検定に利用できる、ということが分かればいまは十分です。

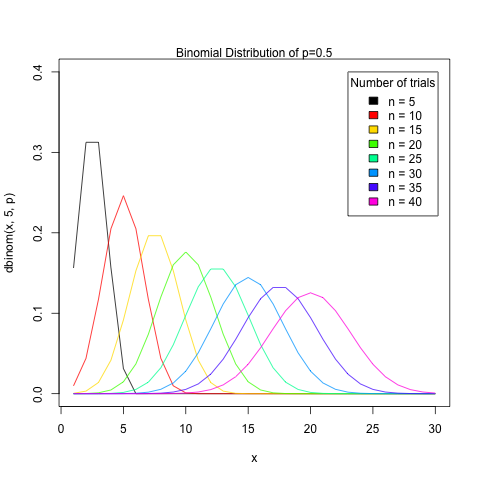
　例えば、p=0.5として試行回数nを動かしたときの二項分布のグラフは以下のようになります。

　今回の例の場合、4月生まれというのが成功する事象で、それ以外が失敗の事象です。ランダムで選ばれた集団では人は12月に均等に配分されるはずですから、確率はp = 1/12です。実験の回数nはJリーガーの人数そのものです。これをbinom.test関数に適用します。第1引数に4月生まれの人数、第2引数にJリーガーの人数、そして先ほどの確率1/12を入れた結果が以下のとおりです。binom.testの仕様を詳しくは知るには、help("binom.test")によって、ヘルプを参照ください。

> binom.test(jcount[4], sum(jcount), p=1/12)
	Exact binomial test
data:  jcount[4] and sum(jcount) 
number of successes = 125, number of trials = 1073, p-value = 0.0001678
alternative hypothesis: true probability of success is not equal to 0.08333333 
95 percent confidence interval:
 0.09790618 0.13721717 
sample estimates:
probability of success 
             0.1164958

　これを見ると分かるように、p-value = 0.0001678というp値が小さな値をとるので、「4月生まれのJリーガーの人数（比）は、ランダムに選ばれた集団の人数（比）と変わらない」という帰無仮説は棄却できそうです。

　さらに、同じように「4月生まれのJリーガーの人数（比）は、4月生まれの日本人集団の人数（比）と変わらない」という帰無仮説を検証したいと思います。それには、さきほどの確率部分に日本人集団の4月生まれの確率（母比率）p = prob[4]を用います。

> binom.test(jcount[4], sum(jcount), p=prob[4])
	Exact binomial test
data:  jcount[4] and sum(jcount) 
number of successes = 125, number of trials = 1073, p-value = 9.243e-05
alternative hypothesis: true probability of success is not equal to 0.08194434 
95 percent confidence interval:
 0.09790618 0.13721717 
sample estimates:
probability of success 
             0.1164958

　こちらもp-value = 9.243e-05というp値が小さな値をとるので、「4月生まれのJリーガーの人数（比）は、4月生まれの日本人集団の人数（比）と変わらない」という帰無仮説は棄却できそうです。

　以上を見ると分かるように、カイ二乗検定でも二項検定でもJリーガーの出生月は、ランダムに選ばれているわけでも、日本人集団と同じわけでもなさそうだということが定量的に示せました。これが「マタイ効果」によるものかどうかは、この段階では分かりません。ただし、Jリーガーの出生月分布が日本人集団と離れていることは示せましたので、「マタイ効果」は十分検証する価値がある問題だ、ということは言えそうです。

タコのパウルによる予想

　さて、もう少しだけ手習いを続けましょう。またもやサッカーの話題になります。今年のワールドカップサッカーでは、ドイツ・オーバーハウゼンの水族館シー・ライフで飼育されているマダコ、パウル（パオル）によるサッカー予想がとても話題になりました。Wkipediaによるパウルの予想は、以下のとおりです。


対戦国	大会	ステージ	予言	試合結果	正誤
ポーランド	EURO2008	グループステージ	ドイツ	2-0	正
クロアチア	EURO2008	グループステージ	ドイツ[13]	1-2	誤
オーストリア	EURO2008	グループステージ	ドイツ	1-0	正
ポルトガル	EURO2008	準々決勝	ドイツ	3-2	正
トルコ	EURO2008	準決勝	ドイツ	3-2	正
スペイン	EURO2008	決勝	ドイツ	0-1	誤
オーストラリア	WC2010	グループステージ	ドイツ	4-0	正
セルビア	WC2010	グループステージ	セルビア	0-1	正
ガーナ	WC2010	グループステージ	ドイツ	1-0	正
イングランド	WC2010	決勝トーナメント1回戦	ドイツ	4-1	正
アルゼンチン	WC2010	準々決勝	ドイツ	4-0	正
スペイン	WC2010	準決勝	スペイン	0-1	正
ウルグアイ	WC2010	3位決定戦	ドイツ	3-2	正
オランダ対スペイン	WC2010	決勝戦	スペイン	0-1	正
パウルのサッカー予想と、その結果

　さて、いま「パウルの食餌行動がサッカー予想と結びついている」という仮説を暗黙の仮定として置いた上で、このパウルの「戦績」について定量的に検証しましょう。

　まず、パウルのEuro2008とワールドカップ2010を合わせた予想成績は14勝、12敗だそうです。「パウルの予想は偶然である」という帰無仮説を立てて、二項検定で検証したものが以下のものです。

> binom.test(12, 14, p=0.5)
	Exact binomial test
data:  12 and 14 
number of successes = 12, number of trials = 14, p-value = 0.01294
alternative hypothesis: true probability of success is not equal to 0.5 
95 percent confidence interval:
 0.5718708 0.9822055 
sample estimates:
probability of success 
             0.8571429

　p-value = 0.01294となりました。これは有意水準1％では帰無仮説を棄却できませんが、5％では棄却できます。つまり、有意水準5％ではパウルの予想は偶然ではない可能性が高いということです。

　さらに、ワールドカップだけに限定しますと、8試合中8つというように、パウルは完全に予想を当てました。これを「バウルの予想は偶然である」という帰無仮説を立てて、二項検定で検証してみましょう。

> binom.test(8,8, p=0.5)
	Exact binomial test
data:  8 and 8 
number of successes = 8, number of trials = 8, p-value = 0.007812
alternative hypothesis: true probability of success is not equal to 0.5 
95 percent confidence interval:
 0.6305834 1.0000000 
sample estimates:
probability of success

　p-value = 0.007812となりました。これは有意水準1％であっても、「パウルの予想は偶然である」という帰無仮説は棄却できる、つまりパウルの予想は、まぐれでない可能性が高いということです。

　これを見ますと、確かにこのパウルの事例については驚くべき結果とも言えなくはないですが、そもそもの問題として「パウルの食餌行動がサッカー予想と結びついている」という仮説が正しいと証明できない限り、これはあくまで飲み屋ネタにしかならないでしょう。

次回について

　今回はRを用いて統計的検定の初歩を実践しました。統計的検定の大雑把な概念説明とそれに対する批判にも言及しました。Jリーガーの誕生月とパウルの予想についての話題をとりあげ、適合度のカイ二乗検定と二項検定についてRを利用して実践しました。次回は第1回、第2回にガッツリしたネタを持って来すぎたかもしれない、ということを反省し、少し軽めの話題にしようと思います。オープンデータを利用してRでグラフを描いて可視化するだけでも、いろいろな知見が得られる、というのをテーマにしようかと思います。それでは、2週間後にまたお目にかかりましょう！

「次回」へ

「実践！ Rで学ぶ統計解析の基礎」バックナンバー