自動車を制御するロボットの思考と行動の仕組み――Google Carが現実世界を認識する際の3つのアルゴリズムと実用化への課題:Google Carの自動運転技術大解剖(2)(2/3 ページ)
Google Carにおける解決方法――確率ロボティクス
Google Carは、このようなロボット制御の問題に対し、「Probabilistic Robotics」(確率ロボティクス)という研究分野の手法を用いて解決を図っています。実はGoogle Carを生み出したSebastian Thrun氏は、この研究分野の第一人者であり、この分野では有名な書籍『確率ロボティクス』(毎日コミュニケーションズ刊)を執筆しています。Google Carは、このProbabilistic Roboticsの集大成と言っても過言ではありません。
書籍の前にUdacityが理解の近道かも
書籍『確率ロボティクス』はGoogle Carのような自動運転を実現しようとした際には、必ず目を通す必要がある書籍でしょう。
また、Udacityで筆者が受講した内容も、実はこの「Probabilistic Robotics」の書籍の内容をベースにした講義でした。もしも「この書籍を読み解こう」という人が居るならば、書籍を読み解く前に、UdacityにおけるThrun氏の講義を受講することが理解の近道になります。
さて、Probabilistic Roboticsの「Probabilistic」とは「確率」のことです。Probabilistic Roboticsでは、現実世界と仮想世界をつなぐ部分に必ず発生する不確実性に対し、確率(正確には「ベイズ確率」)で対処します。
【1】状況の把握
例えば、ロボットが地図上のどこに存在するかを特定したいとします。このようなタスクを「ローカライゼーション(localization)」と呼びます。分かりやすさのために、ここでは2次元や3次元の地図を用いず、ロボットはx座標のみの1次元空間上のどこかに存在するとします。つまり、ここでの想定は、ロボットの制御コンピューターの内部で持つ仮想世界は1次元ということになります。
「直線上の、どこにロボットが存在するか」を決めるために、最初のセンサーの読み取りを用います。ただし、センサーには測定誤差があるため、完全に信用することはできません。ロボットが内部で持つ仮想世界の表現を考えた際、ピタッと「この地点にロボットが居る」とは断言できないのです。この問題を解決するため、Probabilistic Roboticsでは「だいたい、この辺りにロボットが居る確率が高い」という表現をします。つまり、居場所の断定はせず、センサーの読み取り誤差も考慮に入れた、ある意味あやふやな「存在確率」として位置情報を表現するのです。
具体的には、「この辺りに居る確率が高い」という情報を確率分布として捉えます。この確率分布はセンサーで測定した位置を山頂とし、周囲になだらかに裾野が伸びたような山状の確率分布となるでしょう。
また、複数のセンサーがそれぞれ別の位置を指し示すこともありますが、この場合はその結果をマージし、複数の山があるような確率分布となります。センサーの読み取り結果は大抵バラバラですから、複数の山ができる方が自然でしょう。「確率分布の山が複数ある場合、実際に車が存在する場所は最も山が高い場所である」と考えます。
【2】行動計画の立案→【3】計画した動作を実行
さて、ロボットが行動計画を立案し、「右に1m車を動かすことにした」としましょう。そして、ロボットの持つ仮想世界の中でも右に1m車を動かし、「ロボットがどのような状況になっているはずか」を物理シミュレーションの結果として保持したいとします。
この際、単純に考えると上記の確率分布を1m分右方向にスライドすればロボットの持つ仮想世界の中でもきちんと右方向に動かしたことになると思いたいのですが、ここでもう一つ考えておくべきことがあります。それは、「実際に車がちゃんと1mほど右に動くとは限らない」ということです。
制御誤差は常に発生します。制御の結果、実際には移動量が1mに満たなかったり1mをオーバーしてしまったりすることは頻繁に発生します。そのため、確率分布は右に単に1mスライドするだけではなく、確率分布の山を若干低くし、また、山の裾野を若干広くしたような確率分布とする必要があります。
これは要するに、「あまり自分の位置に自信のない確率分布」ということです。このことを人間に当てはめて考えると、「ある場所に立って目を閉じ、目を閉じたまま歩く」ことを考えてみると分かりやすいです。
最初は自分の位置は明確に分かっているでしょう。しかし、目を閉じて歩いているうちに、自分がどこに居るのか急速に分からなくなっていきます。ただ、分からないなりに「この辺りに居るはず」というイメージはあり、その「この辺り」という範囲が目を閉じて歩いている間にどんどん広がり、自信もなくなっていきます。これと同じことを「確率分布」という表現方法で示したのが、下図です。
2回目以降の「状況の把握」
ここまでで、ロボットの制御サイクルが1サイクル回りました。次のサイクルでは再度周囲の状況を把握するためにセンサーの読み取りを行います。この際、初回のセンサーの読み取りでは使えなかった情報が使えるようになっています。それは前回のロボットの制御サイクルの最後で更新しておいたロボット内部で持っている仮想世界の情報です。この仮想世界では、自信がないなりに「自分はこの辺りに居るはず」という情報が残っています。この情報が2度目以降の制御サイクルで利用可能なのです。
前回の制御サイクルの最後で得られる仮想世界から来る確率分布も、新たなセンサー情報から来る確率分布も、どちらも不確かな情報で、それぞれ単独の情報のままでは確実な情報は得られません。しかし、この両者を重ね合わせると、より確かな確率分布を得ることができるのです。
これは直観的に理解できるものです。というのも、ロボットが「自分はこの辺りに居るはず」と思っていることに対し、センサー情報を使ってより正確な位置となるように補正を加えることになるためです。2つの確率分布を個別に利用するよりも、2つの確率分布の合成結果の方が、精度が高くなりそうだと直観的に思えるのではないでしょうか。
さらに、ロボットはこのような位置推定を短時間に何度も行います。センサーによる測定を何度も繰り返し行い、その測定結果は制御サイクルをまたいで引き継がれていきますので、どんどん正確性は増していきます。このようなロボットの位置推定の考え方を「Markov Localization」と呼びます。
関連記事
 第166回 AppleかGoogleか? クルマのIT化が次なる戦場
第166回 AppleかGoogleか? クルマのIT化が次なる戦場
AppleとGoogleの戦いが自動車市場を舞台に始まった。両社のアプローチは違うものの、クルマのIT化をターゲットにしているのは同じ。さて、スマートフォン市場に続き、自動車市場でも両社の戦いは続くのか? 第162回 クルマの自動運転に求められること
第162回 クルマの自動運転に求められること
自動車の自動運転技術に対する注目が急速に高まっている。自動運転というのは、いわばクルマに自前の目や脳を載せるという技術である。半導体技術が支える面も大きい。そこには、まだいくつかの課題がありそうだ。 「Google Car」が勝つかどうかにかかわらず、自動車産業は変質する
「Google Car」が勝つかどうかにかかわらず、自動車産業は変質する
グーグルが完全な自律走行車の実用化を目指して、開発・検証、ロビー活動を進めているのは周知の事実だ。グーグルといえども既存の自動車メーカーに、従来の意味合いで容易に「勝つ」とは想定しにくい。それでも、既存の自動車メーカーには、「グーグル対策」を自社の将来と重ね合わせて考えなければならない理由がある。 Android L、Android Wear、Android TV、Android Autoの開発者向け現状まとめ
Android L、Android Wear、Android TV、Android Autoの開発者向け現状まとめ
米グーグルが「Google I/O 2014」で発表した次期Android「Android L」「Android TV」「Android Auto」の開発者プレビュー、そして「Android Wear」の正式版。これらに対応したアプリを開発するには、どこを見ればいいのか。概要とともに簡単にまとめてみた。
Copyright © ITmedia, Inc. All Rights Reserved.

 全てのセンサーデータを用い、x座標中のどこにロボットカーが居るのかをさまざまな方法で推定し、それを確率で表現する
全てのセンサーデータを用い、x座標中のどこにロボットカーが居るのかをさまざまな方法で推定し、それを確率で表現する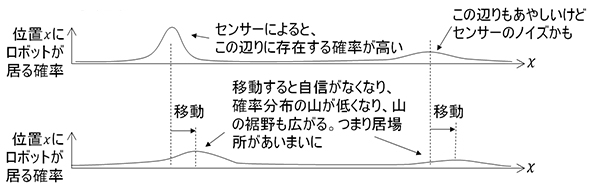 行動計画を立案し、「1」ほど右に車を動かすことにしたとする。しかし、実際に車がちゃんと「1」ほど右に動くとは限らない。上図の確率分布はこのように変化する
行動計画を立案し、「1」ほど右に車を動かすことにしたとする。しかし、実際に車がちゃんと「1」ほど右に動くとは限らない。上図の確率分布はこのように変化する




