グラフデータベースはどんな用途に向いている?:Database Watch(2015年7月版)(1/2 ページ)
関係性を表現するのが得意なNoSQL「グラフデータベース」。通常のリレーショナルデータベースでは複雑になるデータモデルを扱える理由と適用領域などを「Neo4j」を題材に紹介します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
最近耳にすることが多くなった「グラフデータベース」。名前に「グラフ」が付きますが、グラフ描画などとは関係ありません。グラフデータベースとは、「ノード」「リレーション」「プロパティ」の3要素によってノード間の「関係性」を表現する「グラフ型のデータモデル」を持つデータベースといえます。
リレーショナルデータベースではないため「NoSQL」に分類されますが、この「グラフ型のデータモデル」とは、NoSQLといったときに一般的に想起される「KVS(キーバリューストア)型データベース」や「MongoDB」のような「ドキュメント指向データベース」とは異なるデータモデルとなります。
例えば、フェイスブックの「ソーシャルグラフ」を支える「Open Graph」(関連記事)や、「Linked Open Data」で使われる「RDF」の記述(関連記事)などもグラフ型のデータモデルです。このデータモデルを使って、経路やインデックスを構築すれば、ソーシャルネットワークサービス(SNS)に見られる「知り合いかも」というサジェストや、さまざまな制約条件がある複数の経路のうち「最短の経路を探す」といったクエリの答えを得られるというわけです。
主要な商用データベース製品でも、例えばOracle Databaseのオプション「Oracle Spatial and Graph」などでグラフデータベースが利用できるようになっていますが、今回は、オープンソースのグラフデータベース「Neo4j」を題材に、グラフデータベースの特徴を見ていきます。本稿ではクリエーションライン 執行役員でNeo4jに詳しい鈴木逸平氏に話を聞きました。鈴木氏といえば、2年前に「納涼もんご祭り」(MongoDBのイベント)を紹介した記事でも登場いただきました。最近ではMongoDBだけではなく、Neo4jの普及にも力を入れているそうです。
グラフデータベースとは?
インタビューでは、Neo4jの話に入る前に、まず「グラフデータベース」そのものについて聞いてみました。鈴木氏によると、グラフデータベースは「関係性を表現するグラフ」を持つため、複雑なデータの探索に向いているそうです。これだけでは、すぐにイメージがつかめないかもしれませんね。
例えば地下鉄の路線図のような形で、プロパティを持つ交点(ノード)とその間に関係性を表す線(リレーション)が引かれているのが、グラフデータベースにおけるデータモデルのイメージです。人物相関図にも当てはまりますね(路線図そのものはグラフデータではありません)。
フェイスブックやリンクトインのようなソーシャルネットワークサービスでは、既にグラフデータベース技術を活用しています(フェイスブック、リンクトインともグラフデータベースはNeo4jではなく独自開発したものを使っています)。
「AさんとBさんは高校の同級生である」というような「ある時点の人物相関関係」なら二次元の図で表現できそうですが、人間関係は時間によって変化しますし、他の要素や関係性も含めると多次元になってしまいます。こうした複雑なデータモデルにグラフデータベースは適しています。
SNS以外にもグラフデータベースの活用例は広がってきています。例えば、通信ネットワークや電力のグリッド網もグラフデータベースのデータモデルに近いです。
実際にソーラーパネルを使った発電と配電システムの運用管理にも使われており、どこで問題が起きたか判別したり、問題が起きたときに、どこからどこまでのエリアの送電を止めれば被害を最小限に防げるのかを考えたりする場合に使われているそうです。
地図上で最適ルートを調べるのにもグラフデータベースは適しています。配送ルートは配達だけではなく集荷や給油もあり、とても複雑だからです。
これまでの事例をリレーショナルデータベースで構築することは不可能ではありません。しかし、多数の交点からなるデータモデルをリレーショナルデータベースで扱おうとすると、「JOIN」を多用しなくてはなりません。また、スキーマを考えるのも苦労が要りますし、どのように考えても複雑になってしまいます。
その点、グラフデータベースならもともとそうしたデータモデルを想定しているため、直感的に扱うことができます。
column:ケーニヒスベルクの橋問題と一筆書きとグラフデータベース
グラフ型データモデルは「ケーニヒスベルクの橋問題」に源流を見いだすことができます。
ケーニヒスベルクの橋問題は、「奇数本の線が出ている交点が三つ以上ある場合は必ず一筆書きできない」という一筆書きの法則としてよく知られています。
さて、このケーニヒスベルクの橋問題は、18世紀にまで時代をさかのぼります。七つの橋が架かっている町で「それぞれの橋を一度だけ通って全ての橋を渡ることは可能か」という問いが町の皆を悩ませたのです。これを「不可能である」と証明したのが、著名な数学者であるレオンハルト・オイラーです。このケーニヒスベルクの橋問題に対するオイラーの証明が「グラフ理論」の起源といわれています。
最適なルート判定でいうと「中国人郵便配達問題」「巡回セールスマン問題」なども、数学の問題としてよく知られています。これらについても解法が研究されており、グラフデータベースは、こうしたロジックを計算に組み込むことで、シンプルに答えを導きだそうとするものです。
ここでは理論の詳細は割愛しますが、グラフ理論をデータモデルに応用したのがグラフデータであり、それをデータベースとして扱えるようにしたのがグラフデータベースと理解すると良いでしょう。
Copyright © ITmedia, Inc. All Rights Reserved.

 クリエーションライン 執行役員 鈴木逸平氏
クリエーションライン 執行役員 鈴木逸平氏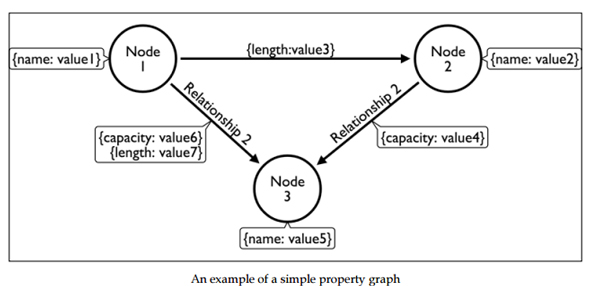 グラフで記述されたデータモデルの例(出典:Rik Van Bruggen『
グラフで記述されたデータモデルの例(出典:Rik Van Bruggen『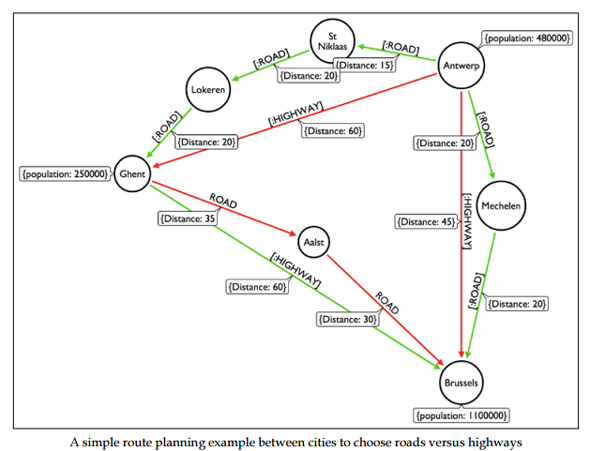 都市間の輸送計画をグラフデータで記述した場合の例(出典:Rik Van Bruggen『
都市間の輸送計画をグラフデータで記述した場合の例(出典:Rik Van Bruggen『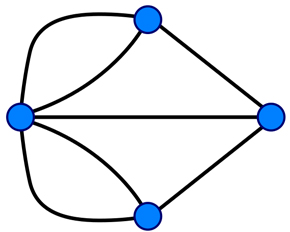 この図は一筆書きができない(出典:Wikipedia日本語版「
この図は一筆書きができない(出典:Wikipedia日本語版「



