二分探索:Dev Basics/Keyword
二分探索は、ソート済みのデータ列の中から特定の要素を探索するアルゴリズム。全ての要素を順に検索する線形探索よりも高速に探索を行える。
二分探索は、ソート済みのデータ列の中から特定の要素を探索するアルゴリズム。全ての要素を順に検索する線形探索よりも高速に探索を行える。
線形探索と2分探索
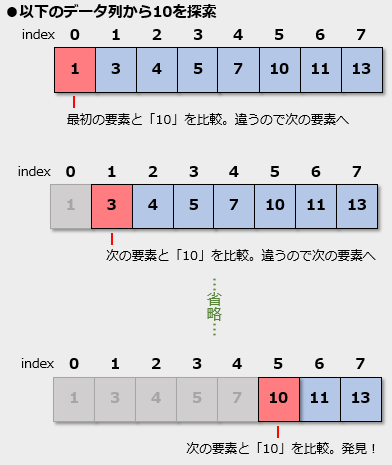
線形探索とは、配列などに格納されているデータを探索(検索)する際に先頭要素から順に探索対象のデータと要素とを比較していくこと。例えば、「1, 3, 4, 5, 7, 10, 11, 13」という整数値を含むデータ列から「10」を探索すると次のようになる。なお、ここでは探索対象の配列はソート済みとする。
線形探索では、探索で行う最大の比較回数は要素数と等しくなる(配列の末尾要素が探索対象である場合)。
これに対して、二分探索では要素を含んだ配列などを2分割していきながら、データの探索を行う。二分探索では、要素数をnとしたとき、探索で行われる比較回数は最大でもlog2n回となる。線形探索においては今も述べた通り、比較回数は最大で「n」回となることから、二分探索では極めて高速に要素の探索が行えることが分かる。100個の要素の探索では、線形探索だと最大で100回の比較が必要になるが、二分探索では最大でも7回の要素の比較で済む(要素数が10,000個ならどうかを考えてみよう)。ただし、要素がソート済みとなっている必要がある。
例えば、「1, 3, 4, 5, 7, 10, 11, 13」というソート済みの整数値を含むデータ列から「10」を探索すると、処理の進み方はおおよそ次のようになる。
それぞれのステップでは探索範囲の両端を示す2つのインデックスmin/max、そこから算出される中央値のインデックスmidを記してある。
原理的には、まず二分探索ではソート済みのデータ列の中央の要素と探索対象の値とを比較する(図の一番上)。図の一番上では要素が偶数個であるため、中央値の候補としてはインデックス3と4の値が考えられるが、ここでは(たまたま)大きい方のインデックス「4」の値を中央値として選択している。
この値が探索対象よりも小さいので、その要素およびその前にある(左側にある、インデックスが小さい)要素については探索対象と同じ値となることはない(これは二分探索の前提となる「全ての要素がソート済みである」ことから分かる)。そこで、これらについては比較が済んだものとして考えてもよい。よって、今度はmin=5からmax=7までの要素が探索範囲となる(図の真ん中。新たな探索範囲は[mid+1, max]と表現できる)。
ここでは中央値としてインデックスが6の要素を選択して、探索対象の値と比較している。この値は探索対象よりも大きいので、その要素およびその後ろにある要素は先ほどと同様に探索の対象外となる。これにより、次の探索範囲は[min, mid-1]となる。この場合、minの値は5でmidの値は6だったので、これは[5, 6-1]、つまりインデックス5の要素1つとなる。この値が探索対象の値と等しければデータ列にその値が存在し、等しくなければ存在しないことになる。もちろん、ここでは等しいのでデータ探索が成功する。ちなみにデータ列に探索対象の値がなければ、おおよそ探索は次のような状況になる。
このようにminとmaxの値をうまく管理することで、二分探索では探索範囲を絞り込みながら高速に要素の探索を行えるようになっている。
二分探索を実装するには、ループを使う方法と再帰呼び出しを使用する方法がある。Pythonでループを使用した実装を以下に示す。ここでは要素が見つかればそのインデックス値を、見つからなかったときにはNone値を返送している。
def bsearch_loop(x, target):
found = False
min = 0
max = len(x)
mid = (min + max) // 2
while min <= max:
#print(f"min: {min}, max: {max}")
#print(x[min:max+1])
#print(f"x[{mid}]: {x[mid]}")
if target == x[mid]:
found = True
break
elif target > x[mid]:
min = mid + 1
else:
max = mid - 1
mid = (min + max) // 2
if found:
return mid
else:
return None
こちらの方法ではシーケンス(リストなど)の3つのインデックスmin、max、midを上で見たようにして操作しながら、配列を2分割し、探索の範囲を狭めている。また、探索対象の値が見つかったら、変数foundの値をTrueにしてループを終了している。要素が見つからない場合には、最終的に探索範囲を示す2つのインデックス値の大小が逆転するので、そうなった場合にもループを終了するようになっている。
再帰関数を使用したコードは次のようになる。
def bsearch_reccursive(x, target, min, max):
#print(f"min: {min}, max: {max}")
#print(x[min:max+1])
mid = (max + min) // 2
if min > max or mid >= len(x):
return None
#print(f"x[{mid}]: {x[mid]}")
if target == x[mid]:
return mid
elif target > x[mid]:
return bsearch_reccursive(x, target, mid + 1, max)
else:
return bsearch_reccursive(x, target, min, mid - 1)
こちらのコードでも同様な処理を行っているが、シーケンスの要素数(関数lenの戻り値)とインデックス値の兼ね合いから関数の再帰を終了する条件について調整を行っている(midの値が要素数以上になった場合にも見つからなかったことを示すNone値を返すようにしている。インデックスの最大値が「要素数-1」であり、不正なインデックスでのアクセスを避けるようにするため)。
動作を確認するには、次のようなコードが使えるだろう。
l = [1, 3, 4, 5, 7, 10, 11, 13]
print(bsearch_loop(l, 10)) # 出力結果: 5
print(bsearch_reccursive(l, 14, 0, len(l))) # 出力結果: None
上のコードにはprint関数呼び出しをコメントアウトして記述しているので、実際にどのように分割/探索が行われるか興味のある方はコメント化を解除して、動作を確認してみてほしい。
また、参考のため、Python版のコードを引き写しただけのものだが、C#で再帰関数を用いて二分検索を行うコード例も示しておこう(ただし、整数配列のみを対象とする)。
class Program
{
static int bsearch(int[] a, int target, int min, int max)
{
int mid = min + (max - min) / 2;
if (min > max || mid >= a.Length)
{
return -1;
}
if (target == a[mid])
return mid;
else if (target > a[mid])
return bsearch(a, target, mid + 1, max);
else
return bsearch(a, target, mid, max - 1);
}
static void Main(string[] args)
{
int[] a = { 1, 3, 4, 5, 7, 10, 11, 13};
System.Console.WriteLine(bsearch(a, 14, 0, a.Length));
System.Console.ReadKey();
}
}
二分探索は、ソート済みのデータ列の中から特定の要素を探索するアルゴリズム。データ列がソート済みであれば、全ての要素を順に検索する線形探索よりも高速に探索を行える。要素数をnとした場合、二分探索で行われる要素の比較回数は最大でもlog 2n回であり、線形探索の最大n回よりも格段に少なくなる。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 線形探索
線形探索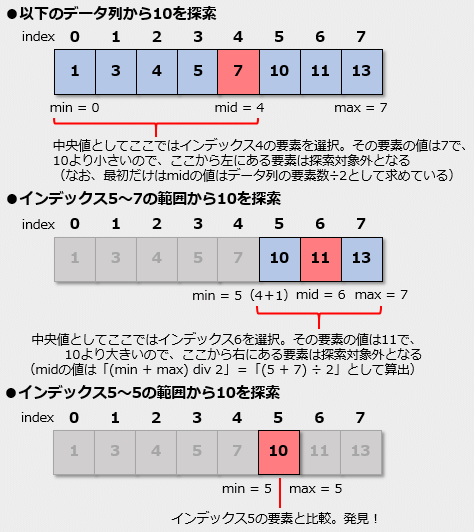 二分探索
二分探索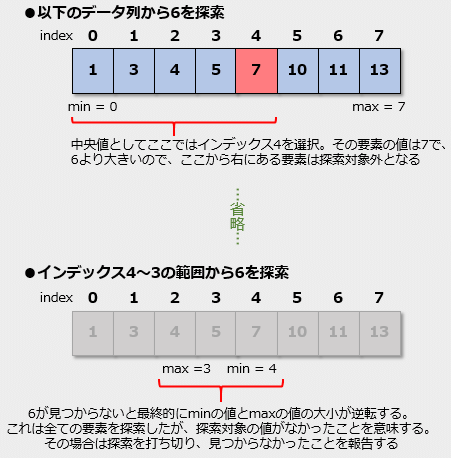 探索対象がなかった場合
探索対象がなかった場合



