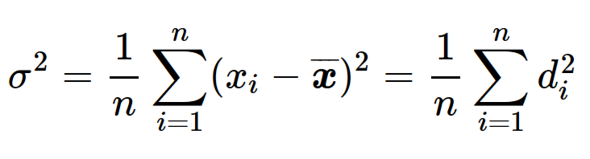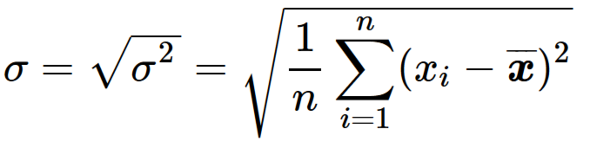Pythonコードと図で分かる平均値と標準偏差の違い――「統計」とはデータから価値ある情報を抜き出すこと:「AI」エンジニアになるための「基礎数学」再入門(3)(2/2 ページ)
統計量
「情報を抜き出す(数値や関数として)」と前述しましたが、この数値として抜き出された情報こそが「統計量」と呼ばれるものです。先ほど例として紹介した、合計や平均値も、その一種です。
一口に統計量といっても、その種類はさまざまで、それぞれの意味合いや算出するにふさわしいケースも異なれば、用法も異なります。
代表値
まずは「代表値」を紹介します。代表値とは「数列内の各要素の値が、だいたいどの程度なのか」を説明する統計量です。
下記のような数列(架空の店舗「a」と「b」の商品の価格などと仮定)を定義しておくとしましょう。
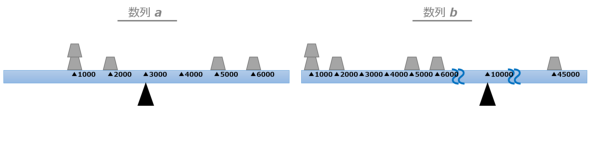
この数列から、淡々と各代表値の定義を説明することもできますが、よりイメージが湧きやすいように以下の図1のような、同じ重さの重りが目盛りの付いたシーソーに載っていることをイメージしてみましょう。
図1は、各要素の値とシーソーの目盛りが対応しており、重りの積み上げられた個数は各要素の出現回数に対応しています。また、現実のシーソーとは異なり、「板に重みはない」としており、「重りの重さだけで釣り合っている」とします。
数列「a」「b」を見比べてみると、5つ目の要素までは同じですが、数列「b」の方は、「45000」と、それまでの要素に比べて大きく値が外れた要素が含まれていることが分かります。こういったものは「外れ値」と呼ばれており、時に厄介な存在です。外れ値は、この後紹介する代表値の性質に大きく関係する存在なので、注意してください。
最頻値:mode
最頻値は読んで字のごとく「最も頻度が高い値」です。図1で見ると、重りの積み上げられた高さが頻度(出現回数)なので、数列「a」「b」の双方とも、最も重りが高くなっている点の「1000」が最頻値であることが分かります。
最頻値は、「外れ値の影響を受けにくい」という長所がある半面、「値が1つに定まらない」「データが少ないと有用な情報にならない」という短所があります。
なお、Pythonで最頻値を算出する際は、下記のように記述できます。
def get_mode(lst):
# 各要素の頻度を計算(list.countは要素を出現回数に変換する関数)
counts = [lst.count(lst_i) for lst_i in lst]
# 頻度の最大値を取得
max_count = max(counts)
# 頻度が最大の要素番号を取得
indexes = [i for i, c in enumerate(counts) if c == max_count]
return [a[i] for i in indexes]
a = [1000, 1000, 2000, 5000, 6000]
mode = get_mode(a)
print(mode)
# 出力: [1000, 1000]
中央値:median
中央値も読んで字のごとく「中央の値」です。つまり、値の大小を基準に並べた際の真ん中の要素のことです。よって、数列「a」の中央値は3番目に大きい(=3番目に小さい)「2000」であると分かります。
しかし、数列「b」はどうでしょうか。要素が6つある中、3番目に小さい「2000」と、3番目に大きい「5000」では、どちらが中央なのか迷ってしまいます。この場合は、それらの数字を足して2で割った値を中央値とします。すなわち、数列「b」の中央値は下記のように「3500」となります。
なお、中央値を数式で表すならば下記のようになります。
中央値は、「外れ値の影響を受けにくい」という長所がある半面、「全てのデータを考慮できた値ではない」という短所があります。
なお、中央値はその定義を数式で見ると複雑そうですが、Pythonで見れば単純です。確認してみましょう。
def get_median(lst):
n = len(lst)
if n%2 == 0:
median = (lst[int(n/2 - 1)] + lst[int(n/2)])/2
else:
median = lst[int(n/2)]
return median
a = [1000, 1000, 2000, 5000, 6000]
b = [1000, 1000, 2000, 5000, 6000, 45000]
print(get_median(a))
# 出力: 2000
print(get_median(b))
# 出力: 3500.0
平均値(算術平均):mean
次に紹介する代表値は、言わずと知れた「平均値」です。皆さんにとって親しみがある「平均」は、正確には「算術平均」と呼びます。他にも「幾何平均」「調和平均」といった平均値も存在しますが、ここでは最も一般的かつ汎用(はんよう)的である「算術平均」を紹介します。「平均の計算方法なんて知っている」という声も聞こえてきそうですが、いま一度、定義とイメージを捉え直して、その性質について考えてみましょう。
まず、算術平均の定義は下記です。
この式が表す意味としては、仮に要素がn個の数列「x」があったら、その算術平均は、全ての要素の合計値を要素の個数nで割った値だということです。定義は問題ないと思うので、そのイメージ付けに移りましょう。
図1において算術平均は一目瞭然です。支点の位置こそが、算術平均を表しています。よって値は、数列「a」については「3000」となり、「b」については「10000」となります。
ここで注意したいのは、外れ値の1つの影響で数列「b」の平均値が、中央値の際と比較して非常に大きくなってしまっていることです。これをシーソーに置き換えて考えてみると、重りを置く位置が支点から遠ければ遠いほど板が傾くので、釣り合いを取りたければ、その分、大きく支点を移動させなければいけません。これが、数列「b」の平均値が非常に大きくなってしまった理由です。
算術平均は、「全てのデータを考慮した値である」という長所がある半面、「外れ値に値が左右されやすい」という短所があります。
よって、例えばある集団の年収などについて一般的な値を知りたければ中央値を算出する(年収や何かをカウントしたようなデータは外れ値が多い傾向があります)。外れ値があまりないようなデータの一般的な値を知りたければ、素直に算術平均を算出するといった、性質に応じての使い分けが重要です。
なおPythonで平均値を算出すると、下記のようになります。
def mean(a):
sum_a = sum(a)
len_a = len(a)
mean_a = sum_a / len_a
return mean_a
a = [1000, 1000, 2000, 5000, 6000]
b = [1000, 1000, 2000, 5000, 6000, 45000]
print(mean(a))
# 出力: 3000.0
print(mean(b))
# 出力: 10000.0
分散:variance、標準偏差:std(Standard Deviation)
最後に紹介したい統計量は、データのバラつき具合を表す分散(=標準偏差2)です。前節で紹介した算術平均とほぼセットで使われる統計量です。
そもそも「データのバラつき具合」とは一体何なのでしょうか? まず「偏差(Deviation)」という概念を知る必要があります。
数列「x」があって、その算術平均がバー「x」の場合の偏差を「d」とすると、定義は下記のようになります。
つまり偏差は、平均値(シーソーの支点)を基準0に置いた際の各データ(重り)の位置を示しています。ここで、数列「a」の偏差「d」を計算してみると下記のようになります。
正と負の値が入り交じった数列が出来上がりました。ここで戸惑わずに再び視覚イメージで捉えてみましょう(図2)。
各要素の値の大きさは赤矢印の長さと対応し、正負は矢印の向きと対応していることがお分かりでしょうか。
つまり、データのバラつき具合とは、平均的な矢印(偏差)の長さ(大きさ)のことを意味しています。矢印が全体的に長くなればなるほど、なんとなく「バラついている」という感覚を持てるのではないでしょうか。
イメージが湧いたら、あとは計算の定義を知るだけです。まずは「分散」(一般的に「σ2」)の定義から確認しましょう。
この式は、「偏差(矢印)を2乗した値の算術平均を分散とします」と表現されています。なぜ、わざわざ偏差を2乗しているのでしょうか?
前述の偏差「da」の要素を合計してみましょう。すると、残念なことに合計値は「0」となり「バラつき具合」とやらは求められそうにもありません。この理由として、「偏差の合計は常に0になる」という性質があるからです。これを避けるためには、偏差に出現する負の値を正の値へと変換してあげればよさそうです。そういった背景があり、あらかじめ全ての要素を2乗して負の値をなくしているのです。
さて、分散が算出されてめでたしめでたしとしたいところですが、分散の単位(矢印の長さ2)を考えてみると、少し違和感があります。先ほど、「データのバラつき具合とは、平均的な矢印(偏差)の長さ(大きさ)のこと」と述べたにもかかわらず、今算出されているのは、その2乗です。よって、ここは素直に分散の平方根を取ってあげましょう。その結果得られる値こそが「標準偏差(σ)」と呼ばれているものです。
標準偏差の定義は下記のようになります。
またPythonでの計算方法も記載するので、参考にしてください。
def var(a):
sum_a = sum(a)
len_a = len(a)
mean_a = sum_a / len_a
dev = []
for a_i in a:
d_sq = (a_i - mean_a)**2
dev.append(d_sq)
var = sum(dev)/len_a
return var
a = [1000, 1000, 2000, 5000, 6000]
print(var(a))
# 出力: 4400000.0
分散、標準偏差の利用の仕方は、また今度
分散、標準偏差の計算方法は分かったが、どのように利用するのかが分からない方が多くいると思いますが、それは、「確率、確率分布」についての記事の中で説明するので、ご期待ください。
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。 Pythonの文法、基礎の基礎
Pythonの文法、基礎の基礎
今回は、Pythonの制御構造と、リスト/タプル/辞書/集合という4つのデータ型について超速で見ていく。 Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。初回は、筆者が実業務で有用としているライブラリ/ツールを7つ紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

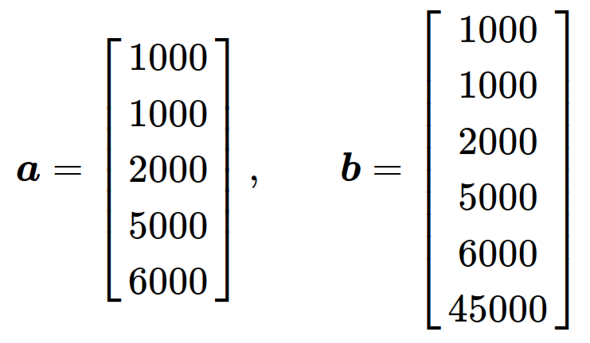
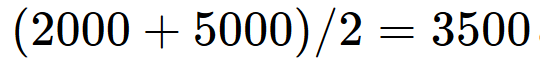
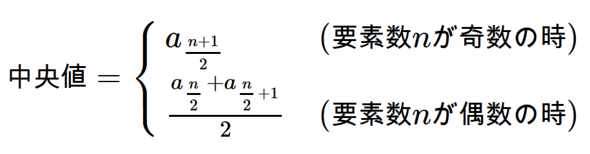 要素数nかつ、要素が値の大小を基に並べられた数列aがある場合
要素数nかつ、要素が値の大小を基に並べられた数列aがある場合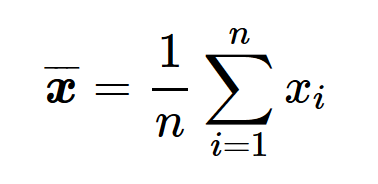
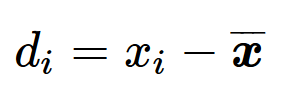
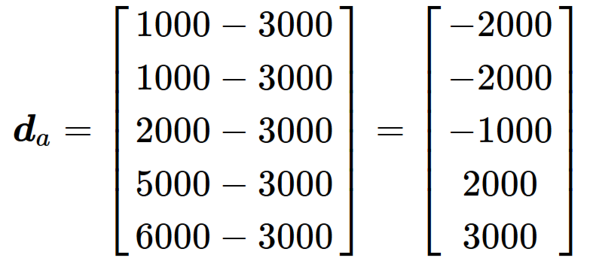
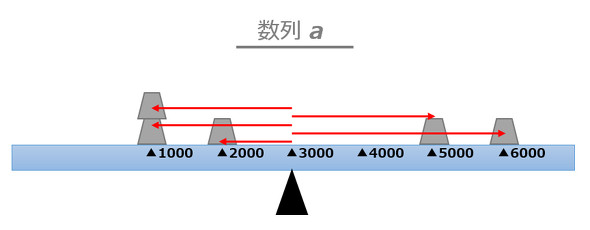 図2 偏差のイメージ
図2 偏差のイメージ