数学における「関数」とは――機械学習はデータ間にある関係性(関数形)を見つける:「AI」エンジニアになるための「基礎数学」再入門(7)(1/2 ページ)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は数学、統計学を学ぶ上で重要な「数学における関数」についてPythonコードと図を交えて解説します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は、集合・数列といった数学・統計学で用いられる数学記号の意味とその使い方について説明しました。
今回は数学・統計学を学ぶ上で重要な項目である「数学における関数」について解説します。
数学における「関数」とは
そもそも数学における「関数」とは、2つ以上の現象間の関係を定量的に対応付けたものです。例として自動販売機で購入する500ミリリットルのペットボトルの飲み物を考えます。自動販売機で500ミリリットルのコーラ飲料を1本購入するとき、あなたは150円を支払います。この時、購入金額とコーラ飲料の間で下記の関係が存在します。
では、このコーラ飲料を3本購入する場合、いくらの金額が必要でしょうか?
1本で150円なので3本の場合、3×150で450円です。皆さん、このような計算を日常的に行っていると思います。コーラ飲料の本数とその購入金額間での関係自体を、数式で表すと、下記のようになります。
購入金額 = 150 × コーラ飲料の本数
この関係性を表す数式こそが関数です。その性質として、ある決まった値(例ではコーラ飲料の購入本数)を与えると、その値に応じた別の値(購入金額)が得られ、同じ値を与えた場合は常に同じ値が返ってきます。
数学・統計学上では、関数内で文字表記をあまり使わないので、より一般化した下記のような表現が用いられます。
y = 150 × x
ここで「y」は購入金額であり、「x」はコーラ飲料の本数を意味します。またxのことを「変数」と呼びます。購入金額とコーラ飲料の本数をyとxで表しましたが、世の中にはこのように関係付けられるものがたくさん存在します。摂取カロリーと体重の関係、太陽の活動とオーロラの発生回数など、ある現象の数値を別の数値を用いて表すことができるのが、関数の便利なところです。
一般に関数の中身(「関数形」と呼びます)を事前に知っていることの方が少なく、yとxが与えられたときにその関数形を知ることが、数学・統計学での課題となる場合がよくあります。機械学習で行っている作業はデータ間にある関係性(関数形)を数値的に見つけ出すことです。人間でもこの作業自体は可能ですが、条件さえそろっていれば、人間よりもずっと速く、正確な関数形を機械は探し出すことができます。
数学・統計学では、関数形自体も、一般化して記号「f」を用いて表されます。fは関数を意味する英語「function」の頭文字です。
fを用いるとyとxの関係は下記のような表現で記述されます。
y = f(x)
先ほど説明した合計購入金額とコーラ飲料の本数の場合、f(x)は下記のようになります。
f(x) = 150 × x
この関数形が定義されていれば、任意のコーラ飲料の本数は下記のように記述できます。
- コーラ飲料の本数が3本の場合:450 = f(3)
- コーラ飲料の本数が10本の場合:1500 = f(10)
複数の関数形が一度に出てくる場合、それぞれの関数形が混同しないように、fとは異なる「g」「h」などを記号として用いて関数形を表します。
基本的な関数
関数にはさまざまな関数形の種類があります。代表的な関数形のグラフをPythonで可視化しつつ、その意味を理解しましょう。
1次関数とそのグラフ
まずは「1次関数」と呼ばれる関数です。1次関数はyに対して次数が1のxと関係している関数形のことです。1次関数は関数の基本的な形であり、統計学ではまず「データ間の関係が1次関数である」という仮定の下で物事を考えることがよくあります。式で書くと下記のようになります。
y = ax + b
ここでaとbは「定数」であり、bはyの変化には関係ありません。a=150、b=0の場合が先ほど解説したコーラ飲料の本数と合計購入費の関係になります。また、「次数」とは「変数が自身の何乗で表現されているのか」を表すもので、上記例ですと「x=x1となり、xの次数は1です。x2の場合、次数は2となり、次数2の変数がその関数形で最大の次数である場合、その関数は「2次関数」と呼ばれます。一般にその関数形で最大の次数が「n」の場合、その関数形は「n次関数」と呼ばれます。
1次関数をPythonで定義して、グラフ化してみましょう。例として、毎年の貯金額を考えます。現在、貯金が50万円あり、毎年30万円が貯金できる状態を考えます。毎年の貯金額がどのようになるか。下記のスクリプトを実行して確認して見てください。
import matplotlib.pyplot as plt # グラフを表示させるPythonライブラリを読み込む
import japanize_matplotlib # 日本語表記対応のPythonライブラリ
plt.style.use('ggplot') # グラフのフォントをggplotに設定
# 1次関数の結果を返す関数 引数はa,b,x
def func_1(a,b,x):
return a*x + b
# 0から9までのxを与え、そのxに対応するyを得る
x = [i for i in range(0,10)]
# xとa=30万円,b=50万円のデータから1次関数を得る
y = [func_1(30,50,i) for i in x]
# 先ほど得たyをグラフにして可視化する
plt.plot(x,y,marker='o') # x,yをplot
plt.xlabel("経過年数") # x軸のラベル表記
plt.ylabel("貯金額[万円]") # y軸のラベル表記
plt.show() # グラフを表示させる
上記のスクリプトを実行すると、図1が得られます。
グラフを見て分かるように、1次関数の特徴はyとxが直線の関係になっていることです。このことから1次関数は「線形関数」とも呼ばれます。a、bを変えることで、1次関数はさまざまな直線を作り出すことができます。
例として向こう9年の3人の貯金額推移を1次関数で表してみましょう。
- Aさん:現在の貯金額=100万円、年間の貯金額=10万円
- Bさん:現在の貯金額=-80万円(借金)、年間の貯金額=50万円
- Cさん:現在の貯金額=50万円、年間の貯金額=25万円
x = [i for i in range(0,10)]
A_y = [func_1(10,100,i) for i in x] # Aさんの貯金額
B_y = [func_1(50,-80,i) for i in x] # Bさんの貯金額
C_y = [func_1(25,50,i) for i in x] # Cさんの貯金額
plt.plot(x,A_y,marker='o',label='Aさん') # Aさんの貯金額をplot
plt.plot(x,B_y,marker='o',label='Bさん') # Bさんの貯金額をplot
plt.plot(x,C_y,marker='o',label='Cさん') # Cさんの貯金額をplot
plt.xlabel("経過年数") # x軸のラベル表記
plt.ylabel("貯金額[万円]") # y軸のラベル表記
plt.legend() # それぞれのグラフの凡例を表示させる
plt.show()
グラフから「向こう9年間で3人の貯金額がどのように変化するのか」がよく分かると思います。このように物事の関係性を関数形で定量的に表し、グラフ化して可視化すると考えている物事の性質がよく理解できます。
2次関数とそのグラフ
2次関数は次数2の変数がその関数形で最大の次数である関数です。数式で書くと下記のようになります。
y = ax2 + bx + c
2次関数が表すものは放物線です。放物線は昔のヨーロッパでは大砲の飛距離を伸ばすために研究されていました。2次関数が放物線を表すことをPythonでグラフを作成し、確認してみましょう。
大砲の弾の運動を2次関数で表す場合、2次関数の係数aは重力によって弾の速度が落ちる強さ(負の値を取ります)、bは弾を打ち出す速度の強さ、cは大砲の位置である高さをそれぞれ表します。今a,bの強さを-1,10として大砲が高さ0メートルの位置から弾を発射した(c=0)場合を下記のスクリプトで確認してください。
# 2次関数の結果を返す関数 引数はa,b,c,x
def func_2(a,b,c,x):
return a*x*x + b*x + c
x = [i for i in range(0,11)]
y = [func_2(-1,10,0,i) for i in x]
plt.plot(x,y,marker='o') # 弾の振る舞いをplot
plt.xlabel("飛距離[m]") # x軸のラベル表記
plt.ylabel("弾の高さ[m]") # y軸のラベル表記
plt.show()
グラフを見ると、発射された大砲の弾が25メートルの高さまで上昇し、発射地点から10メートル先に落下することが分かります。
関数の凄さは一度、関数形が持つ定数(この例ではa,b,c)が決まると、大砲を打つなどしてデータを取らなくても、計算でその振る舞いが分かることにあります。例えば、大砲の弾を打ち出す速度を変えなくても高い場所から発射する(cの値を大きくする)と弾の飛距離を伸ばすことができることは関数を知らなくても分かると思います。ただ、「どの程度高くから大砲を発射すれば、飛距離をどのくらい伸ばすことができるか」といった定量的な判断には関数形を知ることが重要になります。
大砲を設置する砲台の高さが10メートル、20メートルのものを作成したとして、飛距離にどのくらい影響があるか下記のスクリプトで確認してみましょう。
x = [i for i in range(0,13)]
y_1 = [func_2(-1,10,0,i) for i in x]
y_2 = [func_2(-1,10,10,i) for i in x]
y_3 = [func_2(-1,10,20,i) for i in x]
plt.plot(x,y_1,marker='o',label='高さ0メートル')
plt.plot(x,y_2,marker='o',label='高さ10メートル')
plt.plot(x,y_3,marker='o',label='高さ20メートル')
plt.xlabel("飛距離[m]") # x軸のラベル表記
plt.ylabel("弾の高さ[m]") # y軸のラベル表記
plt.legend()
plt.show()
弾の高さが0メートル以上の箇所が、弾が進んだ飛距離です。グラフから20メートルの砲台を使用した場合、飛距離が2メートルほど伸びたことが分かります。この2メートル弱の飛距離を伸ばすことが20メートルの砲台を作成するに値する成果(20メートルの砲台作成にはお金も時間もかかります)なのか、関数を用いることで砲台を作成する前に知ることができます。
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。 AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ!
AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ!
機械学習の数学は難しい!? そう思っている人はここから学んでみよう。本連載では、小学校で習う「四則演算(足し算/引き算/掛け算/割り算)」を使って、機械学習の数学をできるだけ分かりやすく簡単に説明していく。だからサブタイトルは「― 中学/高校数学のキホンから学べる」。今回は距離を求める中学数学をおさらいする。![[Python入門]Pythonってどんな言語なの?](https://image.itmedia.co.jp/ait/articles/1904/02/news024.gif) [Python入門]Pythonってどんな言語なの?
[Python入門]Pythonってどんな言語なの?
機械学習に取り組んでみたいという人に(そうでない人にも)向けて、Pythonプログラミングを基礎からやさしく解説する連載をPython 3.10に合わせて改訂します。
Copyright © ITmedia, Inc. All Rights Reserved.

 (
( (
( (
(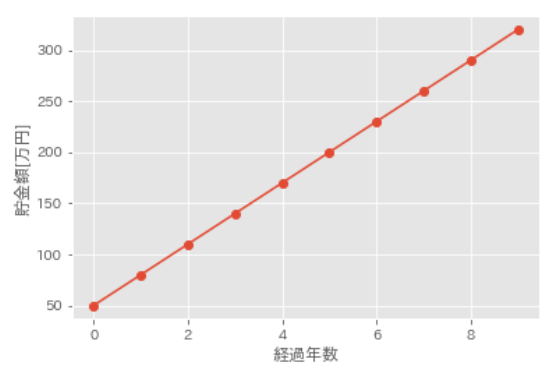 図1 貯金額の推移
図1 貯金額の推移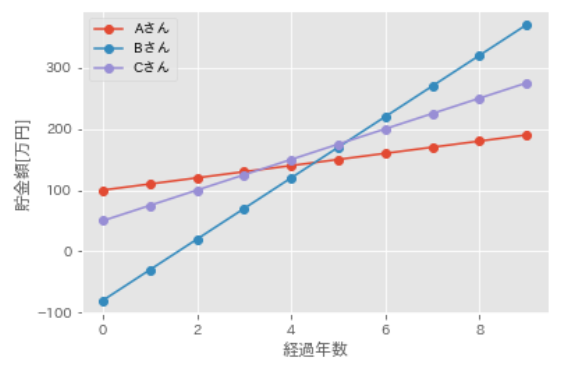 図2 3人の貯金額の推移
図2 3人の貯金額の推移 (
(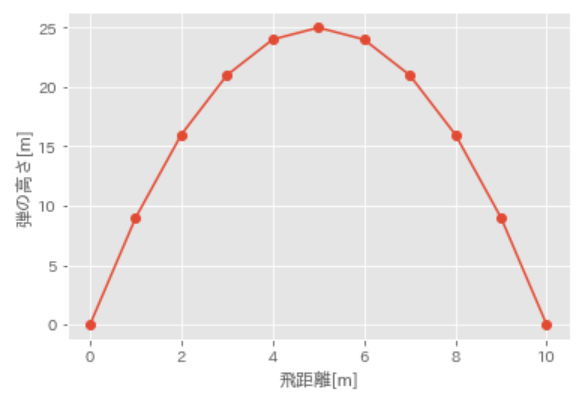 図3 大砲の弾の振る舞い
図3 大砲の弾の振る舞い (
(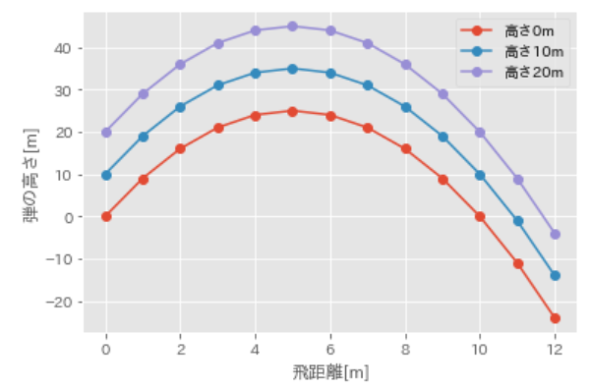 図4 砲台の高さによる飛距離の違い
図4 砲台の高さによる飛距離の違い



