数学における「関数」とは――機械学習はデータ間にある関係性(関数形)を見つける:「AI」エンジニアになるための「基礎数学」再入門(7)(2/2 ページ)
その他のさまざまな関数
これまで関数の基本的なものについて説明してきましたが、関数にはさらに多くの種類が存在します。今回はその中から一部の関数を紹介します。
多項式関数
次数が整数となる変数で記述される関数です。1次関数、2次関数も多項式関数です。
このような多項式関数は次数n(nは任意の数)であるn次関数の形で記述されていることが多いです。なぜなら数学ではある現象を関数化する場合に1次関数、2次関数など具体的な形で議論する前にn次関数という抽象的な関数を考えてから、後でnに具体的な値を入れて具体化するプロセスを用いるからです。この考え方が数学をとっつきにくいものにしている感はあるのですが、慣れるとこちらの方が無駄がないと思うようになります。
n次関数の関数形は下記のようになります。
y = cnxn + cn-1xn-1 + cn-2xn-2 + …… + c3x3 + c2x2 + c1x + c0
前回出てきた数学記号の「シグマ」を用いると、上記のn次関数は下記のように省略して記述できます。
ここでx0=1なのを利用しています。数式が続くと疲れると思いますが、数学の表現に慣れるために覚えておいてください。
指数関数
指数関数とは、a > 0かつa ≠ 1のとき下記の数式で表される関数のことです。
y = ax + b
「a > 1の場合、yは増大する」「0 < a < 1の場合、減少する」という性質を持っています。特にa > 1の場合の増加スピードは急激です。例として、厚さ1センチの紙を何回も半分に折っていくことを考えます。この紙を1回折ったときは2センチ、2回折ったときは4センチと紙の厚さは増加してきます。この紙をx回折ったときの厚さyを数式で表すと下記のような関数(上式でa=2,b=0に相当)になります。
y = 2x
実はx=36、つまり36回この紙を折るとその厚さは68万7194キロにもなり、地球から月までの距離約38万4400キロすら超えてしまいます。このような指数の性質から急激な増加が起きる現象を「指数的な増加」などと呼びます。指数関数の特徴は前回増えた値に対して次の増加量が決まることにあり、元の数が大きいとその増加量も大きくなっていきます。このような急激な増加が起きることは自然界ではあまりないように思うかもしれませんが、多くの現象が指数関数的な振る舞いをします。
具体的な例として、銀行の預金額を考えます。毎年5%の利子(複利)が付く銀行(こんな高利子の銀行は日本にありませんが……)にお金を預けている場合、この利子によって毎年預金が増加します。利子による増加量は増えたお金に対して毎年5%で計算されるため、預金が増えた分だけ毎年の増加量も増加していきます。
最初に1000万円を預けていたらその5%である50万円が増加量となり、翌年の預金額は1050万円になります。その次の年には1050万円の5%が新たな増加量として預金に加わります。これを数式で表すと下記のようになります。
y = 1000(1+0.05)x
ここでxは経過年数で、yはその時の預金額です。毎年50万円の一定量増加する場合と比較して向こう40年で預金額がどの程度違うのか、Pythonでグラフ化してみましょう。ちなみに、毎年50万円の一定量増加する場合はxの1次関数となり、下記のようになります。
y = 1000 + 50x
def func_exp(a,x):
return (1+a)**(x)
x = [i for i in range(0,41)]
y = [1000 + i*50 for i in x]
y_exp = [1000*func_exp(0.05,i) for i in x]
plt.plot(x,y,marker='o',label='毎年50万増加') # 一定額で増加
plt.plot(x,y_exp,marker='o',label='毎年5%増加') # 指数的に増加
plt.xlabel("経過年数") # x軸のラベル表記
plt.ylabel("預金額[万円]") # y軸のラベル表記
plt.legend()
plt.show()
グラフを見ると、毎年50万円の一定量で増え続ける場合と比較して預金額は2倍以上増加しています。また、この変化は元の預金額が大きくなっている場合に顕著になっています。このように、現在の値に対して次の増加量(減少量)が決まることが多いので、指数的な振る舞いが自然界ではよく見られます。
多変数関数
これまでyに関係している変数がただ1つのxのみの場合を考えてきましたが、現場で使われるデータではyに関係している変数は1つではない場合のことが多いです。そのような変数を2つ以上持つような関数のことを「多変数関数」と呼びます。変数の数が2つの場合(「2変数関数」と呼びます)を数式で表すと下記のようになります。
y = a1x1 + a2x2 + b
fを用いて省略形で表す場合は下記のようになります。
y = f(x1,x2)
これはx1,x2の2変数がyに関係していることを表しており、ある2つの値x1,x2の組に対して、ただ1つの値yが対応することを意味しています。ここで下付きの数字は次数ではなく、各変数を区別するために付いている便宜上のものです。a1,a2も同様に別々の値を持つ定数となります。
この関数形は2変数を含みますが、最大の次数は1なので、この関数は1次関数に分類されます。多変数関数は可視化するのが困難な関数です。2変数の場合は3次元(2つの変数x1,x2と、その変数で表されるy)なのでグラフ化できますが、3変数以上、つまり4次元以上になると基本的にグラフによる可視化は行えません。統計学では、この多変数関数の性質を知るさまざまな手法があり、それらの手法を用いて3変数以上のデータの分析を行います。
今回はグラフによる可視化が可能な2変数関数の場合をPythonでグラフ化してみましょう。グラフ化する関数として下記の関数を考えます。
Pythonで2変数関数の可視化には3軸目を追加して立体的にグラフを描画する3次元plotと、3次元目の値を色で表現する等高線図があります。今回は等高線図で2変数関数を表現してみます。下記のスクリプトを実行してください。
import numpy as np
def func_3d(a1,a2,x1,x2):
return a1*x1**2 + a2*x2**2
x1 = np.linspace(-10, 10) #x1を-10から10まで生成
x2 = np.linspace(-10, 10) #x2を-10から10まで生成
X1,X2 = np.meshgrid(x1, x2) # x1,x2の組み合わせを生成
y = func_3d(1,1,X1,X2) # a1=1,a2=1,b=0で関数を作成
plt.pcolormesh(X1,X2,y,cmap='hsv') # 等高線図の生成。cmapで色付けの規則を指定
pp=plt.colorbar (orientation="vertical") # カラーバーの表示
pp.set_label("y", fontname="Arial") #カラーバーのラベル
plt.xlabel('X1') # x軸のラベル表記
plt.ylabel('X2') # y軸のラベル表記
plt.show()
グラフを見ると、中心(0,0)から円状に色が変化していくことが確認できます。色の定義から、この色の変化は中心から離れるにつれてyの値が大きくなっていることが分かります。スクリプト内ではa1とa2は同じ値に設定しましたが、この関数はa1,a2の比率(a1/a2)を変えることによって円の形状が変化します。
さまざまな値を入れてその変化を試してみてください。
次回は、確率・確率分布について
今回のまとめは、下記2点です。
- 関数とは2つ以上の現象間の関係を定量的に対応付けたものであり、機械学習で行っているのはデータ間の関係性(関数形)を見つけ出すこと
- あるデータの関数形を知ると未知のデータに関しても「どのような振る舞いをするか」をすぐに推測することができる
次回は、確率・確率分布について解説します。
筆者紹介
原 拓自(はら たくじ)
1988年、岐阜県生まれ。大学院では宇宙物理を専攻し、卒業後はデータサイエンティストとしてキャリアをスタートする。
さまざまな会社で分析コンサルを経験した後、世界最大の外資系ECサイト会社でデータサイエンスの知識を深める。
現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。
西村圭介
1991年、富山県生まれ。大学院を卒業し、企画コンサルタントとしてキャリアをスタートする。その後、統計学とプログラミングスキルの知見を基にデータサイエンティストとしてのキャリアを進める。現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。 AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ!
AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ!
機械学習の数学は難しい!? そう思っている人はここから学んでみよう。本連載では、小学校で習う「四則演算(足し算/引き算/掛け算/割り算)」を使って、機械学習の数学をできるだけ分かりやすく簡単に説明していく。だからサブタイトルは「― 中学/高校数学のキホンから学べる」。今回は距離を求める中学数学をおさらいする。![[Python入門]Pythonってどんな言語なの?](https://image.itmedia.co.jp/ait/articles/1904/02/news024.gif) [Python入門]Pythonってどんな言語なの?
[Python入門]Pythonってどんな言語なの?
機械学習に取り組んでみたいという人に(そうでない人にも)向けて、Pythonプログラミングを基礎からやさしく解説する連載をPython 3.10に合わせて改訂します。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

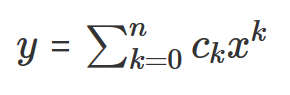
 (
(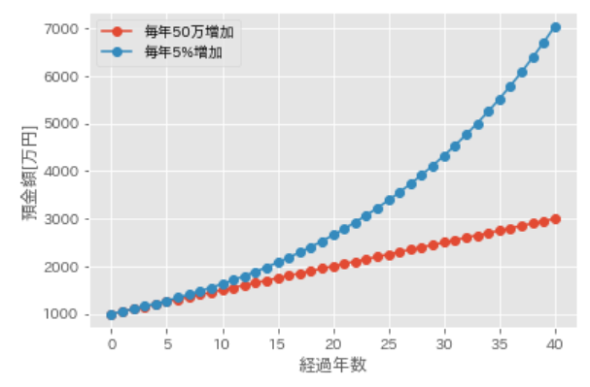 図5 指数的による預金の増加量
図5 指数的による預金の増加量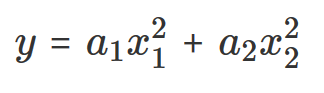
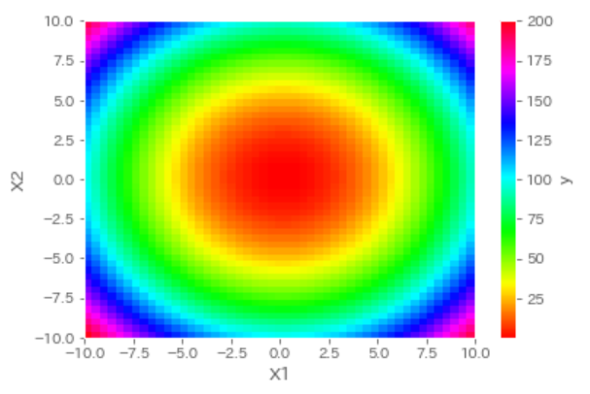 図6 2変数関数のグラフ化
図6 2変数関数のグラフ化



