Hello Deep Learning:ニューラルネットワークの作成手順:作って試そう! ディープラーニング工作室(2/2 ページ)
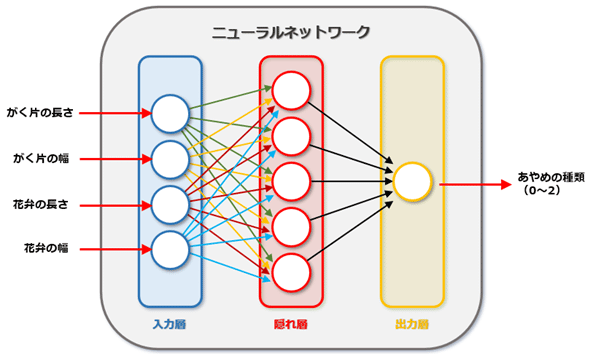
ニューラルネットワークの定義
ここではPyTorchが提供するフレームワークの機能を利用して、ニューラルネットワークを表すクラスを定義していきます。その前に、ここで作成するニューラルネットワークについて思い出しておきましょう。
ここでは全部で3つの層で構成されるニューラルネットワークを作成するのでした。
- 入力層:ノードは4つ(がく片/花弁の長さ/幅を受け取ります)、出力は5つ
- 隠れ層:ノードは5つ(入力層からの出力を各ノードが受け取ります)、出力は1つ
- 出力層:ノードは1つ(隠れ層からの出力を受け取り、それをそのまま出力します)
ある層のノードが次の層の全てのノードと接続されるようなニューラルネットワークをここでは作成します。このようなニューラルネットワークはPyTorchではLinearクラス(torch.nn.Linearクラス)を使うことで簡潔に記述できます。
実際のコードを以下に示します。コードを入力したら、実行しておきましょう。
from torch import nn
INPUT_FEATURES = 4
HIDDEN = 5
OUTPUT_FEATURES = 1
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(INPUT_FEATURES, HIDDEN)
self.fc2 = nn.Linear(HIDDEN, OUTPUT_FEATURES)
def forward(self, x):
x = self.fc1(x)
x = torch.sigmoid(x)
x = self.fc2(x)
return x
まず、PyTorchが提供するtorch.nnモジュールをインポートしています(「nn」は「neural network」の頭字語でしょう)。PyTorchではtorch.nnモジュールでニューラルネットワークの基底クラスとなるModuleクラスを定義しています(下のクラス定義を見ると、torch.nn.Moduleクラスを基底クラスとしていることが分かりますね)。
その下の3行では、先ほど述べた入力層のノード数(INPUT_FEATURES)、隠れ層のノード数(HIDDEN)、出力の数(OUTPUT_FEATURES)を変数に代入しています。最後のNetクラスの定義が、ここで使用するニューラルネットワークを記述したものです。
class Net(nn.Module):
def __init__(self):
# ……省略……
def forward(self, x):
# ……省略……
Netクラスはnn.Moduleクラス(torch.nn.Moduleクラス)を基底クラスとすることで、PyTorchが提供するニューラルネットワーク(PyTorchでは「ニューラルネットワークモジュール」と呼んでいます)の全ての機能を継承するようになっています(つまり、これだけでニューラルネットワークの基本機能を備えるということです)。そして、__init__とforwardの2つのメソッドを定義しています。
__init__メソッドでは、最初に基底クラスの__init__メソッドを呼び出して、その初期化を行っています(詳細な説明は省きますが、Python 2だと「super(Net, self).__init__()」と書く必要がありますが、ここではPython 3を対象としているので、このようなシンプルな書き方をしています)。その後に、2つのインスタンス変数self.fc1とself.fc2に、先ほど述べたLinearクラスのインスタンスを代入しています。
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(INPUT_FEATURES, HIDDEN) # 入力層(入力:4、出力:5)
self.fc2 = nn.Linear(HIDDEN, OUTPUT_FEATURES) # 隠れ層(入力:5、出力:1)
def forward(self, x):
# ……省略……
Linearクラスのインスタンスを生成する際には、そのインスタンスが表す層(ここでは入力層と隠れ層に相当するインスタンスを生成しています。出力層については後述)への入力の数と、その層から次の層への出力の数を指定します。インスタンス変数self.fc1へ代入するLinearクラスのインスタンスの生成では「self.fc1 = nn.Linear(INPUT_FEATURES, HIDDEN)」のようにして、入力はINPUT_FEATURES(4)、出力はHIDDEN(5)を渡しているので、これが入力層を表すインスタンスということです。インスタンス変数self.fc2についても同様です。
ここで「self.fc3というインスタンス変数に出力層を表すLinearクラスのオブジェクトを代入する必要はないの?」と思う方もいらっしゃるかもしれません。が、ここでは隠れ層からの出力をそのまま外部への出力としてしまうことにしているので、出力層に対応するインスタンスは作成していません。
注意してほしいのは、__init__メソッドで行っているのは「ニューラルネットワークを構成する層の定義」だけであることです。
__init__メソッドで定義した層が実際にどのようにつながっているか(ニューラルネットワークがどのように計算を連ねていくか)はforwardメソッドで定めています。forwardメソッドは入力x(あやめの特徴を示す4つのデータ)を受け取り、それをself.fc1で処理して、その結果をにtorch.sigmoid関数に通した結果を今度はself.fc2メソッドで処理し、その結果を戻り値(ニューラルネットワークの計算結果)としています(ここで「self.fc1とself.fc2はLinearクラスのインスタンスなのに、メソッドのように呼び出している」ことに気付くかもしれません。が、PyTorchではこのような書き方ができるようになっています。詳しくは後続の回で説明します)。
class Net(nn.Module):
def __init__(self):
# ……省略……
def forward(self, x):
x = self.fc1(x) # 入力データ→入力層
x = torch.sigmoid(x) # 入力層→活性化関数
x = self.fc2(x) # 活性化関数→隠れ層→出力
return x
ここで出てきた「torch.sigmoid関数」が、前回にも出てきた「活性化関数」と呼ばれるものです。ここでは、ソフトウェアにおけるニューラルネットワークの世界では、活性化関数は「ある層で処理した結果を、別の層へ渡すときにさらに変換を加える」ものだと思っておいてください。
いろいろと分からないことを積み残したままかもしれませんが、今回はあくまでもニューラルネットワークを作って学習とテストをするまでをザッと見ることが目的なので、そこはあまり気にしないようにしましょう。ともかく、__init__メソッドとforwardメソッドで上のようなコードを書いたことで、「入力データ→入力層→活性化関数→隠れ層→(出力層→)出力」という流れが書けたことになります。
ここで実際の学習に向かう前に、ちょっとこのクラスを使ってみましょう。
net = Net() # ニューラルネットワークのインスタンスを生成
outputs = net(X_train[0:3]) # 訓練データの先頭から3個の要素を入力
print(outputs)
for idx in range(3):
print('output:', outputs[idx], ', label:', y_train[idx])
このコードでは最初にNetクラスのインスタンスを生成し、次に先ほど分割したデータのうち、X_trainの先頭から3つをニューラルネットワークに入力しています。その結果を変数outputsに受け取ったら、それをまずは表示して、次にそれらの値と、対応する正解ラベル(変数y_train)とを比較表示しています。
実際に実行した結果を以下に示します(読者がこのコードを試した場合、以下とは具体的な数値は異なるものが得られるでしょう)。
最初の出力からは、このニューラルネットワークは、「計算結果を唯一の要素とする配列」を要素とする配列(テンソル)になっていることが分かります(3つのデータを入力したので、出力結果である配列の要素数も3です)。そして、その次の出力を見ると、学習をする前のニューラルネットワークが計算した値が正解ラベルの値とはかけ離れたものになっていることも分かります。今から行う「学習」とは、この計算結果を右側の正解ラベルの値へと近づけていく過程に他なりません。
学習(訓練)と精度の検証
前回も述べたように、今から行う「学習」では、上で見たような形でニューラルネットワークにデータを入力し、それらから得られる計算結果(推測結果)と正解ラベルとを比較しながら、ニューラルネットワークが内部で持っている重みやバイアスを更新していきます。
このときには「損失関数」と呼ばれる関数を用いて、計算結果と正解ラベルとの誤差を比べたり、それらを基に「最適化」と呼ばれる処理を行いながら、重みやバイアスを調整したりしていきます。これらの要素については後続の回で詳しく説明するものとします。ここではPyTorchを使って学習を行う典型的な(ただし、一般的なものよりもシンプルな)コードを紹介します。
学習の手順はだいたい次のようなものです。
- ニューラルネットワークにX_trainに格納したデータを入力する(112個)
- 損失関数を用いて、計算結果と正解ラベルとの誤差を計算する(計算結果は損失 と呼ばれる)
- 誤差逆伝播(バックプロパゲーション)や最適化と呼ばれる処理によって重みやバイアスを更新する
- 上記の処理を事前に定めた回数だけ繰り返す
この手順を実際のコードとして表現したものが以下です。
net = Net() # ニューラルネットワークのインスタンスを生成
criterion = nn.MSELoss() # 損失関数
optimizer = torch.optim.SGD(net.parameters(), lr=0.003) # 最適化アルゴリズム
EPOCHS = 2000 # 上と同じことを2000回繰り返す
for epoch in range(EPOCHS):
optimizer.zero_grad() # 重みとバイアスの更新で内部的に使用するデータをリセット
outputs = net(X_train) # 手順1:ニューラルネットワークにデータを入力
loss = criterion(outputs, y_train) # 手順2:正解ラベルとの比較
loss.backward() # 手順3-1:誤差逆伝播
optimizer.step() # 手順3-2:重みとバイアスの更新
if epoch % 100 == 99: # 100回繰り返すたびに損失を表示
print(f'epoch: {epoch+1:4}, loss: {loss.data}')
print('training finished')
コードには上記手順に対応する箇所にその旨のコメントを記しています。手順1の前に「重みとバイアスの更新で内部的に使用するデータをリセット」していますが、これはそういう作法だと考えておいてください。また、繰り返しを100回行うたびに、その時点で計算結果と正解ラベルとの誤差がどのくらいになったか(損失:loss.data)を表示するようにもしてあります。簡単には、「誤差」がゼロに近いほど、計算結果と正解ラベルの差が少ないと考えられます。つまり、ここでの学習とは誤差がゼロに近いものになるように、重みやバイアスを更新していくということでもあります。
実際に試してみた結果を以下に示します。
損失が徐々に減少していることが分かるでしょうか。最終的には損失が0.07程度になりました。100回の学習を行った時点の損失が0.6を越えていたことを考えるとずいぶんと推測結果と正解ラベルの値が近づいたことが分かります(この数値が意味するところについては、次回以降に説明をします)。
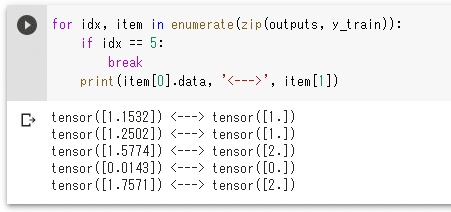
実際に、(最後に学習を行ったときの)計算結果を最初から5つ、対応する正解ラベルと共に表示してみましょう。
for idx, item in enumerate(zip(outputs, y_train)):
if idx == 5:
break
print(item[0].data, '<--->', item[1])
このコードを実行した結果は次の通りです(読者が上のコードを実際に試したときには、これとは異なる結果になるでしょう)。
どうでしょう。学習前にニューラルネットワークが算出した結果と比べると、かなり近しい値が得られているようです。ただし、ここで欲しいのは0、1、2のいずれかの整数値です。上の結果を見るに、小数点以下1桁目で四捨五入をするといい感じに整数値が得られそうです。というわけで、ここでは計算結果を含んだ配列の各要素に0.5を加算したものを整数型に変換するコードを書いてみましょう。
predict = (outputs + 0.5).int()
for idx, item in enumerate(zip(predict, y_train)):
if idx == 5:
break
print('output:', item[0], ', label:', item[1])
「outputs + 0.5」という部分を見て「へ?」と思った方もいるかもしれません。これは、「ouputsの全要素に0.5を加算する」という処理を行います。NumPyが提供する多次元配列では「配列の各要素に加算/減算する」ような処理をこのように分かりやすく記述できるようになっています(この機能をNumPyでは「ブロードキャスト」と呼んでいます)。PyTorchのテンソルはNumPyの配列とは異なるものですが、こうした使い方はPyTorchでも可能です。後は、変換後のデータ(predict)と正解ラベルの先頭から5つの要素を表示するコードになっています。
実行結果を以下に示します。
数値部分にのみ着目すると、どうもいい感じです。最後に、112個の入力データから計算した結果がどれだけ正解ラベルと一致しているかを確認してみましょう。
compare = predict == y_train
print(compare[0:5])
print(compare.sum())
ここでもコードを見てギョッとする人がいるかもしれません。「predict == y_train」というのは、「predict(変換後の整数値を格納した配列)とy_train(正解ラベル)の各要素を比較して、それらが等しければ対応するインデックス位置の値をTrueに、等しくなければFalseとする配列を返す」という処理をします。つまり、[True, True, True, False, True, ……]のような配列がcompareに代入されます。上のコードではその先頭から5つの要素を表示するようにしています。後から示す実行結果で今述べたような配列が得られていることを確認してください。
「compare.sum()」というのは、その配列の要素の総和を求める処理です。ただし、PythonではTrueは1と、Falseは0と見なされることを思い出してください。よって、「総和を求める」=「Trueの要素の数を数える」ということです。
では、実行結果を示します。
どうでしょう。「108」個が正しいことが分かりましたね。112個のうちの108個が正しいので、正解率 は96.4%といえます。なかなかの精度といってもよいでしょう。取りあえず、ここではこれでニューラルネットワークは完成したものとしましょう。
次に、完成したニューラルネットワークの精度を確認します。上で確認したのは、あくまでも「訓練に使用したデータに対する正解率」です。既に述べた通り、訓練に使用していない未知のデータに対しても、このニューラルネットワークが適切な値を返せなければ、このニューラルネットワークには意味がありません。そのため、本稿の冒頭ではデータを訓練データとテストデータに分割したのでした。
そこで、上と同様な手順で、ニューラルネットワークにテストデータを入力して、その値をテストデータの正解ラベルと比較してみましょう。
実際のコードは以下のようになります。
outputs = net(X_test)
predict = (outputs + 0.5).int()
compare = predict == y_test
print(f'correct: {compare.sum()} / {len(predict)}')
for value, label in zip(predict, y_test):
print('predicted:', iris.target_names[value.item()], '<--->',
'label:', iris.target_names[int(label.item())])
ここでは学習を行うわけではないので、for文によるループで誤差を計算して、重みやバイアスを更新するといった処理は必要ありません。そのため、Netクラスのインスタンスにテストデータを入力し、得られた計算結果を小数点1桁目で四捨五入して整数値化したら、それをテストデータ用の正解ラベルと比較するだけです。最後には全てのデータを出力するコードも書いてあります(最後の行で使っているitemメソッドは、配列の値を取り出すものです)。
実行結果を以下に示します(品種の推測結果と正解ラベルを比較した出力は途中で省略しています)。もちろん、読者が上のコードを実際に試したときには、これとは異なる結果になるでしょう。
38個(150個の3/4)のテストデータのうち、38個が正しいということで、100%の正解率となりました(ちょっとビックリしました。が、学習に使用したデータでは完璧な推測ができたわけではないことも思い出してください。つまり、このニューラルネットワークはどんなデータに対しても常に正しく判断できるとは限らないことには注意しましょう)。どうやらこのニューラルネットワークは、訓練データ以外のデータが入力されても、それがどんな品種のあやめなのかをある程度は正しく判断できることが確認できました。
今回は駆け足で、ニューラルネットワークを作成する手順を眺めてきました。ニューラルネットワークを作成し、それを学習させ、その精度を評価するまでには、データセットの準備、ニューラルネットワークの定義、学習、評価というステップを踏みます。今回はその大枠を眺めました。次回は今回の書いたコードを基に、各段階について少し詳しく見ていくことにしましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.

 実行結果
実行結果
 実行結果
実行結果 実行結果
実行結果 実行結果
実行結果 実行結果
実行結果



