ニューラルネットワークの学習でしていること:作って試そう! ディープラーニング工作室(2/2 ページ)
重みの更新の過程
「重みを更新」するといっても、どうすればよいでしょう。ここではゴールは見えています。1.95という重みを2.0に近づけていくことです。
ここで、先ほどの損失関数について少し考えてみましょう。MSELossクラスを使って作成した損失関数は、出力値を含むベクトルと正解ラベルを含むベクトルを受け取り、対応する2つの値を減算して二乗した値の平均を損失としていました。ただし、ここでは1つの計算値と対応する正解ラベルの誤差を求めているだけであることには注意してください。よって、出力値をoutput、正解ラベルをlabelとしたときに損失関数で行っている処理は「(output - label) ** 2」と同じと考えられます(「平均」の概念が抜け落ちていますが、これは話をシンプルにするためです)。
この値が最小(理想的には0)となるような重みを見つけることがここで行っている学習の目的です。一方の比較対象(正解ラベル)はシンプルに2です。そこで、「(output - label) ** 2」(label=2)という式(関数)を最小化するoutputの値(さらには重みwの値)が何かを考えます(もちろん、output=2.0ですし、w=2.0です)。
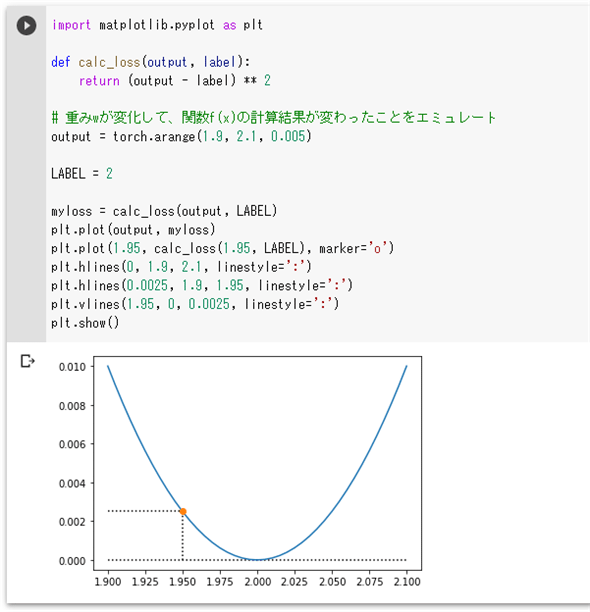
以下のコードでは、今述べた形で損失を返す関数「calc_loss」を定義して、変数outputには「重みが1.9〜2.1の範囲で変化したときの、f(x)=w × x(x=1)の計算結果(をエミュレートしたもの)」を、定数LABELには正解ラベルの値である2を代入しています。そして、calc_loss関数が計算した損失(myloss)をグラフにプロットしています。
import matplotlib.pyplot as plt
def calc_loss(output, label):
return (output - label) ** 2
# 1.9〜2.1の範囲の重みwに対し、関数f(x)にx=1を与えたときの計算結果
output = torch.arange(1.9, 2.1, 0.005)
LABEL = 2
myloss = calc_loss(output, LABEL)
plt.plot(output, myloss)
plt.plot(1.95, calc_loss(1.95, LABEL), marker='o')
plt.hlines(0, 1.9, 2.1, linestyle=':')
plt.hlines(0.0025, 1.9, 1.95, linestyle=':')
plt.vlines(1.95, 0, 0.0025, linestyle=':')
plt.show()
現在のところ、重みは1.95、xの値は1であることから、関数f(x)の計算値である1.95とそのときに得られる誤差も図にプロットするようにしました(横軸の値は関数f(x)に対してx=1としたときの計算結果に対応します)。これを実行した結果が以下です(グラフ描画のコードについての説明は省略します)。
これを見れば分かる通り、損失が最小になるのは、関数f(x)にx=1を与えたときの計算結果が2.0となったときで、現在の重みの値「1.95」をこれに近づけるように更新していけばよいということになります。
人がグラフを見れば、「現在の横軸(output=f(x)の値)が2.0に近づくように、wを増加させていけばよいだろう」ということは一目瞭然です。しかし、コンピューターにはなかなかそうはいきません。そこで重要なのが、重みを増加させるのか、減少させるのかの判断です。例えば、重みwが2.05まで増加したらどうなるでしょうか。
もちろん、今度は関数f(x)の計算結果は2.05となり(x=1)、損失を最小とする値を超えてしまいました。となると、重みを減らす方向に戻る必要があります。
ここで重みを増加させるのか、減少させるのかの判断に役立つ指標があります。それは「勾配」と呼ばれるものです。あるいは、「グラフの(接線の)傾き」といってもよいでしょう。今の例では、横軸の値となるoutput=関数f(x)の値が2.0になるまではグラフは右肩下がりでその勾配はマイナスです。一方、2.0を越えればグラフは右肩上がりでその勾配はプラスになります。損失を最小にする箇所(関数f(x)の計算結果が2.0)では勾配はゼロとなります。
つまり、勾配がマイナスなら重みを増加させて、プラスなら減少させていけばよいということです。そして、勾配がゼロとなる地点が見つかれば、そこで最適な重みが見つかったことになります(実際には、これほど簡単な話ではありません。グラフの頂点が複数あるような場合には、実は最適な値ではないところで勾配がゼロとなってしまう可能性もあります。こうした問題を解決する方法も考えられています。が、ここでは損失を求めるグラフが単純な2次曲線であるため、傾きがゼロとなる重みを求めるだけでよしとします)。
なお、勾配を表す英単語は「gradient」であることから、それを省略した「grad」などが勾配に関連する属性や変数、関数などの名前ではよく使われることも覚えておきましょう(以下のコードでは、勾配を求める関数に「calc_grad」と名前を付けてあります)。
その勾配(傾き)を求めるには幾つかの方法があります。一つは損失関数の微分です。数学の難しい話を抜きにして、ざっくりとした話をするので、難しいという方は流して読んでもらってもかまいません。
上のグラフを描画するコードでは損失は「(output - label) ** 2」として求めていました。この式において、output=f(x)であることを思い出してください。さらに、f(x)は重みwと入力値xの乗算でもありました。
つまり、この関数では「(w * x -label) ** 2」と同じ計算をしているということです。これを展開したものを、やはりPythonのコードで表現すると「w ** 2 * x ** 2 - 2 * w * x * label + label ** 2」となります。ここではwが変化することで、損失関数の勾配がどう変化するかに着目しているので、上記の式を「w」で微分(偏微分)します。その結果は「2 * x ** 2 * w - 2 * x * label」です。そして、ここではw=1.95、x=1、label=2でしたから、これらの値をこの式に代入することで、勾配が得られます(式からはoutputが消えて、w、x、labelに関するものになっていることに注意してください)。
なお、数学的な深い話は「AI・機械学習の数学入門 ― 中学・高校数学のキホンから学べる」をご覧ください(ただし、2020年4月23日時点では微分の話はまだ取り上げていません)。
これを実際に行うコードを以下に示します。
def calc_grad(w, x, label):
return 2 * x ** 2 * w - 2 * x * label
grad = calc_grad(w, x, LABEL)
print('grad:', grad)
実行結果を以下に示します。
これにより、重みを1.95、x=1、label=2としたときの損失関数の傾きは「-0.1000」になったことが分かりました。
関数の最小値(あるいは最大値)を求めることを「最適化問題」と呼ぶことがよくあります。そして、今見たような勾配を手がかりとして、その値を探すことを一般に「勾配法」と呼びます。機械学習やニューラルネットワークの世界では、この手法を用いて、損失関数の最小値を求める値を探すことがよくありますが、これを「降下勾配法」と呼びます。降下勾配法のアルゴリズムにも幾つかの種類があり、冒頭で紹介したコードに含まれていた「torch.optim.SGDクラス」はそうした最適化アルゴリズムの1つを表すクラスです(この後も使用しますが、この例ではオーバースペックなものでもあります)。
ここでは、損失関数の微分によって、重みを更新するための手がかりである勾配を求めましたが、現在ではより効率的に勾配を求める方法として、「誤差逆伝播法」(backpropagation、バックプロパゲーション)が使われています。この詳細については後続の回に譲りますが、これを実際に行っているのが、以下のコード(本稿冒頭で示したコード)で、強調書体とした行です。
outputs = net(X_train) # 手順1:ニューラルネットワークにデータを入力
loss = criterion(outputs, y_train) # 手順2:正解ラベルとの比較
loss.backward() # 手順3:誤差逆伝播
optimizer.step() # 手順4:重みとバイアスの更新
実はPyTorchでは、テンソルに対して、どのような操作が行われたかを記録できるようになっています。このことを利用して、あるノードから別のノードへ渡される値を計算するときに、「ここでは何と何を乗算した」「ここではアレとコレを加算した」など、何が行われたかの情報がそのテンソルに記録されます。そして、勾配を計算する際には、計算した結果からその情報を遡りながら、各ノードにおける勾配を効率よく計算できるようになっているのです。この情報を保存するためには、テンソルを作成する際に、「requires_grad」キーワード引数にTrueを指定する必要があります。
そのため、先ほどの重みを格納する1行1列の行列の定義では、次のようにして、テンソルを生成していたのです。
w = torch.tensor([[1.95]], requires_grad=True)
というわけで、ここでbackwardメソッドを呼び出して、実際に誤差逆伝播を実行してみましょう。ここでは、criterion呼び出しによって返された値(変数loss)に対して、これを行ってみます。なお、勾配はテンソルのgrad属性に保存されるので、backwardメソッドの呼び出しの前後で、これが本当に変化するかも確認します。
print('before w.grad:', w.grad)
loss.backward()
print('after w.grad:', w.grad)
実行結果を以下に示します。
どうでしょう。呼び出し前のw.grad属性の値は「None」でしたが、呼び出し後は「-0.1000」になっています。先ほど手作業で実行した勾配も「-0.1000」だったので、どちらの方法でも同じ勾配が得られたと考えてよいでしょう。ここまでの話が冒頭に示したコードにおける手順3に相当します。
最後に、得られた勾配を利用して、重みを更新します(手順4に相当)。ここで登場するのが先ほども少し出てきた最適化アルゴリズムです。ここではこれまでと同様に、torch.optim.SGDクラスのインスタンスを生成することにします。
optimizer = torch.optim.SGD([w], lr=0.3)
SGDクラスのインスタンスを生成する際には、更新を行う対象と学習率(learning rate)と呼ばれる値を指定する必要があります。ここでは更新の対象には1行1列の行列であるwを含んだリストを、学習率を表すキーワード引数lrには0.3を指定しています(学習率については後述します)。
ちなみに、これまでに見てきたあやめの品種の分類では次のようにしてインスタンスを生成していました。
optimizer = torch.optim.SGD(net.parameters(), lr=0.003) # 最適化アルゴリズム
あやめの品種を分類するために定義したNetクラスでは(コードは省略)、そのインスタンス変数fc1とfc2に入力層から隠し層、出力層へと渡る値を計算するために必要な重みやバイアスが保存されているのは前回も見た通りです。そこで、Netクラスのインスタンスに対してparametersメソッドを呼び出して、それらを反復するジェネレータを手に入れて、それをインスタンスの生成に使用していると考えてください。
では、実際に重みを更新しましょう。これにはstepメソッドを呼び出すだけです(手作業で同じことを行うのは省略します)。ただし、今度は重みwが本当に更新されるかを確認するために、変数wの値をstepメソッド呼び出しの前後で調べます。
print(w)
optimizer.step()
print(w)
実行結果を以下に示します。
重みが1.9500から1.9800に増加したことが確認できました。ところで、増加した「0.0300」はどこから出てきた値なのでしょうか。実はこれは「勾配」と「学習率」を乗じたものになっています。先ほど計算した勾配(w.grad)は「-0.1000」で、学習率には「lr=0.3」を指定していました。これらを乗じた結果である「-0.0300」を重みから減算することで、実際には0.0300を加算しています。
先ほどのグラフからは、この損失関数では、勾配は最小値に近づくほどに緩くなり、最小値から遠ざかるほどにきつくなることが分かります。そして、勾配と学習率を乗じた値を加算/減算することから、勾配がゼロになる地点よりも離れたところでは、重みの変化は大きくなり、勾配がゼロに近づくに従って重みの変化が少なくなることにも注意してください。
これに対して、学習率はいわば学習(パラメーターの更新)をどのくらいのスピードで進めるかを決定するファクタです。小さすぎる値を指定すると、勾配が大きな場合でも、いつまで経っても学習が進まず、逆に大きすぎる値を指定すると、勾配が小さな時でも、重みの変化量が大きくなりすぎて、適切な値が見つからないといった状況を招くこともあります。そのため、適当な値を指定する必要がありますが、これにはその場その場での試行錯誤が必要になるかもしれません。
最後に、同じ工程をもう一度だけ実行してみます。
print(w.grad)
optimizer.zero_grad()
print(w.grad)
y = f(x)
print(y)
loss = criterion(y, t)
loss.backward()
print('updated w.grad:', w.grad)
optimizer.step()
print('updated w:', w)
最初に行っているのは、勾配(w.grad属性)をリセットする処理です。grad属性に記録された勾配は、リセットをしない限り、累積されていくようになっていますが、これをゼロにして、学習ごとの勾配だけを使うようにしています。
その後は、これまでに見たコードそのままです。途中と最後には勾配の値と更新後の重みを表示するコードも含めてあります。
実行結果は次の通りです。
重みの値が理想値である2.0にまた少し近づいたことが分かります。また、勾配の値は0.04です。これと学習率の0.3を乗じると「0.012」が得られます。これと前回の重み「1.98」を加算した結果「1.992」が新しい重みの値となっている点にも注意してください。
後はこの作業を繰り返し実行していくことで、重みが2.0に近づいていくはずです。これについてはコードを示しませんが、冒頭に示したようにループ処理を書くことで必要なだけ学習を行えるはずです。
今回は学習の過程で、重みがどのようにして更新されていくかを見ました。ここまでであやめの品種を分類するニューラルネットワークのコードがどうしてあのようになっていたかはおおよそ説明し終わりました。最後に残ったのは、全結合を行うクラスです。次回は、これを行うクラスを簡易的に実装してみる予定です。
Copyright© Digital Advantage Corp. All Rights Reserved.

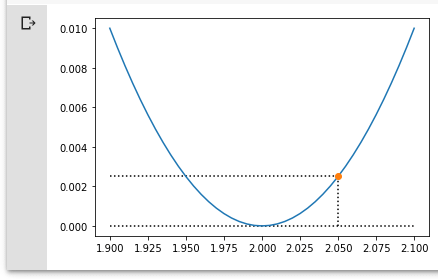 重みを2.05まで増やすと、その計算結果(2.05×1)は2.05となる
重みを2.05まで増やすと、その計算結果(2.05×1)は2.05となる 実行結果
実行結果 実行結果
実行結果 実行結果
実行結果 実行結果
実行結果



