ニューラルネットワークの学習でしていること:作って試そう! ディープラーニング工作室(1/2 ページ)
シンプルな関数をニューラルネットワークに見立てて、その係数を学習させながら、その過程でどんなことが行われているかを見ていきます。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は、ニューラルネットワークが何らかの値を推測するのに必要な重みやバイアスがどこにあるのか、それらを使ってどんなふうに計算が行われるのかを見ました。今回は、重みを例に、学習の過程でこれがどのようにして新しい値に更新されていくかを見てみます。
学習とは?
第2回では、次のようなコードで学習を行っていました。
net = Net() # ニューラルネットワークのインスタンスを生成
criterion = nn.MSELoss() # 損失関数
optimizer = torch.optim.SGD(net.parameters(), lr=0.003) # 最適化アルゴリズム
EPOCHS = 2000 # 2000回繰り返す
for epoch in range(EPOCHS):
optimizer.zero_grad() # 手順0:重みとバイアスの更新で内部的に使用するデータをリセット
outputs = net(X_train) # 手順1:ニューラルネットワークにデータを入力
loss = criterion(outputs, y_train) # 手順2:正解ラベルとの比較
loss.backward() # 手順3:誤差逆伝播
optimizer.step() # 手順4:重みとバイアスの更新
if epoch % 100 == 99: # 100回繰り返すたびに損失を表示
print(f'epoch: {epoch+1:4}, loss: {loss.data}')
print('training finished')
まず自分が記述したニューラルネットワークを表すクラスのインスタンスを生成して、損失関数と呼ばれる関数、最適化アルゴリズムという重みとバイアスを更新するのに使用するアルゴリズムを選択しています。
ここでは、損失関数としてPyTorchが提供するMSELossクラス(torch.nn.MSELossクラス)のインスタンスを代入しています。これは、ある値と別の値の距離(誤差)の2乗を損失として表すものです。そして、最適化アルゴリズムには、同じくPyTorchが提供するSGDクラス(torch.optim.GSDクラス)のインスタンスを代入しています。SGDとは「stochastic gradient descent」(確率的勾配降下法)の略で、PyTorchでは損失関数や誤差逆伝播法などと組み合わせて、重みを最適な値に更新していくために使用します(本稿ではこれについては深くは触れません)。
その後は2000回のループで実際の学習に入ります。ループ回数を指定している変数EPOCHSの「EPOCH(S)」とは「時代」のような意味の語ですが、ここでは学習を行うひとまとまりの単位(この場合は、訓練データを使った一度の学習)のようなものだと考えるとよいでしょう。
ループの内部では次のようなことをしています。
- 手順0:重みとバイアスの更新で内部的に使用するデータのリセット
- 手順1:ニューラルネットワークへの訓練データの入力
- 手順2:ニューラルネットワークが計算した値と正解ラベルを比較して、損失を計算
- 手順3:誤差逆伝播法により、重みとバイアスの更新に内部で使用するデータを計算
- 手順4:選択した最適化アルゴリズムを使用して、重みとバイアスを更新
このうちの手順1、つまりニューラルネットワークへの訓練データの入力については、これまでにも何度も見ています。今回はその後(とそれに付随する手順0)について、そこでどんなことが行われているのかを、手を動かしながら、簡単に見ていくことにします。
今回学習させるもの
今回はニューラルネットワーククラスを定義したりはしません。シンプルに重みは1つだけで、バイアスはなし、入力も1つだけとします。つまり、これは「y = w × x」という式で表せます。この重みがどのようにして更新されていくかをみることで、学習時にはどんなことが行われているかが想像できるようになるはずです。
実際には、重み(w)の初期値は1.95、それに対応する正解ラベルの値は2.0であるとします。つまり、「f(x) = 1.95 × x」という式が「f(x) = 2.0 × x」へと更新されていく過程を(最初の部分だけ)見ていきます。ここでは、xの値を1とします。つまり、f(x)の出力は1.95となりますが、実際には2.0になってほしいということです。
今述べたことをコードで表現すると次のようになります(変数wに代入している重みを表すテンソルのインスタンス生成で指定している「requires_grad=True」については後述します。今はそういうものだと思っておいてください)。なお、今回のコードはこのリンク先で公開しています。
import torch
w = torch.tensor([[1.95]], requires_grad=True) # 重みの初期値は1.95とする
t = torch.tensor([[2.0]]) # 重みの正解は2.0
x = torch.tensor([1.0]) # 関数への入力は1.0とする
def f(x): # 関数f(x) = w * xの定義
return w * x
print('w:', w)
print('t:', t)
関数f(x)をニューラルネットワークと見なせば、これは入力層と出力層のみで構成され、上の計算を行うニューラルネットワークのようにも考えられることに気が付いたでしょうか(ただし、今回はバイアスbを省略したと考えてください)。それっぽくするために、上に示した変数wは「1行1列の行列」(1行1列の2次元配列)として定義しています。変数xも「1要素のベクトル」(1要素の1次元配列)となっています(正解ラベルに相当する変数tは、以下で損失を計算する際に都合がよいように変数wと同じ形式としています)。
この後は、重みがどのように更新されていくかを観察していくことにしましょう。
損失の計算
これまでの連載の中でも述べていますが、ここで見ている(教師あり学習における)ニューラルネットワークの学習とは「損失を最小とするように、重みとバイアスを更新していく」過程のことです。損失とは、ニューラルネットワークが算出した出力値(推測値)と正解ラベルの値との誤差(距離)のことです。これが最小になるのは、出力値と正解ラベルが等しくなったときです。まずはこのことを頭に入れておきましょう。以下では損失の求め方について見ていきます(上記の手順2に相当)。
損失(誤差、距離)を計算するには幾つかの方法があります。ここでは、PyTorchが提供するMSELossクラス(torch.nn.MSELossクラス)を使用することにします。
MSEとは「Mean Squared Error」の略で、日本語にすると「平均二乗誤差」です。MSEでは、同じ要素数のベクトル(一次元配列)が2つあったときに、同じインデックス位置にある2つの要素で減算を行った結果を二乗したものを、それらの要素の誤差(二乗誤差)として考え、ベクトルの全要素についてそれらを計算し、それらの総和を要素数で割った値(平均値)を求めます。
今回の例では、比べるのは1つの出力値と1つの正解ラベルだけなので、平均の取りようがないのですが、これを使って話を進めることにしましょう。
ここで比較する対象(誤差を計算する2つの要素)は、関数f(x)の値と、正解ラベルです。変数xの値をここでは1とすることは既に述べました。よって、重みの初期値とした1.95と、変数xの値である1を乗じた結果である1.95と、正解ラベルの値である2の差である-0.05(または0.05)を二乗した0.0025が今回求める誤差となります。
実際にそうなるかを調べてみましょう。
criterion = torch.nn.MSELoss()
y = f(x)
loss = criterion(y, t)
print(loss.data)
ここでは、MSELossクラスのインスタンスを生成して、それを変数criterionに代入することで、損失関数を作成しています(「criterion」とは「何かをするときの基準や尺度」といった意味です。この場合、この後に行う重みの更新で実際にどんな処理をするかの判断基準になるといった意味でしょう)。後は、関数f(x)を呼び出して、その値と正解ラベルの値をcriterionに渡すことで損失を計算しています。
実行結果を以下に示します。
このような計算を実際に行う関数を自分で定義するとしたら、次のようになるでしょう(mycriterion関数はベクトルを受け取ることを前提としています。「1」のような配列以外の値を与えると例外が発生します)。
def mycriterion(x, y):
result = (x - y) ** 2
return result.sum() / len(result)
実際に、この関数を使ってみると、上のコードは次のようにも書けます。
myloss = mycriterion(y, t)
print(myloss)
「損失」(または誤差や距離)をどのように定義するかによって、損失関数はさまざまな種類に分類されます。ここでは平均二乗誤差を例としましたが、いずれにせよ、損失関数ではニューラルネットワークから得た値と、正解ラベルとの誤差を何らかの方法で計算することと覚えておきましょう。
次は、この損失を基に重みを更新していく作業を見ていきます。
Copyright© Digital Advantage Corp. All Rights Reserved.

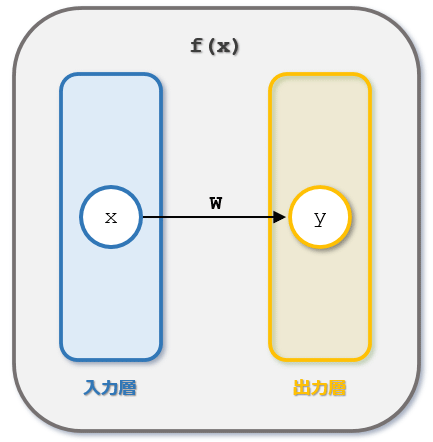 入力層のノード数が1、出力層のノード数が1、隠れ層がないニューラルネットワーク(のようなもの)
入力層のノード数が1、出力層のノード数が1、隠れ層がないニューラルネットワーク(のようなもの)
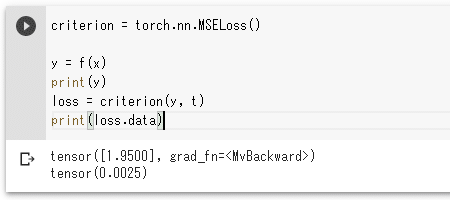 実行結果
実行結果



