[AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する:AI・機械学習の数学入門(2/2 ページ)
目標【その3】: 最小二乗法による回帰分析の超簡単な例
既にお話ししたように、回帰分析では各データの最も近くを通る回帰式の定数項と係数を求めます。そのためには「各データと回帰式のy方向の距離(誤差)の二乗の総和」を求め、それが最小になるように定数項と係数を決めればいいということでした(このような方法のことを「最小二乗法」と呼びます)。ここからは、実際にそういった計算をしていきます。
とはいえ、最初なのでできるだけ簡単な例にしましょう。目標その1で見た面積と家賃の例を使うことにします。面積が0なら家賃も0だと考えていいでしょうから、定数項は0とします。つまり、この単回帰分析の回帰式は、前のページで解説したy=b+axに当てはめると以下のようになります。
yが家賃、xが面積、aは係数です(bは0なので消えます)。簡単すぎますね。でも、最初から複雑な例に取り組もうとしても訳が分からなくなるだけなので、あえてここからスタートします。
答えを先に示しておきましょう。求めたい値は、各データを(x1,y1),(x2,y2), ... ,(xn,yn)で表したときに、各データと回帰式との間の誤差の二乗和が最小になるときのaの値です。aを求める式は最終的に、
となります。うひゃあ、簡単な例でもこんなに難しいの? と驚いた人もいるかもしれませんが、日本語で読み下せば恐るるに足らずです。
分子は「各データのxとyを掛けたものの総和」ですね。それを、分母の「xの二乗和」で割った値、ということになります。
具体例を当てはめると、分子は「各データの面積×家賃を総合計したもの」で、分母は「各データの面積の二乗を総合計したもの」です。
というわけで、式の計算内容(どういう計算なのか)は分かったと思います。謎なのは、どうやってこの式が導き出されるのかということですね。
今回の目標は、この式の計算内容が理解できること(もうできましたね)と、ちゃんと導き出せることです。一歩ずつ確実に進めていけば、必ずこの式にたどり着けるのでご心配なく。一緒に見ていきましょう。
解説:最小二乗法による回帰分析の超簡単な例(具体的な例)
いきなり、Σ満載の式をお見せしましたが、実感が湧くように、具体例を使って答えを導き出す流れを見ておきましょう(ここからの説明には動画も用意してあります)。
動画1 最小二乗法による回帰分析(具体的な例)
まず、図7(図1の再掲)の表から面積と家賃の最初(=表中の3行目)のデータを見てください。
最初のデータは面積xが18、家賃yが5です。もし、家賃が(前述のように)y=axで求められるなら、直線上の点のy座標は18aです。
図8の青い矢印がデータと直線との距離だということが分かりますね。従って、「実際のデータのy座標(5)」と「直線上のy座標(18a)」との距離の二乗は、以下の式で求められます。
ただし、aが先にあった方が計算が楽になるので、以下のように表すことにします。二乗すれば必ず正になるので、上の式を以下のように書き換えても結果は同じです。
他のデータについても、「実際のデータのy座標」と「直線上のy座標」との距離、つまり誤差の二乗は図9のように求められます。
私たちがやりたいことは、誤差の二乗和を最小にするaの値を求めることでしたね。そこで、まずはこれらの誤差の二乗和を求めてみましょう。誤差の二乗を全部足せばいいので、以下のようになります。
二乗の展開公式、つまり(a−b)2=a2−2ab+b2を使って、(1)式を展開しておきましょう。以下、確実に流れを追いかけられるように穴埋めにしてあります(説明を聞きながら流れを追いかけたい人は前掲の動画1を利用してみてください)。
(18a−5)2+(22a−9)2+(38a−15)2
=(18a)2− 2 ⋅ 18 ⋅ 5a + 5 2
+ (22a)2− 2 ⋅ 22 ⋅ 9a + 9 2
+ (38a)2− 2 ⋅ 38 ⋅ 15a + 15 2 ⋯
[A]
=(182+222+382)a2−2(18⋅5+22⋅9+38⋅15)a+(52+92+152) ⋯
[B]
[A] …… 二乗の展開の公式を適用した
[B] …… 次数の降順にまとめた
数値の計算は後回しにします。例えば、18 ⋅ 5などの計算は後でやるということです。もしかすると後で約分して式を簡単にできたりするかもしれません。また、微分すると定数項が消えるので、いちいち計算するのは無駄だというわけです(というわけで、次に微分を使うことがバレてしまいましたね)。
続けましょう。測定値の一番近くを通る直線を求めるには、誤差の二乗和を最小にするaの値を求めるといいということですね。ひと目見て分かると思いますが、上の式はaの二次式で、a2の係数は正です。グラフは下に凸な形になります。図10のような感じです。
このグラフを見れば、二次式が最小の値になるのは接線の傾きが0のときだということが分かりますね。接線の傾きはどうすれば求められたかというと……そう、前回やったとおり、微分すれば求められます*5。
*5 この連載の2回目で見たように、平方完成でも求められますね。ちなみに、二乗のことは「平方」とも呼ばれるので、誤差の二乗和は「誤差平方和」とも呼ばれます。
では、(1)式を展開したものをaで微分し、0と置いてみましょう。以下の式で、アンダーラインを引いた部分は定数なので、簡単に微分できます。
2 (182+222+382)a− 2 (18⋅5+22⋅9+38⋅15) = 0 ⋯
[B]
[A] …… 微分して0とおいた
[B] …… 微分の計算を行った
最初の項は{a2}'=2aを利用すれば求められます。また、2番目の項はa'=1を利用すれば求められます。定数項は消えてしまうので、ずいぶんと簡単になりましたね。B式はaについての簡単な方程式であることも分かります。あとは一気に解いていきましょう。
[B] …… 上の式(再掲)
[C] …… 移項した(2a−2b=0 → 2a=2bのようにした)
[D] …… 両辺を2で割った(2a=2b → a=bのようにした)
[E] …… 両辺を182+222+382で割って「a=○○」の形にした
[F]〜[H] …… 分母と分子を計算して、答えを求めた
というわけで、係数aの値が求められました。回帰式はy=0.381xということになります。最初に見たExcelでの例(図1)と一致していますね。
解説:最小二乗法による回帰分析の超簡単な例(一般的な例)
今度は、一般的な場合で考えてみましょう。いきなり文字式を使って計算していってもいいのですが、せっかく具体例を見たので、ちょっと「アタリ」を付けておきましょう。具体例のデータは以下のようなものでした。
| x(面積) | y(家賃) |
|---|---|
| 18 | 5 |
| 22 | 9 |
| 38 | 15 |
| 表1 面積と家賃のデータ | |
具体例の計算途中にあったE式を思い出してみてください(図11)。
この式の分母はxの各要素の二乗和ですね。分子はxの各要素とyの各要素を掛けたものの総和です。なので、
になりそうだ、ということが想像できます*6。
*6 計算練習って修行とか苦行のように思われますが、機械的に計算するのではなく、式の特徴や公式との関係を想像しながら進めると、一般的な式で考えるときにも実感が湧いてくると思います。
というわけで、本当にこうなるのかを次に見ていきます。動画でも解説しているので、ぜひ参照してみてください。
動画2 最小二乗法による回帰分析(一般的な場合)
各データを(x1,y1),(x2,y2), ... ,(xn,yn)で表したとします。今のところ、回帰式はy=axですね(図12)。まず、最初のデータについて考えます。実際のデータは(x1,y1)ですが、回帰式でのy座標はy=axのxにx1を代入した値になります。つまり、ax1ですね。
誤差の二乗は以下の式で求められます。
となります。他のデータについても同様ですね。誤差の二乗の総和は以下のようになります。
ですね。これを展開して、aについて整理しましょう。
[A] …… 二乗の展開公式を使って展開した
[B] …… Σを各項に分けた
[C] …… aについて整理した
C式への変形がちょっととまどうかもしれません。xiやyiはiによって異なる値となりますが、Σの計算から見ると2やaは定数なので、Σの外に出せます。
さて、aの係数は、xiの二乗和なので正です。そして、aの二乗の式になっているので、これは下に凸な二次関数のグラフになります。この式が最小になるのは接線の傾きが0のときなので、微分して0と置いてみましょう。今度はaを変数として扱います。
[A] …… 微分して0と置いた
[B] …… 微分の計算をした(aについての方程式になった)
[C] …… 移項して両辺を2で割った
[D] …… 両辺をΣxi2で割った
A式からB式に変形するときに、微分の線形性の公式を使って各項の計算をしているのに気づいたでしょうか(ごく自然にやっているので、意識に上らなかったかもしれませんね)。式が複雑になっても、ちゃんと公式の形に当てはまっていることが分かると思います。
いかがでしょう。ちゃんと目標のところで示した式になりましたね。メデタシメデタシです!
ところで、ここまでは回帰式がy=axという単純なものだったので、誤差の二乗和を微分して0と置くだけで係数aが求められました。しかし、定数項bがある場合(つまりy=b+axの場合)はどうすればいいのでしょうか。また、重回帰分析の場合、つまり説明変数がx1,x2,...とたくさんある場合にはどうすればいいのでしょうか*7。
*7 ここでのx1,x2,...は、変数xの1番目の要素、2番目の要素、……という意味ではありません。変数x1、変数x2、……という意味です。従って、変数x1の最初の要素はx11、次の要素はx12のように表されます。
実は、そのような場合には、偏微分と呼ばれる方法を使います。偏微分は高校の数学では出てこないかもしませんが、単に1つの変数に注目し、他の変数は定数として微分するだけのことです。例えば、回帰式がy=b+axの場合、上のように誤差の二乗和を求め、まずbで偏微分して0と置きます。次にaで偏微分して0と置きます。これで方程式が2つできる(aとbの連立方程式になる)ので、あとはそれを解くだけです。これは、変数が増えても同じことです。回帰式が、
であれば、a0、a1、a2についての連立方程式ができるので、それらを解くだけです。
しかし、一度に詰め込んでも消化しきれないでしょうから、今回は偏微分についてはちょっとお預けにしておきたいと思います(次回を楽しみにしていてください)。
次回は……
今回は微分の基本的な公式をおさらいした後、回帰分析への応用として最小二乗法の基本的な計算方法を見ました。回帰分析に関しては、定数項を求めたり、説明変数が増えたりすると偏微分が必要になります。偏微分については次回のお話で見ていくこととします。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

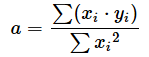
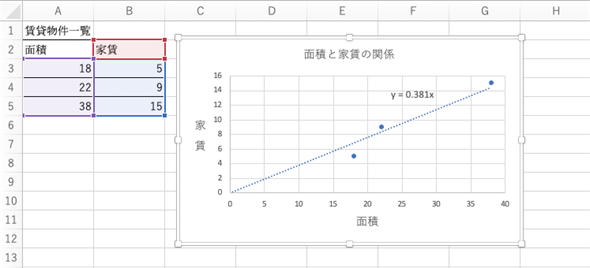
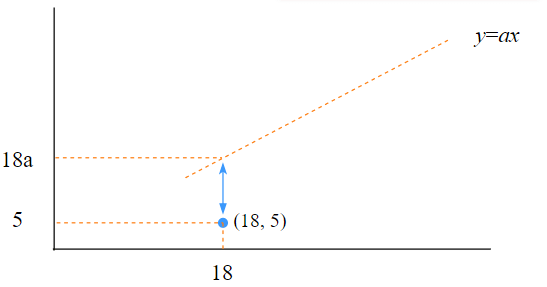 図8 測定値と回帰式(直線)との間の誤差
図8 測定値と回帰式(直線)との間の誤差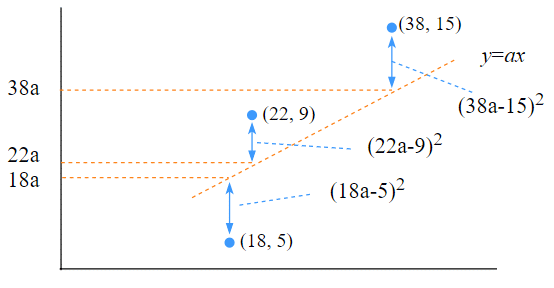 図9 測定値と回帰式(直線)との間の誤差の二乗を求める
図9 測定値と回帰式(直線)との間の誤差の二乗を求める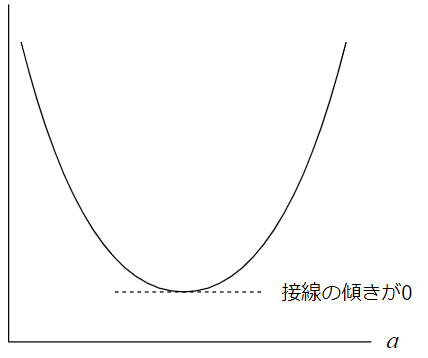 図10 下に凸な二次関数の値が最小になるのは接線の傾きが0になったとき
図10 下に凸な二次関数の値が最小になるのは接線の傾きが0になったとき


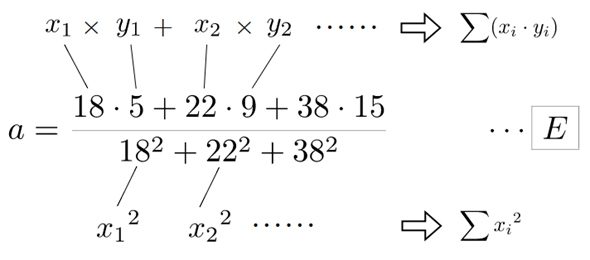


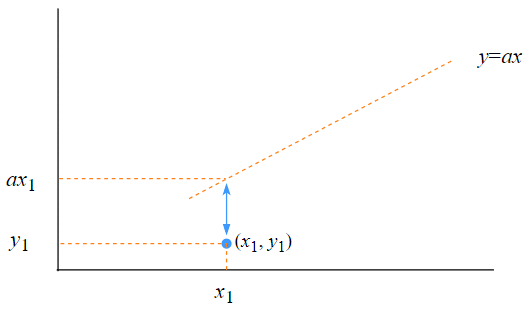 図12 各データと回帰式(直線)との間の誤差を求める
図12 各データと回帰式(直線)との間の誤差を求める






