[AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する:AI・機械学習の数学入門(1/2 ページ)
微分の考え方と計算方法を理解したら、次は微分の公式を押さえて活用してみよう。幾つかの公式を紹介し、応用例として回帰分析を行うための最小二乗法について基本的な考え方を見ていく。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
微分の考え方と計算方法については、前回、一通り見ました。微分は、最小値を求めたり、最適な値に近づけていったりする計算に使えるというお話はしましたが、具体例はまだ紹介していませんでした。
そこで、今回は、最小二乗法を利用して回帰分析を行う方法を紹介します。最初に少し微分の公式をおさらいしつつ整理しておき、続いて回帰分析の簡単な例へと進みます。
目標【その1】: 微分の公式を整理しておく
以下に示す公式は微分の計算をするときに必ず使う公式です*1。
*1 かっこが二重になって見づらいときには、外側のかっこを{}にして見やすくすることがあるよ。
公式(1)を日本語で読み下すと、
「関数のa倍を微分したものと、関数を微分したものをa倍したものと、が等しい」
という意味になります。
一方、公式(2)は、
「関数の和の微分は、関数の微分の和と等しい」
といった意味になります。これらの式は「微分の線形性」と呼ばれる性質を表したものです(※「線形性」の意味は後述します)。
さらに、公式(1)と公式(2)から、以下の公式(3)も導き出せます。
実は、これらの公式は直感的に理解できるので、これまで当然のように何度も使ってきました。微分の基本の基本でもあり、今回のテーマである最小二乗法を利用した回帰分析でも使うので、ここできちんと確認しておこうというわけです。
解説:微分の公式を整理しておく
目標のところに記した(1)(2)の公式については、極限(lim)に戻れば、簡単に証明できます。しかし、本筋のお話から外れるので証明は割愛し、ここでは公式の意味と具体例を確認するにとどめます。
まず、公式(1)の意味を見ると図1のようになります。
要するに、関数の定数倍は、微分の外に出せるということです。「元の関数に係数aが掛けられているときには、微分して係数aを掛けてもいい」ということですね。
ただし、公式(1)では、aが定数であることに注意してください。x・f(x)のように関数の中で使われている変数を掛けたものだと、この式は成り立ちません*2。
*2 そのような場合は、式を展開してから微分してください。例えばf(x)=2x2+1のときはxf(x) = x(2x2+1) = 2x3+xのように展開してから微分します。答えは6x2+1ですね。この計算には、微分の積の公式も使えますが、それについては回を改めて紹介します。
ここで、微分の基本的な計算方法について、ちょっと細かく見てみます。分かり切った話を回りくどく説明する感じになるので、面倒に感じたら公式(2)の説明まで読み飛ばしてもらって結構です。
さて、ちょっと細かな話です。そもそも、微分の最もシンプルな形(公式)は以下のような式です。計算方法は、(1)指数を係数に掛ける、(2)指数を1減らす、でしたね。
公式(1)と公式(0)を使えば、以下のような計算ができます。
[A] …… 公式(1)を適用してaを外に出した
[B] …… 公式(0)を適用してxnを微分した
これまで、しごく当たり前のように、
のような計算をしてきましたが、上で見たように、細かくステップを分けて公式を当てはめると以下のような計算になります。
[A] …… 公式(1)を適用して2を外に出した
[B] …… 公式(0)の公式を適用しでx3を微分した
続いて、公式(2)についても図2で確認しておきましょう。
これまで「多項式の場合は各項を微分すればいい」とお話してきましたが、この公式がそういった計算を行う根拠です。具体例で穴埋め問題を解きながら確認しておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
のとき、公式(2)の左辺は以下の通りになります。
{f(x)+g(x)}'
= {4x3 + 4x + 1 + 5x2 + 2x + 3}' ⋯
[A]
= ( 4 x3 + 5 x2 + 6 x + 4)' ⋯
[B]
= 12 x2 + 10 x + 6 ⋯
[C]
[A] …… f(x)とg(x)を当てはめた
[B] …… 次数の降順に整理した
[C] …… 各項の微分を計算した
計算は単なる掛け算と足し算だけなので難しくはないですね。何気なく式を変形して計算をしていますが、実をいうとC式への変形のところで、しれっと公式(2)そのものを使っています(各項を個別に微分していますよね)。ですが、まあ、ここは式の確認と計算練習ということで目をつむりましょう。
公式(2)の右辺にもf(x)とg(x)を当てはめてみます。
f'(x)+g'(x)
= (4x3 + 4x + 1)' + (5x2 + 2x + 3)' ⋯
[A]
= ( 3 ⋅ 4x2 + 4 ) + ( 2 ⋅ 5x+ 2 ) ⋯
[B]
= 12 x2 + 10 x + 6 ⋯
[C]
[A] …… f(x)とg(x)を当てはめた
[B] …… 各項の微分を計算した
[C] …… 次数の降順に整理した
正しく計算できていれば、左辺の結果と右辺の結果が一致するはずです(毎度のことですが、これは証明ではなく、1つの例で単に答えが合うことを確認しただけです)。
さて、目標のところに記したように、これらの公式は「微分の線形性」を表しています。
「線形性」というのは、公式(1)と公式(2)のような性質が成り立つことを言います(まとめて言えば公式(3)のような性質が成り立つことです)。つまり、
(1)「項を何倍かしたものに何らかの計算をしたもの」と「項に何らかの計算をしたものを何倍かしたもの」が等しくなる
(2)「各項を足したものに対して何らかの計算(例えば微分)をしたもの」と「何らかの計算(微分)を個々の項にしたものを足したもの」とが等しくなる
という性質と考えればいいでしょう。今回は「何らかの計算」は「微分」でしたが、極限(lim)や総和(Σ)に関しても線形性が成り立ちます。
ちなみに、公式(3)は以下のように導き出せます。公式(3)の記述とは逆に、右辺から左辺を導き出していきますね。
[A] …… 公式(1)を逆に適用してaとbを微分の中に入れた
[B] …… 公式(2)を逆に適用して個々の微分をまとめた
公式(3)式は、公式(2)に定数aとbを掛けただけなので、さほど理解に苦しむことはないと思います。
さらに、微分の計算をしっかりと身に付けるための練習問題を以下に用意しておきますが、早く回帰分析をやってみたい、という人は練習問題を飛ばして次に進んでもらっても構いません。
練習問題
(1)微分の公式を書いてみましょう
{a ⋅ f(x)+b ⋅ g(x)}' = a ⋅ f'(x) + b ⋅ g'(x) (a, bは定数)
(2)以下の計算を行ってみましょう
のとき、(1)で書いた公式のaに当たる値を3、bに当たる値を2とします。このとき、公式の左辺での計算と右辺での計算をやってみてください。
左辺は以下の通りです。
{a ⋅ f(x)+b ⋅ g(x)}'
= { 3 ⋅ (x3 − 2x2 + 1) + 2 ⋅ (5x2 + x + 3)}' ⋯
[A]
= ( 3 x3 − 6 x2 + 3 + 10 x2 + 2 x + 6 )' ⋯
[B]
= ( 3 x3 + 4 x2 + 2 x + 9 )' ⋯
[C]
= 9 x2 + 8 x + 2 ⋯
[D]
[A] …… aに3を代入し、bに2を代入した
[B] …… 3と2を分配して式を展開した
[C] …… 次数の降順に項をまとめた
[D] …… 微分した
右辺は以下の通りです。
af'(x) + bf'(x)
= 3 (x3 − 2x2 + 1)' + 2 (5x2 + x + 3)' ⋯
[A]
= 3 ( 3 x2 − 4 x) + 2 ( 10 x + 1 ) ⋯
[B]
= 9 x2 − 12 x + 20 x + 2 ⋯
[C]
= 9 x2 + 8 x + 2 ⋯
[D]
[A] …… aに3を代入し、bに2を代入した
[B] …… 各項を微分した
[C] …… 3と2を分配して式を展開した
[D] …… 次数の降順に項をまとめた
目標【その2】: 回帰分析とは何かを知る
では、微分の応用例として回帰分析への適用について見てみましょう。まず、回帰分析とは何かを簡単に説明しておきます。回帰分析とは、データを何らかの式に当てはめること、と考えていいでしょう。そのような式のことを回帰式と呼びます。回帰式としては、直線の式が最も単純な例です。例えば、賃貸住宅の面積と家賃が直線的な関係になっているものとしましょう。このとき回帰式(直線の式)は、
となります。
この場合、面積がx、家賃がyに当たることが分かりますね。aは係数(直線の傾き)、bは定数項(切片、つまりx=0のときのyの値)です。
回帰分析は表計算ソフト「Excel」などでも簡単にできます。
図3では、セルA3には18、セルB3には5という値が入っていますが、これは面積が18m2の物件の家賃が5万円だという意味です。同様に、22m2の物件なら9万円、38m2の物件なら15万円という3つのデータがありますね。グラフはそれらのデータを基に作った散布図です。散布図では、回帰式を表す直線やその式を表示できるので、併せて示してあります。
グラフの中にも記されているように、回帰式の係数aは0.381となっていることが分かります(ここでは、定数項のbは0として計算しています)。また、回帰式が分かれば、元のデータにはなかった面積の物件でも、家賃が予測できることが分かりますね。例えば、面積が30m2なら、家賃は0.381×30=11.43万円と予測できます。
なんだ、Excelで求められるのなら別に微分の話とか、機械学習の話とかは知らなくてもコトは足りるんじゃないの、と思われるかもしれません。しかし、回帰式が複雑になるとExcelで計算するのが難しい場合もあります。そのような状況を考えると、どのような仕組みで定数項や係数が求められるのかを知っておくことは重要です。式さえ立てられれば、あとはコンピュータ(統計パッケージやプログラムなど)に計算させればいいというわけです。
解説:回帰分析とは何かを知る
回帰分析の方法は、ズバリ、測定されたデータの最も近くを通る回帰式を求める、という方法です。回帰式が直線の場合は、もちろん直線の式y=ax+b(のaとb)を求めるわけです。
ところで、「最も近くを通る」というのはどういうことでしょうか。図4で考えてみましょう。
データの近くを通りそうな直線をざっくりと引いてみましたが、図4の上のグラフでは直線があまりデータの近くを通ってはいないようです。一方、下のグラフはデータの近くを通っていそうですね。図からも想像が付くと思いますが、「最も近くを通る回帰式(直線の式)を求める」というのは、各データと直線の距離の二乗和が最も小さくなるように、傾きaを決めるということです*3。
*3 一般に「距離」というとユークリッド距離のことを表すので、各点から直線に引いた垂線の長さが距離となりますが、ここで「距離」と呼んでいるのはy方向の距離のことです。これは、実際の値と、y=axという式に従うならこうなるはずだという理論的な値との差なので、「誤差」と考えられますね。従って、これ以降は「誤差」と呼ぶことにします。
単なる和ではなく二乗和を使う理由は連載の第2回でお話しました。単なる和だとプラスとマイナスで相殺されてしまうから、ですね。また、絶対値の和だと、
が1つに決まらないこともあるので、二乗和を使う、ということでした。
そうと分かれば、さっそく回帰式を求めてみたいと思うのが人情ですが、その前にもう少しだけ回帰分析について説明しておきます。その方が意味合いもよく分かりますし、先を見通すこともできるので。
既にお気づきかもしれませんが、当然のことながら、家賃は面積だけで決まるわけではありません。築年数や駅からの距離、階数などによっても変わるでしょう。そういうわけで、xに当たる変数が複数ある場合もあります。すると、直線ではなく平面やさらにそれ以上の次元(超平面)の、ちょっと図では表しにくい式になります。図5はxに当たる変数が2つある場合のイメージで、回帰式はこのような3次元空間の平面で表現できます。
このとき、軸を表す文字をたくさん使うのはわずらわしいので、添字を使って変数を区別するのが普通です。例えば、上の「家賃計算」の例では、家賃をy、面積をx1、築年数をx2、駅からの距離をx3のように表します(係数や定数項も添字で区別します)。x1やx2、x3によってyを説明するので、これらの変数のことを説明変数と呼びます。一方、説明される方のyは目的変数と呼ばれます。また、説明変数が1つの場合の回帰分析のことを単回帰分析、説明変数が複数の場合の回帰分析のことを重回帰分析と呼びます*4。
*4 目的変数は「従属変数」、説明変数は「独立変数」などとも呼ばれます。
新しい用語がたくさん出てきたので、ちょっとまとめておきましょう。図6の式が回帰分析で使われる回帰式の例です。ここでは、項の順序を変えて、定数項を最初に書いてあります。
単回帰にしろ重回帰にしろ、与えられたデータを基に回帰式の定数項や係数を求めることに変わりはありません。重回帰の場合、定数項や係数がたくさんある、というだけのことです。ここでは定数項や係数をaiという文字で表していますが、機械学習では、定数項や係数をwiやθiという文字で表すことがあります。wは重み(weight)の略です。θは角度を表すのにも使われますが、パラメータ(何かを特徴付ける値など)を表すときにも使われます。なお、ここでは全ての項が一次式である場合の例を示していますが、二次の項(xi2)などを含めた方が、当てはまりのいい場合も考えられます。
次のページは……
次のページでは、最小二乗法による回帰分析の計算を実際にしていきます。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

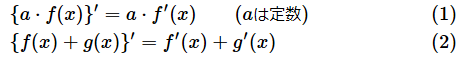

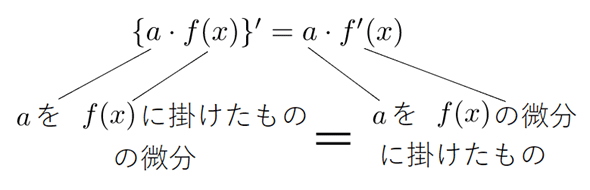
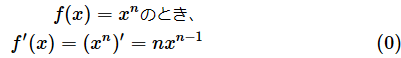
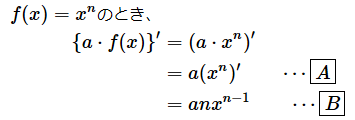
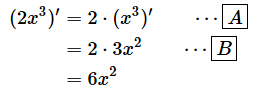
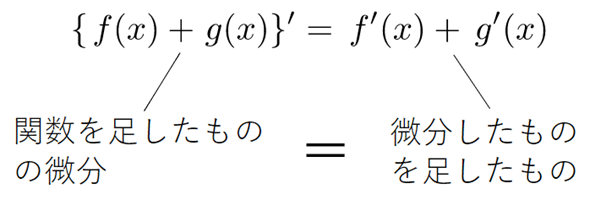
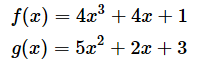
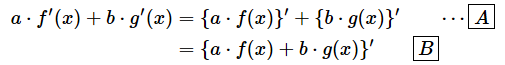
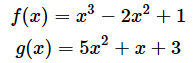
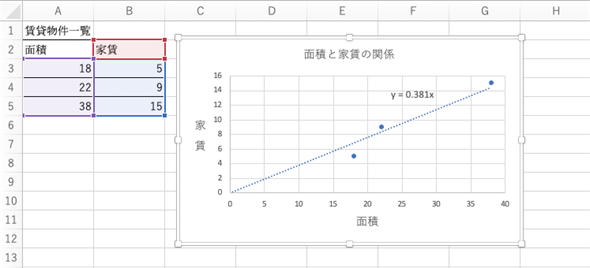
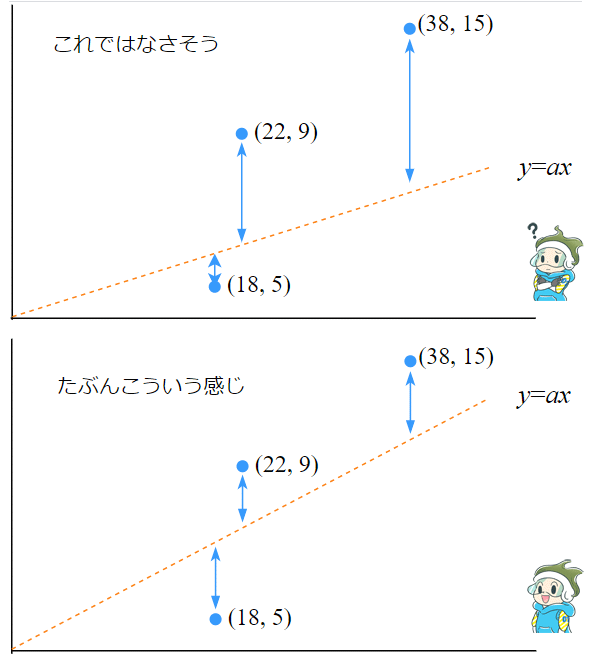 図4 データの最も近くを通る直線を探す
図4 データの最も近くを通る直線を探す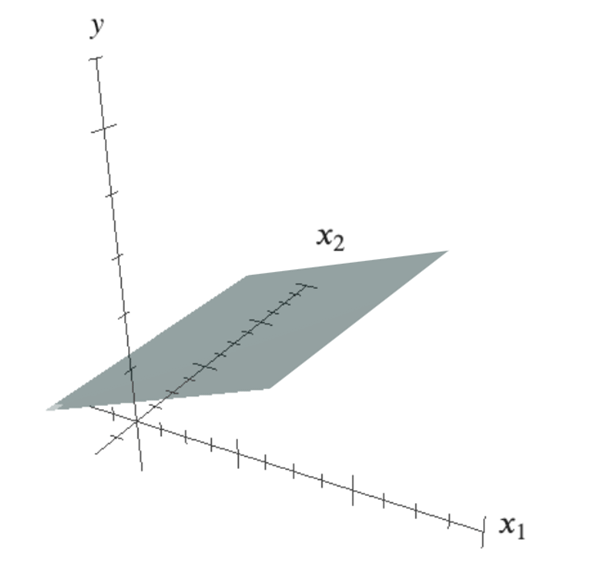
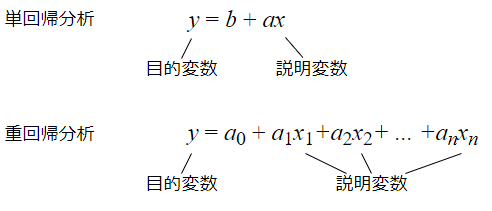 図6 単回帰分析と重回帰分析の回帰式
図6 単回帰分析と重回帰分析の回帰式



