みにくいアヒルの子の定理（Ugly Duckling theorem）とは？：AI・機械学習の用語辞典
用語「みにくいアヒルの子の定理（Ugly Duckling theorem）」について説明。何らかの仮定／前提知識がないと、分類やパターン認識は不可能であることを指す。
用語解説
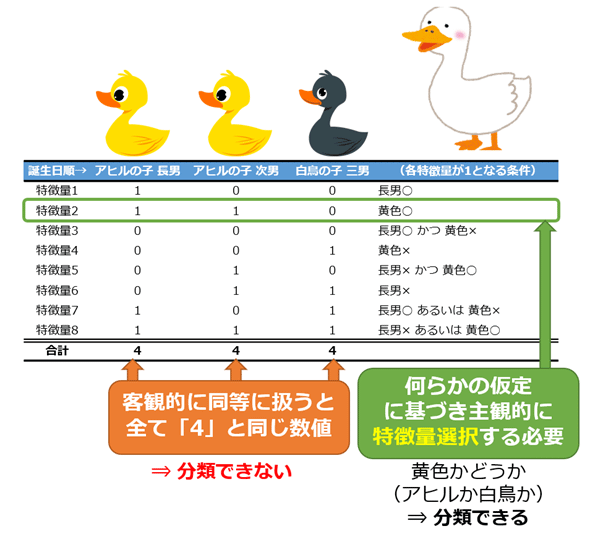
機械学習におけるみにくいアヒルの子の定理（醜いアヒルの子の定理： Ugly Duckling theorem）とは、何らかの「仮定（＝事前知識や偏向、帰納バイアス）」がないと「分類（＝類似性の判断）」は（理論上）不可能である、ということを主張する定理である。つまり分類やパターン認識において、あらゆる特徴量を客観的に同等に扱うことはできず、何らかの仮定に基づいて主観的に特徴量選択を行うことが本質的に必要であることを示す。
概念的にはノーフリーランチ定理に似ており、機械学習で必修の定理として一緒に学ぶことが多い。ノーフリーランチ定理は「あらゆる問題を効率よく解けるような“万能”の機械学習モデルや探索／最適化のアルゴリズムなどは存在しない」ことを主張する用語である。一方、みにくいアヒルの子の定理は「仮定／事前知識がない場合には、分類性能が高くなるような“最良”の特徴表現／特徴量セットも存在しない」ことを主張する。分類における「類似性」という単純な概念でさえ、基本的には問題領域における暗黙の仮定（何らかの事前知識や偏向）に依存しているということである。
提唱者による1973年の論文の一節を引用すると（※引用文章の「プレディケート」は「述語」という意味で、機械学習における「特徴量／特徴」に相当するものと考えられる）、
コンピュータの場合に我々がこれとこれのプレディケートが重要だということを教えてやれば, その後は確かにコンピュータで分類ができる. しかしその重要なプレディケートをどうして選ぶかという問題になると, 人間の場合には人間の目的によって決めてゆく. 我々の価値判断に依存している. コンピュータに価値判断がない限り, こういうものはいつまでも人間からコンピュータに教えてやらなければならないということがわかります.
と説明されている（※引用文献：「渡辺 慧, "人工知能の可能性と限界" 計測と制御 12 巻, 8 号 pp.675-687,1973.」における、683ページ目の「5. 概念」）。
ここまで少し堅苦しい説明となっているので、例え話を使ってより直感的に説明しておこう。
「みにくいアヒルの子の定理」の直感的な説明
この定理は、アンデルセン童話で有名なHans Christian Andersen氏が1843年に発表した代表作『みにくいアヒルの子』にちなんで名付けられたもので（詳細は上記論文のリンク先を参照）、理論物理学者の渡辺慧（Satoshi Watanabe）氏が1969年に著した書籍『Knowing and Guessing: A Quantitative Study of Inference and Information』の中で提示した。
ご存じの通り『みにくいアヒルの子』は、アヒルの子の群れの中に1羽だけ灰色の子がいて、「醜い」といじめに遭うが、大人になると美しい白鳥へと成長するストーリーである（詳しい内容はこちらのサイトがお勧め）。この定理では、客観的（＝数学的）に見ると「アヒルの子」と「白鳥の子」は、最終的に「アヒルの子」同士と同じくらい類似していることになる（つまり分類できない）と主張しているのである。
「いやいや、何を言っているの？ アヒルの子は黄色、白鳥の子は灰色、しかも鳥の種類も違うし、違う特徴を持っていますよね？」と思ったならば、それは主観的に見ていることになる。その分類を行った前提知識（暗黙の仮定）として、色や鳥の種類といった特徴量が主観的に選択されているからだ。
そこで例えば「アヒルの子たち」と「白鳥の子」に「黄色の船」を加えてみよう。そうすると、「アヒルの子」と「黄色の船」は、黄色、水上に浮かぶという同じ特徴を有しているので、類似性があるということになる。つまり「アヒルの子たち」と「白鳥の子」の類似性と、「アヒルの子」と「黄色の船」の類似性は同等ということになるだろう。「いやいや、鳥と船では全く違うよね？」と思ったならば、それも生物かどうかといった前提知識（暗黙の仮定）がやはり存在しているはずだ。
このように主観／前提知識（暗黙の仮定）を排除して分類することは不可能なのである。これを渡辺氏は数学的にも証明している。なお、その数学的な意味や証明については本稿では説明を割愛する。
Copyright© Digital Advantage Corp. All Rights Reserved.
注目のテーマ
ITmediaはアイティメディア株式会社の登録商標です。