コサイン類似度（Cosine Similarity）とは？：AI・機械学習の用語辞典

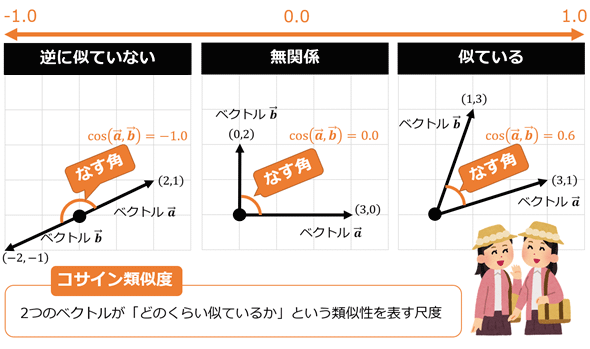
用語「コサイン類似度」について説明。2つのベクトルが「どのくらい似ているか」という類似性を表す尺度で、具体的には2つのベクトルがなす角のコサイン値のこと。1なら「似ている」を、-1なら「似ていない」を意味する。主に文書同士の類似性を評価するために使われている。

» 2024年09月09日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　数学／統計学／機械学習におけるコサイン類似度（Cosine Similarity）とは、2つのベクトルが「どのくらい似ているか」という類似性を表す尺度で、具体的には（ベクトル空間における）2つのベクトルがなす角のコサイン値のことである。この値は、2つのベクトルの内積（＝向きと大きさを持つベクトル同士の掛け算）を、2つのベクトルの大きさ（＝L₂ノルム）で割ることで計算される。

　この計算によって値が-1～1の範囲に正規化されるので、コサイン類似度が、

1なら「0度で、同じ向きのベクトル＝完全に似ている」
0なら「90度で、独立／直交した向きのベクトル＝似ている／いない、のどちらにも無関係」
-1なら「180度で、反対向きのベクトル＝完全に似ていない」

という意味になる（図1）。

図1　コサイン類似度のイメージ

定義と数式

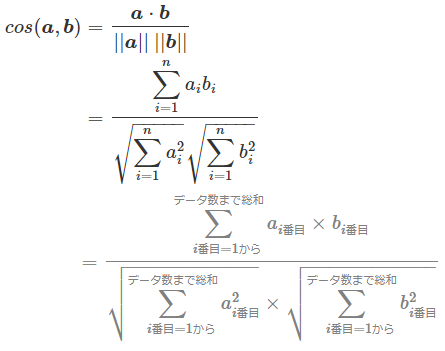
　この2つのベクトルのコサイン類似度、すなわち「この2つのベクトルがなす角θのコサイン値」（cosθ、cos(a,b)）を求める数式は、（高校で学ぶ）「2つのベクトル同士の内積の公式」から導き出せる。以下の1行目がその公式である。なお、|＜ベクトル＞|という数学記号は、「ベクトルの大きさ」を表す。

　2行目にある||＜ベクトル＞||という数学記号は、ベクトル空間における「長さ／距離」を表現する概念であるノルム（norm）を意味する。この公式におけるノルムは厳密には、ユークリッド距離であるL₂ノルムを意味する。

　ちなみに、ベクトルのaやbについて、1行目では高校数学風に→で書いたが、2行目では大学数学風に太字で記載した。いずれも同じベクトルを意味する。

　上記の公式をcos(a,b)=に変形すると、次のようになる。これがコサイン類似度の数式となる。

　ベクトルaやベクトルbは、例えば前掲の図1にある(1,3)のように2次元平面上のベクトルだけでなく、（図では表現できないが）例えば(1,2,3,4,5)のように5次元空間上のベクトルなど、

a=(a₁,a₂,...,a_n)
b=(b₁,b₂,...,b_n)

とn次元（＝多次元）空間上のベクトルに拡張することが可能である。

用途

　コサイン類似度は、主に2つの文章の類似性を評価するためによく使われている。文書同士のコサイン類似度は、文章を構成する単語群を数値群によるベクトルに置き換えることなどで計算できるようになる。

　例えばX（旧：Twitter）でポスト（旧：ツイート）をベクトルに置き換えることで、あるユーザーと他のユーザ－とのコサイン類似度を計算できるだろう。その数値を基に、あるユーザーのタイムライン上に、類似しているユーザーのポストを優先的に表示し、似ていないユーザーのポストをあまり表示しないようにすること（いわゆるレコメンデーションの一種）も実現できるだろう。

　コサイン類似度は、上記の例のようにレコメンデーションに応用したり、画像／動画でのポーズ推定に応用したりなど、さまざまな場面で活用できる可能性がある。ニューラルネットワークの損失関数や評価関数として使われることもある。近年では、広く普及し始めた大規模言語モデル（LLM）に関連して用いられることが増えており、コサイン類似度の知識はますます重要になってきている。

API

　主要ライブラリでコサイン類似度は、次のクラス／関数で定義されている。

scikit-learn： cosine_similarity関数
TensorFlow（2.x）／Keras：損失関数のCosineSimilarityクラスや評価関数のCosineSimilarityクラス、cosine_similarity()関数など
PyTorch： CosineSimilarityクラスやcosine_similarity()関数など

【応用】コサイン距離

　コサイン類似度を基にした距離尺度に「コサイン距離」がある。コサイン距離（Cosine distance）は、コサイン類似度の補数（1からコサイン類似度を引いた値： d＝1－cos(a,b)）を用いて、2つのベクトル間の相違度（＝距離）を示す。値が0に近いほどベクトルが類似しており、1に近いほど異なっていると判断できる。

　機械学習では、コサイン類似度が主に使用されているが、コサイン距離はコサイン類似度を補完する形で、ベクトル間の相違度を把握する際に参照されることがある。

「AI・機械学習の用語辞典」