正規化(Normalization)/標準化(Standardization)とは?:AI・機械学習の用語辞典
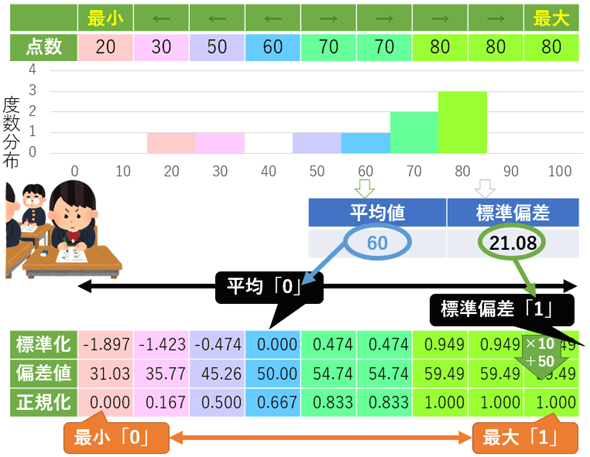
正規化とは、比較や分析を容易にするために、データの単位やスケールを共通の基準に整えること。単に「正規化」(Min-Max法)と言った場合は、データを最小値「0」〜最大値「1」にスケーリングすることを意味する。また、正規化の一種である標準化は、データを平均「0」、標準偏差「1」にスケーリングすることを意味する。
用語解説
一般的に正規化(Normalization)とは、さまざまな大きさや単位の情報/データを、比べやすく考えやすくするために、共通の基準やルールに合わせること、つまりデータを「普通の(Normal)」状態にする作業のことを指す。例えば走った距離を比較する際に、メートル(m)単位とキロメートル(km)単位が混在していると理解しづらいため、共通の単位に合わせる(例えば全てをkmに統一する)ことで情報が扱いやすくなる。
「正規化」や「標準化」という用語はさまざまな分野で用いられており、各分野で意味も異なる場合がある。例えばデータベース設計の「正規化」は、同じテーブル内のデータの重複をなくすなどの目的で、データを複数のテーブルに分割したりして整理することを指す。以下では「数学/統計学/機械学習における正規化」について説明している。
数学/統計学/機械学習における正規化(Normalization)とは、データのスケール(単位)を扱いやすいものに整えることである。正規化にはさまざまな方法が考えられるが、主要な方法に、
- 最小値0〜最大値1にスケーリングする「Min-Max normalization」
- 平均0、標準偏差1にスケーリングする「Z-score normalization」
の2つがある。
通常、単に「正規化」と言った場合は、Min-Max normalizationを指す。この場合の正規化とは、データの最小値からの偏差(=最小値を中心0にした場合の値)をデータ範囲(=最大値−最小値)で割ることである。これにより、データの最小値は0、最大値は1に変換される。
Z-score normalizationは、標準化(Standardization)と呼ばれるのが一般的である。標準化とは、データの平均値からの偏差(=平均値を中心0にした場合の値、中心化した値)を標準偏差で割ることである。これにより、データの平均は0、標準偏差(=データのバラツキ具合)は1に変換される(※なお、標準偏差1を二乗した「分散」の値も1なので、分散1とも表現できる)。ちなみに、標準化を応用したのが「偏差値」である(参考:用語辞典「分散/標準偏差」)。
用途と使い分け指針:正規化/標準化の違い
機械学習における正規化や標準化は、主に機械学習モデルに入力する前のデータに対して行われる。例えばデータの列(特徴量)によっては、その範囲が0〜1の場合もあれば、−50〜+5000の場合もあり得るが、このように列によって数値の範囲が違いすぎると機械学習がうまくできなかったり、学習により多くの時間がかかったりする可能性がある。よって多くの場合では、データの前処理として正規化/標準化を行った方がよい。
正規化(Min-Max法)は、特にデータの最小値と最大値の範囲が明確な場合に適した手法である。ただし、外れ値に敏感なため、大きい外れ値が存在する場合は標準化を使った方がよい。ちなみに、外れ値に対してよりロバスト(頑健)に正規化する方法の一つとして、データの中央値からの偏差(=中央値を中心0にした場合の値)を四分位範囲(=第3四分位数−第1四分位数)で割るRobustScalerもある。
標準化は、データの分布が正規分布(ガウス分布)に従っている場合に特に効果的な手法である。ただし、必ずしもデータの分布が正規分布でなくても使えるので、データの最小値と最大値の範囲が「不」明確な場合など、正規化(Min-Max法)があまり適切でないと考えられる場合にも標準化を用いるとよい。このため、正規化よりも標準化の方が使いやすいケースが多い。
また、機械学習モデルへの入力データの正規化/標準化(前処理)だけでなく、モデルからの出力結果のRMSE評価値を、正解(観測)データの平均値(もしくはデータ範囲や四分位範囲)で割って正規化したり、標準偏差で割って標準化したりすることもあり、正規化されたRMSE(Normalized RMSE:NRMSE)などと呼ばれる。NRMSEによって、スケールの異なるモデル間の性能を比較できるようになるというメリットがある。
「正規化(Min-Max法)」の定義と数式
正規化(Min-Max法)の数式は、以下のように定義できる。統計学に寄せて「観測値(observed value)」と表記したが、「実測値」「実際の測定値」の他、さまざまな方法で収集したデータがこの対象となる。
この定義は「i番目の観測値(つまり1つの値のみ)を正規化する式であること」に注意してほしい。データ全体を正規化するには、1番目からn番目までの各データを一つ一つ、この式を使って変換(=スケーリング)していく必要がある。
「標準化」の定義と数式
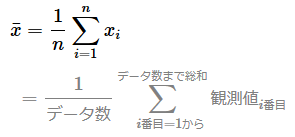
前提条件として、全データから平均値を計算する式は次のようになる。
また、前提条件として、全データの標準偏差を計算する式は次のようになる。
標準化の数式は、上記の平均値と標準偏差の式を使って以下のように定義できる。
先ほどの正規化と同様に、この定義は「i番目の観測値(つまり1つの値のみ)を標準化する式であること」に注意してほしい。
ここを更新しました(2024年4月8日)
2024年4月8日:標準化について、「平均0、分散1」という記述を、数式と同等の表現になるよう「平均0、標準偏差1」に書き直しました。
2024年3月4日:より多くの人が「正規化」の一般的な意味について理解できるように、分かりやすい表現へと書き直しました。データベース設計の「正規化」についての言及を追記しました。
Copyright© Digital Advantage Corp. All Rights Reserved.